Основная алгоритмическая структура Развилка

2. Уравнение прямых в общем виде:

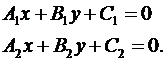
Условие перпендикулярности двух прямых записывается в виде

.

4. Квадрат можно описать окружностью, если диагональ квадрата меньше диаметра окружности или равна ему. Необходимо выразить диагональ квадрата и диаметр окружности через заданные площадь квадрата и длину окружности.

; L = pD

6. Две точки с координатами (x ₁, y ₁) и (x ₂, y ₂) лежат на одной окружности с центром в начале координат, если длины радиусов-векторов, соединяющих эти точки с началом координат, равны. Проверку на равенство осуществлять с заданной точностью. Длина радиус-вектора определяется как расстояние между двумя точками с координатами (0, 0) и (x, y).

Расстояние d от точки до начала координат определяется по формуле

.

8. Чтобы круг поместился в квадрат, диаметр круга должен быть меньше стороны квадрата или равен ей.

10. Точка с координатами (x, y) лежит на окружности радиуса R, если , где e – точность, с которой осуществляется проверка на равенство.

12. По трем сторонам с длинами a, b и c можно построить треугольник, если .При вводе длин сторон должно соблюдаться условие().

14. Точка с координатами (x, y) попадает в кольцо, если .

16. Окружность пересекает заданную, если выполняется неравенство: , где x, y – координаты центра второй окружности.

18. Необходимо выразить высоту h треугольника через его площадь s и основание b.

.

20. Уравнение прямых в общем виде:

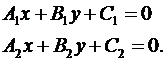
Условие параллельности двух прямых записывается в виде:

.

22. Условие, при котором три точки, заданные своими координатами (x ₁, y ₁), (x ₂, y ₂) и (x ₃, y ₃), лежат на одной прямой:

24. Треугольник называется равнобедренным, если равны две его стороны.

26. Треугольник называется прямоугольным, если значения длин его сторон удовлетворяют теореме Пифагора:

28. Треугольник называется правильным, если его углы равны.

30. Треугольник называется равносторонним, если все его стороны равны.

Не нашли, что искали? Воспользуйтесь поиском: