
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Последовательность расчета газового цикла
Обозначения и размерность величин, входящих в исходные данные, для выполнения домашнего задания приведены в таблице 1.3.
Таблица 1.3
Размерность исходных величин
для домашнего задания №2
| Наименование | Величины | Размерность |
| Начальное давление | р 1 | Н/м2 |
| Начальная температура | Т 1 | К |
| Давление после компрессора | р 2 | Н/м2 |
| Показатель политропы сжатия | п 1-2 | безразмерный |
| Температура газа после камеры сгорания | Т 3 | К |
| Показатель политропы в процессе подвода тепла к камере сгорания | п 2-3 | безразмерный |
| Давление за турбиной | р 4 | Н/м2 |
| Газовая постоянная рабочего тела | R | Дж/(кг*К) |
Газовая постоянная R определяется в зависимости от типа газа по таблице Приложения 1 или по формуле:
 ,
,
где µ - молекулярная масса газа.
Показатель адиабаты k вычисляется для каждого процесса по формуле:
 ,
,
а средние значения теплоемкости находятся для каждого процесса по формуле (1.19) с использованием данных таблиц Приложения 7. Для гелия можно принимать k =1,67 и считать k независимой от температуры газа.
Алгоритм расчета:
а) Вычисление термических параметров рабочего тела:
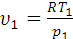 – удельный объем в начальном состоянии;
– удельный объем в начальном состоянии;
 – температура после сжатия в компрессоре;
– температура после сжатия в компрессоре;
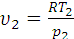 - удельный объем газа в точке 2;
- удельный объем газа в точке 2;
 – давление газа после камеры сгорания (точка 3);
– давление газа после камеры сгорания (точка 3);
 - удельный объем газа в точке 3;
- удельный объем газа в точке 3;
 – температура газа за турбиной (точка 4);
– температура газа за турбиной (точка 4);
 - удельный объем газа в точке 4;
- удельный объем газа в точке 4;
 – показатель политропы в процессе 4-1;
– показатель политропы в процессе 4-1;
б) теплота и работа процесса определяется из соотношений (1.30) и (1.31). Изменение энтальпии и внутренней энергии вычисляются по формулам:


а изменение энтропии – по формулам (1.41)-(1.43). Работа цикла определяется суммой работ расширения отдельных процессов, т.е.

Теплота, подводимая к рабочему телу в цикле q 1, находится как сумма теплот в процессах, где q 1>0.
Теплота цикла согласно (1.44): q n= q 1- q 2= I n.
Термический КПД цикла вычисляется по формуле (1.45).
В правильно выполненном расчете должны выполняться условия:

Пример. Произвести расчет замкнутого кругового процесса (цикла) с учетом зависимости теплоемкости  ,
,  и
и  от температуры газа в каждом процессе, из которых состоит цикл, если известно: рабочее тело – кислород (О2),
от температуры газа в каждом процессе, из которых состоит цикл, если известно: рабочее тело – кислород (О2),  , T 1=273 К, р 1=0,1 МПа, р 2=6*105 Па, п 1-2=1,45, T 3=1000 К, п 2-3=0,2, р 4=1,3*105 Па (см. рис. 1.1).
, T 1=273 К, р 1=0,1 МПа, р 2=6*105 Па, п 1-2=1,45, T 3=1000 К, п 2-3=0,2, р 4=1,3*105 Па (см. рис. 1.1).
Решение:
1. В соответствии с приведенным выше алгоритмом расчета вычислим параметры состояния рабочего тела в узловых точках цикла (т. 1, 2, 3, 4):





Для определения параметров газа в конце адиабатного расширения (точка 4) необходимо определит методом последовательных приближений показателей адиабаты  - среднее значение его для процесса 3-4. В качестве первого приближения значение k можно принять равным k 3-4=1,4 как для двухатомного газа. Для гелия и трехатомного газа можно принимать k =1,67 и k =1,33 соответственно.
- среднее значение его для процесса 3-4. В качестве первого приближения значение k можно принять равным k 3-4=1,4 как для двухатомного газа. Для гелия и трехатомного газа можно принимать k =1,67 и k =1,33 соответственно.
Тогда в первом приближении

Зная температуру начала и конца адиабатного расширения, необходимо определить среднее значение теплоемкостей для интервала температур (1000 - 681 К) с использованием таблиц Приложений 2 и 3, а также формулы (1.19).
Окончательно получаем
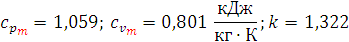
После этого принимаем за новое значение второго приближения k =1,322 и находим Т 4 =721 К и снова вычисляем, как указано выше, среднее значение теплоемкостей но уже для интервала температур (1000-721 К). Получаем:
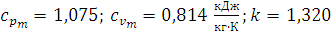 . Тогда уточненное значение Т 4=722,5 К.
. Тогда уточненное значение Т 4=722,5 К.
Удельный объем газа в конце адиабатного расширения находится как

Показатель политропы процесса 4 – 1:
r w:val="000000"/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:fareast="RU" w:bidi="RU"/></w:rPr><m:t>0.369</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
2. Вычислим работу расширения (сжатия) газа в политропных процессах по формулам (1.31):




Работа цикла находится как алгебраическая сумма работ процессов, составляющих цикл:
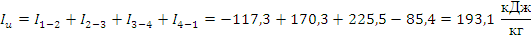
3. Вычислим теплоту для каждого политропного процесса по формуле:

где  - среднее значение теплоемкости в интервале температур
- среднее значение теплоемкости в интервале температур 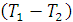
k - среднее значение показателя адиабаты в интервале 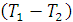
n - показатель политропы для процесса 1 – 2.
Так как для процесса сжатия в компрессоре  , то тепло в этом процессе подводится, а энтропия рабочего тела увеличивается. Средние значения теплоемкости находятся по методике, изложенной выше, с использованием таблиц Приложений 2 и 3.
, то тепло в этом процессе подводится, а энтропия рабочего тела увеличивается. Средние значения теплоемкости находятся по методике, изложенной выше, с использованием таблиц Приложений 2 и 3.
Для процесса 1 – 2 получаем окончательно
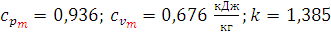
Тогда:

Для процесса подвода тепла (2 – 3) по изложенной методике находим:
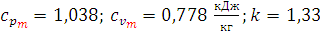

Аналогично находим и тепло (отведенное) процесса (4 – 1), в котором:


В процессе расширения (3 – 4) тепло не подводится (адиабатно), поэтому 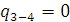 .
.
Известно, что разность подведенной и отведенной теплоты в цикле равна работе цикла. Вычислим эту разность:


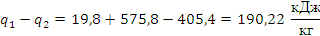
Относительная погрешность измерений будет равна

Термический КПД цикла находится как

4. Для проверки правильности расчетов можно вычислить изменение калорических параметров рабочего тела в каждом процессе цикла, т.е. ∆ i, ∆ u, ∆ s, где



где параметры с индексом «1» относятся к началу процесса, с индексом «2» - к концу процесса. Теплоемкости вычисляются как среднее для интервала температур 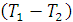 .
.
Результаты расчета сведены в табл.1.4.
Таблица 1.4
Итоговая таблица результатов расчетов
| Процессы | 1-2 | 2-3 | 3-4 | 4-1 |
| ∆ Т, К | -277,5 | -449,5 | ||

| 0,936 | 1,038 | 1,075 | 0,972 |

| 0,676 | 0,778 | 0,814 | 0,712 |
| k | 1,385 | 1,33 | 1,32 | 1,363 |

| 137,2 | 407,6 | -225,8 | -320 |

| -298,3 | -436,9 | ||

| 0,064 | 0,818 | 0,88 |
Сумма изменений калорических параметров должно равняться нулю в точно и правильно выполненных расчетах, т.е.

В рассмотренном примере получилось:



Таким образом, относительные погрешности вычислений в примере меньше 1%.
5. Для построения цикла в р -  –диаграмме необходимо вычислить удельный объем при среднеарифметическом значения давления для процесса (1-2) и (3-4).
–диаграмме необходимо вычислить удельный объем при среднеарифметическом значения давления для процесса (1-2) и (3-4).

- для процесса сжатия;

- для процесса расширения;
удельный объем υх находится из уравнения политропного процесса для процесса сжатия:

Аналогично и для процесса адиабатного расширения

Зная значения температур в узловых точках цикла и изменения энтропии в процессах, можно построить цикл в Т - s –диаграмме.
Не нашли, что искали? Воспользуйтесь поиском: