ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

1.3 Общие положения

При выполнении измерений результат всегда получается с некоторой погрешностью. Погрешностью измерений называют величину , определяемую из неравенства

,

(1)

где – истинное значение измеряемой величины, – измеренное значение величины.

Поскольку точное значение не известно, точно узнать нельзя. Поэтому указывают интервал , внутри которого с определенной вероятностью, называемой доверительной вероятностью, расположено значение . За лучшую оценку истинного значения результата измерений, принимают среднее арифметическое () из всех величин , полученных в процессе отдельных измерений, выполненных в одинаковых условиях:

(2)

где n – число отдельных измерений.

Качество результатов измерений бывает удобно характеризовать не абсолютной погрешностью , а ее отношением к найденному значению измеряемой величины , которое называют относительной погрешностью a и выражают в процентах:

(3)

Погрешности измерений принято подразделять на систематические, случайные и грубые.

Грубые погрешности (промахи) появляются из-за недостатка внимания экспериментатора. Грубая погрешность обычно существенно превышает случайную.

3.2 Систематические погрешности

Систематические погрешности δ вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Систематическую погрешность можно оценить, сравнив полученные результаты измерений с расчетным значением измеряемой величины, найденным на основании более точных экспериментальных данных, приведенных в справочнике.

3.3 Случайные погрешности

Случайные погрешности обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. Чаще всего случайные погрешности подчиняются нормальному закону распределения и могут быть оценены с помощью выборочной средней квадратической погрешности отдельного измерения ():

(4)

При большом числе измерений () можно утверждать, что точное значение измеряемой величины лежит в интервале с доверительной вероятностью 0.68 или в интервале с вероятностью 0.95.

Если для нахождения определенного значения физической величины проводят несколько (n) параллельных измерений, а затем по формуле (2) рассчитывают их среднее значение , то средняя квадратическая погрешность среднего арифметического будет меньше погрешности отдельного измерения в раз:

(5)

В предлагаемых лабораторных работах случайную погрешность измерений следует оценивать по формуле (4) на основании нескольких измерений (), выполненных в одинаковых условиях.

3.4 Учет систематической и случайной погрешностей

Часто бывает, что систематическая и случайная погрешности близки друг другу и обе определяют точность результата. Тогда можно найти суммарную погрешность , полагая, что систематической погрешности соответствует не бόльшая доверительная вероятность, чем утроенной среднеквадратической погрешности :

(6)

3.5 Погрешности косвенных измерений

Измерения подразделяются на прямые и косвенные. При прямом измерении искомую величину определяют непосредственно с помощью измерительного устройства, например находят высоту поднятия жидкости в манометре с помощью измерительной линейки. Результат косвенных измерений вычисляют по данным прямых измерений с помощью формул. Например, в работе № 1 средний тепловой эффект реакции находят по опытным данным с помощью формулы (см. приложение 2)

Погрешности прямых измерений могут быть найдены по соотношениям (3.4), (3.5) и (3.6). Если при косвенных измерениях интересующая нас величина является известной функцией других величин , которые измеряются непосредственно

(7)

то ее абсолютную погрешность можно найти как

(8)

где – абсолютная погрешность величины .

Лучшим приближением к истинному значению , как и в случае прямых измерений, считают среднее арифметическое значение .

Среднеарифметическое значение измеряемой величины и погрешность результата можно вычислить двумя способами:

1. Вычислить и, подставив эти значения в уравнение (3.7), найти . Затем, определив погрешности , по уравнению (3.8) найти .

2. Для каждой группы результатов совместных измерений (); (), …; (); …; () найти , затем рассчитать среднеарифметическое значение :

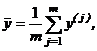
(9)

а погрешность определения величины вычислить обычным путем:

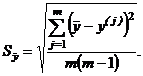
(10)

Систематическую погрешность косвенных измерений, как и прямых, можно оценить путем сравнения с результатами расчетов, выполненных с использованием справочных данных.

3.6 Требуемая точность вычислений. Целесообразное число значащих цифр в представлении результатов измерений

Во всех случаях нужно придерживаться следующего правила. Погрешность, получающаяся в результате вычислений, должна быть на порядок (т.е. в 10 раз) меньше суммарной погрешности измерений. При этом можно быть уверенным, что в процессе арифметических операций мы ощутимым образом не исказили результата.

Как окончательный результат вычислений записывают числа только с верными цифрами и одной сомнительной (так называется цифра того разряда, в котором содержится первая значащая цифра ошибки). Неверные цифры (правее сомнительной) отбрасывают с соблюдением правил округления. Следовательно, максимальная ошибка округления составит 5 единиц ближайшего отброшенного результата.

3.7 Оценка значимости изменения измеряемой величины

При выполнении предлагаемых лабораторных работ следует руководствоваться правилом: если изменение измеряемой величины превосходит утроенную среднеквадратичную погрешность, то это изменение значимо и является проявлением физико-химической закономерности. В противном случае обычно считают, что измеряемая величина изменялась под действием случайных факторов.

ТЕРМОДИНАМИКА

Не нашли, что искали? Воспользуйтесь поиском: