Тангенциальная составляющая ускорения 14 страница

Термодинамика дает метод расчета кривой равновесия двух фаз одного и того же вещества. Согласно уравнению Клапейрона — Клаузиуса, производная от равновесного давления по температуре равна

(76.1)

где L — теплота фазового перехода, (V ₂ —V ₁) — изменение объема вещества при пере­ходе его из первой фазы во вторую, Т — температура перехода (процесс изотермичес­кий).

Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равно­весия. Поскольку L и Т положительны, наклон задается знаком V ₂ —V ₁ . При испарении жидкостей и сублимации твердых тел объем вещества всегда возрастает, поэтому, согласно (76.1), d p /dT>0; следовательно, в этих процессах повышение температуры приводит к увеличению давления, и наоборот. При плавлении большинства веществ объем, как правило, возрастает, т. е. d p/ d T> 0; следовательно, увеличение давления приводит к повышению температуры плавления (сплошная КП на рис. 115). Для некоторых же веществ (Н₂О, Ge, чугун и др.) объем жидкой фазы меньше объема твердой фазы, т. е. d p /d T <0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рис. 115).

Диаграмма состояния, строящаяся на основе экспериментальных данных, позволя­ет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить при том или ином процессе. Например, при условиях, соответствующих точке 1 (рис. 116), вещество находится в твердом состоянии, точке 2 — в газообразном, а точке 3 — одновременно в жидком и газообразном состояниях. Допустим, что вещество в твердом состоянии, соответ­ствующем точке 4, подвергается изобарному нагреванию, изображенному на диаграм­ме состояния горизонтальной штриховой прямой 4—5—6. Из рисунка видно, что при температуре, соответствующей точке 5, вещество плавится, при более высокой тем­пературе, соответствующей точке 6, — начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагрева­нии (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жид­кость — кристаллическое состояние.

На диаграмме состояний (см. рис. 115 и 116) видно, что кривая испарения закан­чивается в критической точке К. Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересече­ния кривой испарения (переход 11—12 на рис. 116), т. е. такой переход, который не сопровождается фазовыми превращениями. Это возможно благодаря тому, что раз­личие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными). Переход же кристаллического состояния (харак­теризуется анизотропией) в жидкое или газообразное может быть только скачкообраз­ным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке. Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где p =0 и T =0 К.

Задачи

10.1. Углекислый газ массой m =1 кг находится при температуре 290 К в сосуде вместимостью 20 л. Определить давление газа, если: 1) газ реальный; 2) газ идеальный. Объяснить разли­чие в результатах. Поправки а и b принять равными соответственно 0,365 Н×м⁴моль² и 4,3×10^–5 м³/моль. [1) 2,44 МПа; 2) 2,76 МПа]

10.2. Кислород, содержащий количество вещества v =2 моль, занимает объем V ₁ = 1 л. Опреде­лить изменение D T температуры кислорода, если он адиабатически расширяется в вакуум до объема V ₂=10 л. Поправку а принять равной 0,136 Н×м⁴/моль². [—11,8 К]

10.3. Показать, что эффект Джоуля — Томсона всегда отрицателен, если дросселируется газ, си­лами притяжения молекул которого можно пренебречь.

10.4. Считая процесс образования мыльного пузыря изотермическим, определить работу А, кото­рую надо совершить, чтобы увеличить его диаметр от d ₁=2 см до d ₂=6 см. Поверхностное натяжение s мыльного раствора принять равным 40 мН/м. [0,8 мДж]

10.5. Воздушный пузырек диаметром d= 0,02 мм находится на глубине h =20 см под поверхностью воды. Определить давление воздуха в этом пузырьке. Атмосферное давление принять нор­мальным. Поверхностное натяжение воды s = 73 мН/м, а ее плотность r=1 г/см³ [118 кПа]

10.6. Вертикальный открытый капилляр внутренним диаметром d =3 мм опущен в сосуд с ртутью. Определить радиус кривизны ртутного мениска в капилляре, если разность уровней ртути в сосуде и в капилляре D h =3,7 мм. Плотность ртути r=13,6 г/см³, а поверхностное натяжение s = 0,5 Н/м. [2мм]

10.7. Для нагревания металлического шарика массой 25 г от 10 до 30°С затратили количество теплоты, равное 117 Дж. Определить теплоемкость шарика из закона Дюлонга и Пти и мате­риал шарика. [ М» 107 кг/моль; серебро]

3 ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ

Глава 11Электростатика

§ 77. Закон сохранения электрического заряда

Еще в глубокой древности было известно, что янтарь, потертый о шерсть, притягивает легкие предметы. Английский врач Джильберт (конец XVI в.) назвал тела, способные после натирания притягивать легкие предметы, наэлектризованными. Сейчас мы гово­рим, что тела при этом приобретают электрические заряды. Несмотря на огромное разнообразие веществ в природе, существует только два типа электрических зарядов: заряды, подобные возникающим на стекле, потертом о кожу (их назвали положитель­ными), и заряды, подобные возникающим на эбоните, потертом о мех (их назвали отрицательными), одноименные заряды друг от друга отталкиваются, разноимен­ные — притягиваются.

Опытным путем (1910—1914) американский физик Р. Милликен (1868—1953) пока­зал, что электрический заряд дискретен, т. е. заряд любого тела составляет целое кратное от элементарного электрического заряда е (е =1,6×10^–19 Кл). Электрон (m_e =9,11×10^–31 кг) и протон (т_p= 1,67×10^–27 кг) являются соответственно носителями элементарных отрицательного и положительного зарядов.

Все тела в природе способны электризоваться, т. е. приобретать электрический заряд. Электризация тел может осуществляться различными способами: соприкоснове­нием (трением), электростатической индукцией (см. § 92) и т. д. Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) — избыток отрицательного заряда. Общее количество зарядов обоих знаков, содержащихся в телах, не изменяется: эти заряды только перераспределяются между телами.

Из обобщения опытных данных был установлен фундаментальный закон природы, экспериментально подтвержденный в 1843 г. английским физиком М. Фарадеем (1791—1867), — закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними тела­ми) остается неизменной, какие бы процессы ни происходили внутри этой системы.

Электрический заряд — величина релятивистски инвариантная, т. е. не зависит от системы отсчета, а значит, не зависит от того, движется этот заряд или покоится.

В зависимости от концентрации свободных зарядов тела делятся на проводники, диэлектрики и полупроводники. Проводники — тела, в которых электрический заряд может перемещаться по всему его объему. Проводники делятся на две группы: 1) про­водники первого рода (металлы) — перенос в них зарядов (свободных электронов) не сопровождается химическими превращениями; 2) проводники второго рода (например, расплавленные соли, растворы кислот) — перенос в них зарядов (положительных и отрицательных ионов) ведет к химическим изменениям. Диэлектрики (например, стекло, пластмассы) — тела, в которых практически отсутствуют свободные заряды. Полупроводники (например, германий, кремний) занимают промежуточное положение между проводниками и диэлектриками. Указанное деление тел является весьма усло­вным, однако большое различие в них концентраций свободных зарядов обусловливает огромные качественные различия в их поведении и оправдывает поэтому деление тел на проводники, диэлектрики и полупроводники.

Единица электрического заряда (производная единица, так как определяется через единицу силы тока) — кулон (Кл) — электрический заряд, проходящий через попереч­ное сечение проводника при силе тока 1 А за время 1 с.

§ 78. Закон Кулона

Закон взаимодействия неподвижных точечных электрических зарядов установлен в 1785 г. Ш. Кулоном с помощью крутильных весов, подобных тем, которые (см. § 22) использовались Г. Кавендишем для определения гравитационной постоянной (ранее этот закон был открыт Г. Кавендишем, однако его работа оставалась неизвестной более 100 лет). Точечным называется заряд, сосредоточенный на теле, линейные раз­меры которого пренебрежимо малы по сравнению с расстоянием до других заряжен­ных тел, с которыми он взаимодействует. Понятие точечного заряда, как и материаль­ной точки, является физической абстракцией.

Закон Кулона:сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q ₁ и Q ₂ и обратно пропорциональна квадрату расстояния r между ними:

где k — коэффициент пропорциональности, зависящий от выбора системы единиц.

Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F <0) в случае разноименных зарядов и отталкиванию (F >0) в случае одноименных зарядов. Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид

(78.1)

где F ₁₂ — сила, действующая на заряд Q ₁ со стороны заряда Q ₂, r ₁₂ — радиус-вектор, соединяющий заряд Q ₂ с зарядом Q ₁, r = | r ₁₂| (рис. 117). На заряд Q ₂ со стороны заряда Q ₁ действует сила F ₂₁ = – F ₁₂.

В СИ коэффициент пропорциональности равен

Тогда закон Кулона запишется в окончательном виде:

(78.2)

Величина e₀ называется электрической постоянной; она относится к числу фундамен­тальных физических постоянных и равна

(78.3)

где фарад (Ф) — единица электрической емкости (см. § 93). Тогда

§ 79. Электростатическое поле. Напряженность электростатического поля

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем элект­рические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одной из форм существования материи, посредством которого осуществляются определенные взаимо­действия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы будем рассматривать элект­рические поля, которые создаются неподвижными электрическими зарядами и называ­ются электростатическими.

Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследу­емое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q ₀, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона (78.2), пропорци­ональна пробному заряду Q ₀. Поэтому отношение F/ Q ₀ не зависит от Q ₀ и характеризу­ет электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатичес­кого поля.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

(79.1)

Как следует из формул (79.1) и (78.1), напряженность поля точечного заряда в вакууме

(79.2)

Направление вектора Е совпадает с направлением силы, действующей на положитель­ный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положи­тельного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 118).

Из формулы (79.1) следует, что единица напряженности электростатического по­ля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — еди­ница потенциала электростатического поля (см. § 84).

Графически электростатическое поле изображают с помощью линий напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис. 119). Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности — радиальные прямые, выходящие из заряда, если он положителен (рис. 120, а), и входя­щие в него, если заряд отрицателен (рис. 120, б). Вследствие большой наглядности графический способ представления электростатического поля широко применяется в электротехнике.

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились про­водить их с определенной густотой (см. рис. 119): число линий напряженности, прони­зывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизыва­ющих элементарную площадку d S, нормаль n которой образует угол a с вектором Е, равно Е d S cos a = E_n d S, где Е_п —проекция вектора Е на нормаль n к площадке d S (рис. 121). Величина

называется потоком вектора напряженности через площадку d S. Здесь d S = d S n — век­тор, модуль которого равен d S, а направление совпадает с направлением нормали n к площадке. Выбор направления вектора n (а следовательно, и d S) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — 1 В×м.

Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверх­ность

(79.3)

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебра­ической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватыва­емой поверхностью.

В истории развития физики имела место борьба двух теорий: дальнодействия и близкодействия. В теории дальнодействия принимается, что электрические явления определяются мгновенным взаимодействием зарядов на любых расстояниях. Согласно теории близкодействия, все электрические явления определяются изменениями полей зарядов, причем эти изменения распространяются в пространстве от точки к точке с конечной скоростью. Применительно к электростатическим полям обе теории дают одинаковые результаты, хорошо согласующиеся с опытом. Переход же к явлениям, обусловленным движением электрических зарядов, приводит к несостоятельности те­ории дальнодействия, поэтому современной теорией взаимодействия заряженных ча­стиц является теория близкодействия.

§ 80. Принцип суперпозиции электростатических полей. Поле диполя

Рассмотрим метод определения модуля и направления вектора напряженности Е в каж­дой точке электростатического поля, создаваемого системой неподвижных зарядов Q ₁, Q ₂ ,..., Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил (см. § 6), т. е. результирующая сила F, дейст­вующая со стороны поля на пробный заряд Q ₀, равна векторной сумме сил F _i, приложенных к нему со стороны каждого из зарядов Q_i:

(80.1)

Согласно (79.1), F = Q ₀ E и F _i = Q ₀ Е _i, где Е —напряженность результирующего поля, а Е _i — напряженность поля, создаваемого зарядом Q_i. Подставляя последние выраже­ния в (80.1), получаем

(80.2)

Формула (80.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Принцип суперпозиции применим для расчета электростатического поля элект­рического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положи­тельному и равный расстоянию между ними, называется плечом диполя 1. Вектор

(80.3)

совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом (рис. 122).

Согласно принципу суперпозиции (80.2), напряженность Е поля диполя в произ­вольной точке

где Е₊ и Е_– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряжен­ность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолжении оси диполя в точке А (рис. 123). Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна

Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (79.2) для вакуума можно записать

Согласно определению диполя, l/ 2 <<r, поэтому

2. Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В (рис. 123). Точка В равноудалена от зарядов, поэтому

(80.4)

где r ' — расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е _B, получим

откуда

(80.5)

Подставив в выражение (80.5) значение (80.4), получим

Вектор Е_B имеет направление, противоположное вектору электрического момента диполя (вектор р направлен от отрицательного заряда к положительному).

§ 81. Теорема Гаусса для электростатического поля в вакууме

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом (1777—1855) теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверх­ность.

В соответствии с формулой (79.3) поток вектора напряженности сквозь сферичес­кую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре (рис. 124), равен

Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 125), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, таккак поток считается положитель­ным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/ e₀, т. е.

(81.1)

Знак потока совпадает со знаком заряда Q.

Рассмотрим общий случай произвольной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции (80.2) напряженность Е поля, создаваемого всеми зарядами, равна сумме напряженностей E _i полей, создаваемых каждым зарядом в отдельности: Поэтому

Согласно (81.1), каждый из интегралов, стоящий под знаком суммы, равен Q_i / e₀. Следовательно,

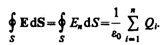(81.2)

Формула (81.2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e₀. Эта теорема выведена математически для векторного поля любой природы русским математиком М. В. Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом.

В общем случае электрические заряды могут быть «размазаны» с некоторой объемной плотностью r = d Q/ d V, различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V,

(81.3)

Используя формулу (81.3), теорему Гаусса (81.2) можно записать так:

§ 82. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме

1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +s(s = d Q/ d S — заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соsa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равенсумме потоков сквозь его основания (площади оснований равны и для основания Е_n совпадает с Е), т. е. равен 2 ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен s S. Согласно теореме Гаусса (81.2), 2 ES= s S/ e₀, откуда

(82.1)

Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + sи –s. Поле таких плоскостей найдемкак суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E =0. В области между плоскостями E = E ₊ + E _– (E ₊ и E _– определяются по формуле (82.1)), поэтому результирующая напряженность

Не нашли, что искали? Воспользуйтесь поиском: