
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение. Точка О называется полюсом, а луч l – полярной осью.
Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.
 |
М
r
r = 
j
l
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = rcosj; y = rsinj; x2 + y2 = r2
Пример. Уравнение кривой в полярной системе координат имеет вид:
 . Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
Воспользуемся связью декартовой прямоугольной и полярной системы координат: 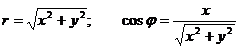 ;
;



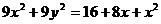


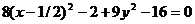
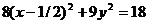

Получили каноническое уравнение эллипса. Из уравнения видно, что центр эллипса сдвинут вдоль оси Ох на 1/2 вправо, большая полуось a равна 3/2, меньшая полуось b равна  , половина расстояния между фокусами равно с =
, половина расстояния между фокусами равно с =  = 1/2. Эксцентриситет равен е = с/a = 1/3. Фокусы F1(0; 0) и F2(1; 0).
= 1/2. Эксцентриситет равен е = с/a = 1/3. Фокусы F1(0; 0) и F2(1; 0).

y

F1 F2
-1 0 ½ 1 2 x
- 
Пример. Уравнение кривой в полярной системе координат имеет вид:
 . Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
Подставим в заданное уравнение формулы, связывающие полярную и декартову прямоугольную системы координат.






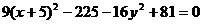


Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуось b равна 3, откуда получаем c2 = a2 + b2; c = 5; e = c/a = 5/4.
Фокусы F1(-10; 0), F2(0; 0).
Построим график этой гиперболы.
 |
y
F1 -9 -5 -1 0 F2 x
-3
Аналитическая геометрия в пространстве.
Уравнение линии в пространстве.
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0.
Это уравнение называется уравнением линии в пространстве.
Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
Тогда пару уравнений

назовем уравнением линии в пространстве.
Не нашли, что искали? Воспользуйтесь поиском: