Дві різні площини α і βпаралельні до площини γ. Доведіть, що площини α і β паралельні. Варіант 13

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. АВСDA₁B₁C₁D₁ – куб, пряма l проходить через вершину А₁ і середину ребра DC (мал. 1). Яку із зазначених прямих перетинає пряма l?

А) D₁D; Б) BС;

В) АA₁; Г) АD.

2. Які з тверджень є вірними:

1) пряма, що не лежить у площині трикутника, перетинає дві його сторони;

2) пряма не є паралельною площині на якій є прямі їй паралельні?

А) жодне; Б) перше; В) друге; Г) обидва.

3. Точка М рівновіддалена від вершин рівностороннього трикутника АВС (мал. 2), МО 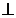(АВС). Знайдіть довжину проекції похилої МВ на площину АВС, якщо сторона трикутника см.

А) 8 см; Б) 4 см;

В) 15 см; Г) см.

4. Відрізок АВ не перетинає площину β, А₁В₁ — проекція відрізка АВ на площину β, АА₁ = 4 см, ВВ₁ = 10 см. Знайдіть відстань від середини відрізка АВ до площини β.

А) 14 см; Б) 7 см; В) 6 см; Г) 3 см.

5. Площа трапеції дорівнює 48 см², а кут між площиною її ортогональної проекції і площиною трапеції становить 60°. Знайдіть площу проекції даної трапеції.

А) 96 см²; Б) 18 см²; В) 24 см²; Г) 62 см^2..

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Складіть рівняння кола, що проходить через початок координат і має центр у точці А (4; 3).

7. Через вершину А паралелограма АВСD проведено площину α. Через точки В, С і D проведено паралельні прямі, які перетинають α в точках В₁, С₁, D₁ відповідно. Знайдіть DD₁, якщо ВВ₁ = 4 см, СС₁ = 12 см.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. Із середини М сторони АВ правильного трикутника АВС проведено до площини трикутника перпендикуляр МN; точка N сполучена з С. Доведіть, що СN АВ.

Варіант 14

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Які з наведених нижче тверджень правильні:

1) дві площини паралельні одній і тій самій прямій паралельні між собою;

2) пряма має спільну точку з однією з паралельних площин і не перетинає другу?

А) жодне; Б) перше; В) друге; Г) обидва.

2. Через точку М, що належить ребру ВD тетраедра АВСD, проведено площину, паралельну площині АВС. У скільки разів площа трикутника АВС більша за площу перерізу тетраедра АВСD даною площиною, якщо DМ: МВ = 1: 3?

А) у 3 рази; Б) у 4 рази; В) у 9 разів; Г) у 16 разів.

3. ABCDA₁B₁C₁D₁ паралелепіпед. Площинам яких граней паралельна пряма AD?

А) ABB₁A₁; Б) DD₁C₁С; В) A₁B₁C₁D₁; Г) AB₁C₁D.

4. Квадрат перегнули по діагоналі ВD так, що площини АВD і СВD стали перпендикулярними. Знайдіть відстань між точками А і С, якщо сторона квадрата дорівнює 1.

А) ; Б) 1; В) ; Г) 2.

5. Трикутник А₁В₁С₁ – проекція рівностороннього трикутника АВС. На стороні А₁В₁ відмічені точки K, L, N так, що А₁К = KL = LN = NB₁. Укажіть проекцію висоти трикутника АВС, опущеної з вершини С.

А) С₁К; Б) С₁L;

В) C₁N; Г) задача має неоднозначну відповідь.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Складіть рівняння кола що дотикається осі абсцис, якщо його центр знаходиться у точці А (1; 2).

7. Через вершину А паралелограма АВСD проведено площину α. Через точки В, С, D проведені паралельні прямі, які перетинають α в точках В₁, С₁ і D₁ відповідно. Знайдіть СС₁, якщо ВВ₁ = 3 см, DD₁ = 8 см.

IІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. Відрізок ВМ перпендикулярний до площини прямокутника АВСD. Доведіть, що пряма СD перпендикулярна площині МВС.

Варіант 15

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Точка О—центр правильного трикутника АВС, ОМ – перпендикуляр до площини АВС і ОМ = см, АО = 3 см. Знайдіть кут нахилу МА до площини трикутника АВС.

А) 60°; Б) 30º; В) 45°; Г) 90⁰.

2. Площина, перпендикулярна до катета АВ прямокутного трикутника АВС, перетинає його в точці М, а гіпотенузу АС — в точці N. Знайдіть МN, якщо АN = NС = 5, СВ = 6.

А) 3; Б) 4; В) 5; Г) 8.

3. Кінці відрізка АВ лежать у перпендикулярних площинах і β. Точка А віддалена від площини β на см, а точка В від площини – на см. Порівняйте значення параметрів і , якщо даний відрізок утворює кути 40º і 80º з площинами і β відповідно.

А) відповідь залежить від довжини відрізка АВ; Б) ;

В) ; Г) .

4. Яким може бути взаємне розташування двох прямих, одна з яких лежить в площині, а друга паралельна цій площині?

А) перпендикулярні; Б) паралельні;

В) паралельні або мимобіжні; Г) мимобіжні.

5. PАВСD – чотирикутна піраміда (мал. 1).Через точки С₁ і С₂, що належать ребру PС, паралельно до площини АВР проведено площини і відповідно. Площі перерізів піраміди PАВСD цими площинами дорівнюють S₁ і S₂ відповідно. Порівняйте величини S₁ і S₂, якщо це можливо.

А) S₁ > S₂; Б) S₁ < S₂;

В) S₁ = S₂; Г) порівняти неможливо.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. У колі проведено дві хорди, що перетинаються. Одна з них ділиться точкою перетину на відрізки 2 см і 6 см, а довжина другої — 7 см. Знайдіть відрізки другої хорди.

7. Побудуйте переріз прямої призми АВСA₁B₁C₁ площиною, що проходить через точку B₁ та точки М і К, що лежать на ребрах АС і АА₁ відповідно.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

Точка М знаходиться на відстані 3 см від кожної з вершин паралелограма, сторони якого відносяться як 2: 1. Знайдіть площу цього паралелограма, якщо відстань від точки М до площини паралелограма дорівнює 2 см. Варіант 16

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Якщо одна з двох паралельних прямих перпендикулярна до третьої прямої, то як розташовано другу пряму по відношенню до третьої?

А) паралельна; Б) перпендикулярна;

В) мимобіжна; Г) співпадають.

2. АВСDA₁B₁C₁D₁ − куб. Укажіть пряму перетину площин DВA₁ і DВC₁.

А) АВ; Б) D₁B₁;

В) DВ; Г) АС.

3. Паралелограм АВСD і трапеція АDFK (АD׀׀FK) не лежать в одній площині. Як розташовані пряма ВС і площина АКF?

А) пряма лежить в площині;

Б) пряма та площина перетинаються;

В) пряма та площина паралельні;

Г) визначити неможливо.

4. Кінці відрізка віддалені від площини на 2 см та 8 см. Проекція його на площину дорівнює 8 см. Якою є довжина самого відрізка?

А) 2 см; Б) 8 см; В) 10 см; Г) 5 см.

5. На площині взято точку А (мал. 3). Знайдіть відстань від даної точки до прямої перетину площин і β, якщо дана точка віддалена від площини β на 4 см, а кут між площинами дорівнює 45º.

А) 4 см; Б) см;

В) 8 см; Г) см.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. У трикутнику, площа якого дорівнює 48 см², проведено середню лінію. Знайдіть площу трикутника, який утворився.

7. Точка М – середина ребра ВС піраміди SABC. Побудуйте переріз піраміди площиною, що проходить через точку М і паралельна площині ASC та знайдіть площу перерізу, якщо SA = 24 см, SC = 10 см, АС = 26 см.

ІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. Ребро куба дорівнює а. Знайдіть найкоротшу відстаньміж діагоналлю куба і діагоналлю основи куба, які не мають спільних точок.

Варіант 17

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Через точку D проведено пряму DС, перпендикулярну до площини прямокутного рівнобедреного трикутника АВС ( С=90º). Відстані від точки D до точок А і В дорівнюють а см і b см відповідно. Порівняйте значення параметрів а і b, якщо це можливо.

А) a = b; Б) a < b; В) a > b; Г) порівняти неможливо.

2. АВСDA₁B₁C₁D₁ − прямокутний паралелепіпед. Укажіть пряму, по якій перетинаються площини АСВ₁ і АСD₁.

А) АВ; Б) А₁С₁;

В) DВ; Г) АС.

3. Відрізок АВ не перетинає площину β, А₁В₁ − проекція відрізка АВ на площину β, АА₁ = 2 см, ВВ₁ = 10 см. Знайдіть відстань від середини відрізка АВ до площини β.

А) 6 см; Б) 8 см; В) 4 см; Г) 12 см.

4. Кожна з площин α та β перпендикулярна до площини γ. Яким є взаємне розташування площин α та β?

А) перпендикулярні; Б) паралельні;

B) перетинаються; Г) визначити не можна.

5. Пряма а не лежить у площині . Скільки різних прямих, які є мимобіжними з прямою а, можна провести через точку, взяту в площині ?

А) жодної; Б) одна; В) безліч; Г) жодної або безліч.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Відношення катетів прямокутного трикутника дорівнює 12: 5. Гіпотенуза дорівнює 39 см. Знайдіть сторони трикутника.

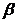7. Через точку С, що не належить двом паралельним площинам і , проведені два промені, один з яких перетинає площини і 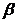в точках А₁ і В₁ відповідно, а другий – відповідно у точках А₂ і В₂. Відомо, що СА₁ = 4 см, В₁В₂ = 9 см, А₁А₂ = СВ₁. Знайдіть А₁А₂ і А₁В₁.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. До площини прямокутника із середини більшої сторони проведено перпендикуляр. Його кінець віддалений від однієї із діагоналей на 30 см. Знайдіть довжину перпендикуляра, якщо сторони прямокутника дорівнюють 45 см і 60 см.

Варіант 18

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Дано дві мимобіжні прямі а і b. Точки А і В лежать на прямій а, точки С і D на прямій b. Яке взаємне розміщення прямих АС і ВD?

А) паралельні; Б) мимобіжні;

В) перетинаються; Г) визначити неможливо.

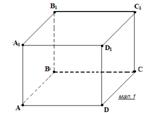2. АВСDA₁B₁C₁D₁ – куб, ребро якого дорівнює 2 (мал. 1). Знайдіть відстань від середини ребра C₁D₁ до площини АВС_.

А) 2; Б) ;

В) ; Г) 1.

3. На мал. 2 точка О — центр описаного навколо трикутника АВС кола, ОМ – перпендикуляр до площини АВС. Відстані від точки М до точок А і С дорівнюють а і с відповідно. Порівняйте величини а і с, якщо це можливо.

А) ; Б) ;

В) ; Г) порівняти неможливо.

4. Ребро РВ піраміди PАВС — перпендикуляр до площини основи АВС (мал. 3). Кут між площинами АВС і РАС дорівнює 30º. Знайдіть площу основи АВС піраміди, якщо площа грані РАС дорівнює см².

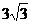А) см²; Б) см²;

В) 9 см²; Г) 12 см².

5. Дано трикутник АВС. Площина паралельна прямій АВ і перетинає сторону АС в точці К, а сторону ВС в точці М.Знайдіть довжину сторони АВ, якщо КС = 12 см, АС = 18 см, КМ = 36 см.

А) 4 см; Б) 54 см; В) 18 см; Г) 36 см.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Знайдіть площу круга, описаного навколо рівностороннього трикутника зі стороною 4 см.

7. Кінці відрізка розташовані по різні сторони від площини та віддалені від неї 5 см та 7 см. Знайдіть відстань від середини цього відрізка до цієї площини.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

Сторони прямокутника дорівнюють 9 см і 12 см. Із середини більшої сторони прямокутника проведено перпендикуляр до його площини довжиною 4,8 см. Знайдіть відстань від кінця цього перпендикуляра до діагоналей прямокутника. Варіант 19

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Паралельні площини і β перетинають сторони МN і NК кута МNК у точках А, L, В і R відповідно (мал. 1). Яке взаємне розміщення прямих АВ і LR?

А) перетинаються;

Б) мимобіжні;

В) паралельні;

Г) не можна визначити.

2. Точка А не належить площині квадрата. Скільки прямих, паралельних до осей симетрії квадрата можна провести через точку А?

А) 1; Б) 2; В) 3; Г) 4.

3. Точки А, В, С і D не лежать на одній площині. Яке взаємне розміщення прямих АВ і СD?

А) перетинаються; Б) мимобіжні;

В) паралельні; Г) лежать в одній площині.

4. Площини і β перетинаються по прямій .Точка А лежить в площині і знаходиться від прямої а на відстані в 2 рази більшій, ніж від площини β. Знайдіть кут між заданими площинами.

А) 90º; Б) 45º; В) 30º; Г) 60º.

5. До площини квадрата АВСD проведено перпендикуляр DМ довжиною 12 см. Сторона квадрата дорівнює 5 см. Знайдіть довжину похилої МА.

А) 15 см; Б) 13 см; В) 12 см; Г) см.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Знайдіть діаметр кола, описаного навколо правильного трикутника зі стороною, яка дорівнює см.

7. Гіпотенуза прямокутного трикутника дорівнює 12 см. Поза площиною трикутника дано точку, яка знаходиться на відстані 10 см від кожної його вершини. Знайдіть відстань від цієї точки до площини трикутника.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

Варіант 20

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

1. Які з наведених нижче тверджень правильні:

1) через три точки завжди можна провести тільки одну площину;

2) через три точки завжди можна провести безліч площин;

3) через три точки завжди можна провести одну або безліч площин?

А) жодне; Б) перше; В) друге; Г) третє.

2. Кут нахилу бічного ребра SВ піраміди SАВС до площини основи АВС – це кут…

А) SBC; Б) SBO;

В) SBA; Г) SKO.

3. Середини сторін просторового чотирикутника сполучені між собою відрізками. Яку фігуру утворюють ці відрізки?

А) паралелограм; Б) трапецію;

В) трикутник; Г) дельтоїд.

4. Площини квадратів АВСD і АВКL перпендикулярні, АВ = 2 см. Знайдіть відстань між точками К і D.

А) см; Б) 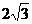см; В) 4см; Г) см.

5. Паралелограм АВСD і трапеція АDFK (АD ׀׀ FK) не лежать в одній площині. Як розташовані пряма КF і площина АВС?

А) пряма лежить в площині;

Б) пряма та площина перетинаються;

В) пряма та площина паралельні;

Г) визначити неможливо.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Складіть рівняння кола з центром на прямій у = 4, що дотикається до осі х у точці (−1; 0).

7. Знайдіть відстань від точки М до площини рівнобедреного трикутника АВС, знаючи, що АВ = ВС = 13 см, АС = 10 см, а точка М віддалена від кожної сторони трикутника на см.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.