Линейное преобразование

237. Задание {{ 331 }} ТЗ № 331

Отметьте правильный ответ

Пусть в базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= . Если а=5е₁+е₂-2е₃, то

£ а =е₁-е₂+2е₃

£ а =-9е₁

£ а =3е₁+2е₃

R а =-9е₁+16е₂

238. Задание {{ 332 }} ТЗ № 332

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= 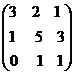. Если =2е₁+е₂-е₃, то

£ а =е₁+4е₂-е₃

£ а =2е₁-3е₂+е₃

£ а =е₂-2е₃

R а =7е₁+8е₂+4е₃

239. Задание {{ 333 }} ТЗ № 333

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= . Если а=е₁+е₂-2е₃, то

£ а =2е₂+е₃

£ а =2е₁+е₂+е₃

£ а =е₁-2е₃

R а =е₁+е₂-2е₃

240. Задание {{ 334 }} ТЗ № 334

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= . Если а=3е₁-е₂-е₃, то

R а =5е₁-е₂+7е₃

£ а =е₁-2е₂+3е₃

£ а =2е₁-2е₂+3е₃

£ а =5е₁-7е₂

241. Задание {{ 335 }} ТЗ № 335

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= . Если =е₁+2е₂+е₃, то

£ а =-е₁+е₂

£ а =3е₁-е₂

£ а =2е₁+5е₂+е₃

R а =е₁+13е₂+е₃

242. Задание {{ 336 }} ТЗ № 336

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= 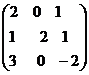. Если а=2е₁+5е₂-3е₃, то

£ а =2е₁+е₂+3е₃

£ а =е₁+е₂-2е₃

£ а =е₁-е₂+3е₃

R а =10е₂+13е₃

243. Задание {{ 337 }} ТЗ № 337

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= 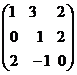. Если а=2е₁+е₂-5е₃, то

£ а =3е₁+е₂-е₃

£ а =2е₁+2е₂

£ а =е₁+2е₃

R а =-8е₁+12е₂+6е₃

244. Задание {{ 338 }} ТЗ № 338

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= . Если а=5е₁-3е₂+е₃, то

R а =4е₂-6е₃

£ а =2е₁+3е₂-е₃

£ а =2е₁+2е₂

£ а = е₂-3е₃

245. Задание {{ 339 }} ТЗ № 339

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= 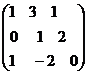. Если а=е₁-3е₂+2е₃, то

£ а =е₁ +е₃

£ а =3е₁+е₂-2е₃

£ а =е₁+2е₂

R а =3е₁-4е₂-5е₃

246. Задание {{ 340 }} ТЗ № 340

Отметьте правильный ответ

В базе е₁,е₂,е₃ 3-х мерного линейного пространства линейное преобразование задается матрицей А= . Если а=2₁-е₂+5е₃, то

£ а =3е₁-е₂

£ а =е₁+2е₂-е₃

£ а =2е₁+5е₂+е₃

R а =7е₁+4е₂-5е₃

Парабола

247. Задание {{ 261 }} ТЗ № 261

Отметьте правильный ответ

Геометрическое место точек плоскости, равноудаленных от данной точки и данной прямой называется

R параболой

£ эллипсом

£ гиперболой

248. Задание {{ 262 }} ТЗ № 262

Отметьте правильный ответ

Параболой называется геометрическое место точек плоскости, для которых расстояние до фокуса равно расстоянию до

R директрисы

£ асимптоты

£ Оси Ох

249. Задание {{ 263 }} ТЗ № 263

Отметьте правильный ответ

Каноническое уравнение параболы имеет вид

R у²=2рх

£ у=2рх

£ у=-2рх

250. Задание {{ 264 }} ТЗ № 264

Отметьте правильный ответ

Уравнение директрисы параболы имеет вид

R x+p/2=0

£ y+p/2=0

£ x=p/2+1

251. Задание {{ 265 }} ТЗ № 265

Отметьте правильный ответ

Что такое р в каноническом уравнении параболы у²=2рх

R параметр

£ эксцентриситет

£ Фокальный радиус

252. Задание {{ 266 }} ТЗ № 266

Отметьте правильный ответ

Если параметр р положительный, то точка параболы расположена

R В правой полуплоскости от оси Оу

£ В верхней полуплоскости от оси Ох

£ В левой полуплоскости от оси Оу

253. Задание {{ 267 }} ТЗ № 267

Отметьте правильный ответ

Эксцентриситет параболы равен

R 1

£ 0

£ >1

254. Задание {{ 268 }} ТЗ № 268

Отметьте правильный ответ

Отрезки, соединяющие точки параболы с фокусами, называется

R Фокальными радиусами

£ директрисами

£ асимптотами

255. Задание {{ 269 }} ТЗ № 269

Отметьте правильный ответ

Фокальный радиус r параболы вычисляется по формуле

R х+р/2

£ х+р

£ а- х

256. Задание {{ 270 }} ТЗ № 270

Отметьте правильный ответ

Что из нижеперечисленного верно

R Все перечисленное верно

£ х+р/2=0 - уравнение директрисы параболы

£ r=х+р/2 - фокальный радиус параболы

Не нашли, что искали? Воспользуйтесь поиском: