Основные теоретические положения. Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг неподвижной горизонтальной оси О

Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг неподвижной горизонтальной оси О, не проходящей через центр тяжести тела С и называемой осью качания маятника (рис. 2.1). Центр тяжести маятника совпадает с его центром масс. Точка пересечения оси качания маятника с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания, называется точкой подвеса маятника (т.О).

Если пренебречь силами трения в подвесе маятника, то момент относительно оси качания маятника создает только его сила тяжести . При отклонении маятника на угол a момент этой силы численно равен . Он стремится возвратить маятник в положение равновесия (a=0).

Поэтому в соответствии с основным законом динамики вращательного движения абсолютно твердого тела можно записать уравнение движения физического маятника для нашего случая

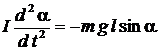, (2.1)

в котором a – угол отклонения маятника; – расстояние от центра масс маятника до оси подвеса; I – момент инерции маятника относительно той же оси; m – масса маятника; – угловое ускорение. При малых углах отклонения маятника , тогда уравнение (2.1) перепишется

. (2.2)

Следовательно, малые колебания физического маятника (a£10°) являются гармоническими с циклической частотой w, квадрат которой w² равен

, (2.3)

а сама частота w определяется формулой

. (2.4)

Период гармонических колебаний физического маятника равен

. (2.5)

В формуле (2.5) величина называется приведенной длиной физического маятника.

Точка О₁, находящаяся на расстоянии l ₀ от точки подвеса, называется центром качаний данного физического маятника (рис. 2.1).

Точка подвеса т.О и центр качаний т.О₁ обладают свойством обратимости: если перенести точку подвеса физического маятника в центр качаний, то прежняя точка подвеса окажется новым центром качаний, а период колебаний маятника не изменится. На этом свойстве основано устройство оборотного маятника.

Преобразуем соотношение (2.5), используя теорему Штейнера

, (2.6)

где I ₀ – момент инерции маятника относительно оси, проходящей через его центр тяжести (т.С) параллельно оси подвеса. Подставив равенство (2.6) в (2.5), находим

. (2.7)

Представляет интерес анализ зависимости периода Т колебаний физического маятника от величины l. В случае достаточно больших значений l соотношение (2.7) переходит в формулу для периода колебаний математического маятника

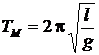. (2.8)

Рассмотрим возможность определения с помощью физического маятника ускорения свободного падения g. Входящую в формулу (2.7) величину I ₀, которую трудно найти из опыта, можно исключить, измеряя период колебаний при двух разных l ₁ и l ₂ (рис. 2.2). Преобразовав формулу (2.7), запишем ее для положений осей качаний т.О и т.О₁ (рис. 2.2) и получим систему уравнений

, (2.9)

, (2.10)

из которой находим

. (2.11)

Поскольку расстояния l ₁ и l ₂ взяты такими, что соответствующие им периоды равны T ₁= T ₂= T ₀, то из равенства (2.11) получаем

. (2.12)

При этом оси качаний расположены по разные стороны от центра тяжести т.С (рис. 2.2), тогда сумма (l ₁+ l ₂) есть расстояние между осями, которое равно приведенной длине физического маятника: l ₀=OO₁. Поэтому величину g можно найти из соотношения

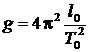. (2.13)

где T ₀ – период колебаний,одинаковый относительно двух осей (т.О и т.О₁).

Последняя формула аналогична по виду той, которую можно получить для ускорения свободного падения из формулы периода колебаний математического маятника (2.8). Таким образом, приведенной длиной физического маятника называют также длину некоторого математического маятника, который имеет тот же период колебаний, что и данный физический маятник.

Не нашли, что искали? Воспользуйтесь поиском: