Чтобы устранить неизбежные и большие случайные погрешности измерения, следует выбрать правильную методику измерений и обработки результатов.

Обсудим ошибки, возникающие при измерении времени пролета t. Уменьшение вклада случайных ошибок достигается многократным повторением каждого опыта в одинаковых условиях.

Рассмотрим теперь систематическую ошибку в измерении времени, которую обозначим D t. Неизвестное нам истинное время пролета t связано с измеренным временем пролета t_изм соотношением:

. (1.9)

Так как в формулу (1.8) входит истинное время t, то подставляя (1.9) в (1.8) получим:

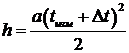. (1.10)

Таким образом, задача состоит в том, чтобы найти с помощью (1.10) ускорение а по измеренным значениям h и t_изм. Это лучше всего сделать, изображая h и t_изм на графике в координатах 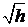и t_изм.

Извлекая корень квадратный из обеих частей равенства (1.10), найдем:

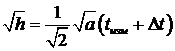. (1.11)

Как видно из последней формулы, 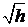и t_изм связаны между собой линейной зависимостью. График поэтому должен представлять собой прямую линию. Наличие ошибки D t приводит к тому, что эта прямая перестанет проходить через начало координат, но не нарушает прямолинейного характера графика и угла g наклона прямой к оси абсцисс, который зависит только от а:

. (1.12)

Поэтому определение тангенса угла наклона полученной прямой позволяет вычислить ускорение а вне зависимости от ошибки D t и найти саму эту ошибку. Ошибки измерений приводят к тому, что экспериментальные точки в координатах 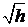и t_изм не лежат точно на прямой. Поэтому для построения графика используем метод наименьших квадратов (рис.1.4)

Описанный выше метод обработки наблюдений позволяет при данной величине перегрузка m₁ правильно измерить ускорение а. Но это найденное из эксперимента значение ускорения не может быть непосредственно использовано для определения ускорения свободного падения g, так как ускорение грузов зависит еще и от трения в оси блока. Ясно, что получить хорошие результаты эксперимента можно толь­ко при том условии, что вес перегрузка во много раз больше силы трения.

Сила трения определяется в основном весом груза m, а не весом перегрузка. Увеличивая массу перегрузка, мы улучшаем поэтому условия опыта. Следует также иметь в виду вес нити, влияющий на движение сложным образом, так как длина нити с каждой стороны блока зависит от времени. Это влияние, однако, также уменьшается с ростом m₁.

Величину массы перегрузка поэтому следует всячески увеличивать. Тем не менее, ее нельзя взять очень большой, так как при этом движение становится слишком быстрым, и точность измерения времени становится недостаточной. Лучше всего проводить измерения с не очень тяжелыми перегрузками и найти предел, к которому стремится вычисленное значение g при увеличении m₁ до больших значений, которые на опыте непосредственно применяться не могут.

Проще всего находить предел графически. Для этого следует построить график, в котором по оси абсцисс откладывается величина 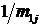, а по оси ординат – найденное при данном m_1j значение g_j. Проведенную через экспериментальные точки кривую нужно экстраполировать (продолжить) к большим значениям m₁, то есть к малым значениям 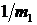, практически к 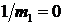. Найденное экстраполированное значение ускорения свободного падения и следует сравнивать с табличным (рис. 1.5).

Измерения проводятся в такой последовательности.

1. Перекинуть через блок нить с двумя грузами 3 и 4 и убедиться, что система находится в положении безразличного равновесия.

2. Установить кронштейн с фотодатчиком 6 в нижней части шкалы вертикальной стойки, а фотодатчик расположить таким образом, чтобы правый груз при движении вниз проходил в центре рабочего окна фотодатчика. За нижнее положение груза берется риска шкалы, соответствующая риске на корпусе фотодатчика, и являющаяся продолжением оптической оси фотодатчика, которую пересекает движущийся груз. Установить правый груз в крайнем верхнем положении, отметив его нижнюю кромку указателем 7.

3. Положить на правый груз один из перегрузков 5. Нажать на кнопку «ПУСК» блока. Происходит растормаживание электромагнита, правый груз начинает опускаться, и таймер электронного блока 8 начинает отсчет времени. При пересечении правым грузом оптической оси фотодатчика отсчет времени прекратится. Записать показания таймера, то есть время движения грузов.

4. Определить по шкале пройденный грузом путь h, как расстояние от нижней плоскости груза в верхнем положении до оптической оси фотодатчика.

5. Повторить измерения времени 4÷5 раз, записывая результаты t_i в таблицу.

6. Повторить измерения по п. 2÷5 с тем же перегрузком для 5 ÷ 6 других значений расстояния h_i.

7. Повторить измерения по п. 2÷6 для 4 ÷ 5 других значений массы перегрузка m_1j.

Обработка результатов эксперимента

1. Для каждого значения массы перегрузка m_1i полученные результаты изобразить графически в координатах 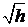и t_изм.

2. По формулам (П2.4) и (П2.5) метода наименьших квадратов из Приложения 2 найти тангенс угла наклона прямой к оси абсцисс А и величину В, отсекаемую этой прямой на оси ординат для каждого исследуемого значения массы перегрузки, при этом , .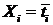

3. Зная тангенсы углов наклона, определить значение ускорения по формуле (1.12) для каждой исследуемой массы перегрузка.

4. Определить ускорение свободного падения по формуле (1.7) для каждой исследуемой массы перегрузка.

5. Для каждого значения массы перегрузка m_1j полученные результаты расчета g_j изобразить графически в координатах .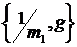

6. С помощью метода наименьших квадратов найти экстраполированное значение для случая 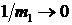по формуле (П2.5) Приложения 2, где , .

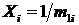7. Сравнить полученный результат с ускорением свободного падения для широты Саратова j, которое рассчитать по формуле:

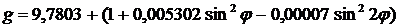. (1.13)

Расчет погрешностей

1. Погрешность измерения ускорения свободного падения рассчитать по формулам (П2.6) – (П2.8) Приложения 2, где , .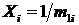

2. Результат представить в виде .

Лабораторная работа № 2

ОПРЕДЕЛЕНИЕ момента инерции твердого тела

на основе законов равноускоренного движения

Цель работы: изучение законов динамики вращательного движения, определение момента инерции и момента сил трения маятника Обербека

Основные теоретические сведения

Вращательным движением тела называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями с центрами на одной прямой, называемой осью вращения.

Для характеристики быстроты и направления вращения твердого тела вокруг оси служит угловая скорость. Угловой скоростьюназывается вектор 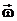, численно равный производной от угла поворота по времени и направленный вдоль неподвижной оси вращения так, чтобы из его конца вращение тела было видно против часовой стрелки.

Угловым ускорениемназывается вектор 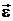, модуль которого равен производной от его угловой скорости по времени 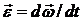. Если тело вращается вокруг неподвижной оси, то вектор 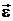направлен вдоль этой оси: в ту же сторону, что 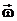, при ускоренном вращении 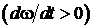и в противоположную сторону при замедленном вращении .

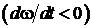Моментом силы относительно неподвижной точки О называется векторная величина 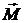, равная векторному произведению радиуса-вектора 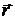, проведенного из точки О в точку А приложения силы (рис. 2.1), на вектор силы :

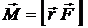. (2.1)

Модуль момента силы определяется выражением M = F r sina = F l, где a – угол между векторам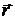и и . Величина l = r sina, равная длине перпендикуляра ОВ, опущенного из точки О на линию действия силы, называется плечом силы относительно точки О. Когда сила приложена к одной из точек твердого тела, то вектор 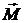характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтому момент силы называют также вращательным моментом.

Главным или результирующим моментом системы сил относительно точки О называется вектор 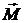, равный геометрической сумме моментов всех n сил системы:

, (2.2)

где – вектор, проведенный из точки О в точку приложения силы .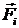

Из третьего закона Ньютона следует, что моменты относительно точки О внутренних сил взаимодействия материальных точек системы попарно компенсируются. Следовательно, при вычислении главного момента сил надо учитывать только внешние силы, действующие на рассматриваемую механическую систему.

Моментом силы относительно неподвижной оси a называется скалярная величина M _a, равная проекции на эту ось вектора момента силы 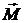относительно произвольной точки О оси a. Значение момента M _a не зависит от выбора положения точки О на оси a.

При вращательном движении твердого тела вокруг неподвижной оси мерой его инертности является величина, называемая моментом инерции I, подобно тому, как масса тела является мерой его инертности в поступательном движении.

Моментом инерции I материальной точки относительно неподвижной оси вращения называется величина, равная произведению ее массы на квадрат расстояния до оси вращения: I = m r ².

Абсолютно твердое тело эквивалентно системе большого числа n материальных точек. Моментом инерциимеханической системы (в данном случае твёрдого тела) называется физическая величина I, равная сумме произведений масс всех материальных точек на квадрат их расстояний до оси вращения.

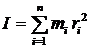. (2.3)

Момент инерции абсолютно твердого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера момент инерции I относительно произвольной оси равен сумме момента инерции этого тела I_C относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями

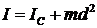. (2.4)

Основной закон динамики вращательного движения твердого тела определяет взаимную связь между моментом силы 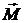, моментом инерции I и угловым ускорением 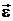. В векторной форме он записывается следующим образом

. (2.5)

Экспериментальная установка и методика измерений

В работе определяется момент инерции маятника Обербека, схема которого представлена на рис.2.2. Вращение маятника происходит под действием момента 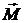силы натяжения нити и противоположно направлению момента сил трения 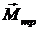. Тогда уравнение движения маятника (2.5) в проекции на ось вращения имеет вид

M = I e + M_тр. (2.6)

Из равенства (2.6) ви 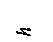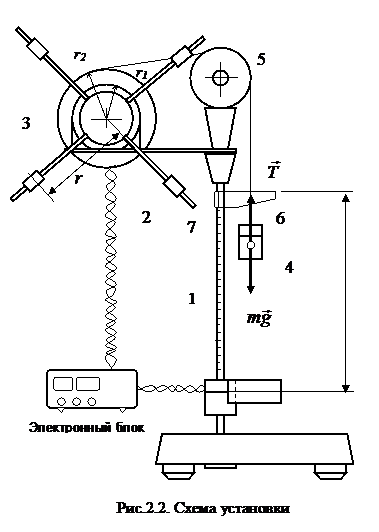дно, что если сила трения постоянна (не зависит от скорости), то зависимость величины M от e является линейной функ­ци­ей вида y = Ax + B. При этом I играет роль углового коэффициента А. Таким образом, экспериментальное исследование взаимосвязи между моментом силы натяжения M и угловым ускорением e позволяет найти момент инерции маятника I.

Движение гири 4 происходит под действием силы тяжести mg (где m – масса гири, g – ускорение свободного падения) и силы натяжения нити T. Согласно второму закону Ньютона, уравнение движения гири имеет вид

m a = m g – T, (2.7)

Здесь a – ускорение движения гири, которое можно найти, зная время t ее опускания и пройденный путь h. Используя известное уравнение равноускоренного движения, имеем

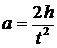. (2.8)

Из равенств (2.7) и (2.8) получаем выражение для определения момента силы натяжения

, (2.9)

где r_i – радиус шкива, который равен или r ₁ или r ₂ (рис.2.2).

Учитывая соотношение a = e r_i, связывающее угловое и линейное ускорения для точек на окружности шки­ва, из формулы (2.8) находим

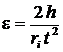. (2.10)

Итак, формулы (2.9) и (2.10) позволяют найти по экспериментальным данным момент силы натяжения M и угловое ускорение e. Тогда, проведя опыты с гирями различной массы m, можно исследовать зависимость M от e и построить соответствующий график.

Таким образом, определение момента инерции колеса сводится к определению углового коэффициента найденной из опыта функции M (e) (2.6).

Исследуемое тело 1 состоит из четырех стержней, укрепленных во втулке. На стержнях закрепляются грузы 2, перемещая которые, можно изменять момент инерции тела. На одной оси с телом находятся два шкива 3 радиусами r ₁ = 2 см и r ₂ = 3,5 см. Ось закреплена в подшипниках так, что вся система может вращаться вокруг горизонтальной оси. Гиря 4, приводящая тело во вращение, прикреплена к концу нити, которая перекинута через блок 5 и наматывается на один из шкивов 3. На основную гирю массой m ₀ могут надеваться от одного до четырех дополнительных грузов 6.

Эксперимент осуществляется в такой последовательности.

1. Подготавливая установку к измерениям, необходимо установить стойку так, чтобы гиря при опускании не задевала фотоэлементы. Установить грузы по осям крестовины на концах стержней. К одному из шкивов 3 прикрепить нить, к другому концу нити повесить гирю 4 и перекинуть нить через верхний шкив 5. Установить при помощи разновесов 6 массу гири, большую, чем минимальная масса, при которой маятник начинает вращаться.

2. Вращая маятник, установить груз в крайнее верхнее положение таким образом, чтобы нижняя плоскость гири совпала с одной из рисок шкалы вертикальной стойки, для чего использовать флажок 7. Записать это значение, учитывая, что максимальное перемещение груза не менее 25 см.

3. Зафиксировать груз в этом положении. Для этого нажать на кнопку «СЕТЬ» блока, при этом должен сработать фрикцион электромагнита.

4. Установить кронштейн с фотодатчиком в нижней части шкалы вертикальной стойки и расположить фотодатчик 7 таким образом, чтобы гиря с дополнительными грузами при движении вниз проходила по центру рабочего окна фотодатчика. За нижнее положение гири берется отметка шкалы, соответствующая риске на корпусе фотодатчика и являющаяся продолжением оптической оси фотодатчика, которую пересекает движущаяся гиря.

5. Нажать на кнопку «ПУСК» блока. Происходит растормаживание электромагнита, гиря начинает опускаться, и таймер блока начинает отсчет времени. При пересечении оптической оси фотодатчика отсчет времени прекратится. Показание таймера определяет время движения гири t.

Определить по шкале пройденный грузом путь h, это расстояние от нижней плоскости гири в верхнем положении до оптической оси фотодатчика. Записав значения h, r, m, t, нажать клавишу «СБРОС». Для повышения точности измерений повторить опыт до 3 ¸ 5 раз и найти среднее значение времени.

6. Повторить измерение п. 5 при тех же значениях h и r, увеличивая массу гири с помощью дополнительных грузов. Провести измерения для 3 ¸ 4 значений m. Результаты измерений записать в таблицу.

7. Выполнить задания п. 5 и п. 6 при других положениях грузов 2, изменяя r в пределах от 6 см до 14 см. Результаты измерений для каждого r записать в таблицу.

Обработка результатов эксперимента

1. Для каждого выбранного значения положения грузов на стержнях r рассчитать по формулам (2.9) и (2.10) величины M и e при различных m. Результаты вычислений записать в таблицу.

2. В каждом случае построить график функции M (e). Аппроксимировать экспериментальные результаты линейной зависимостью M=A e+ B по методу наименьших квадратов Приложения 2 и найти величины A и B по формулам (2п.4) и (2п.5), в которых X_i = e _i, Y_i = M_i.

3. Для каждого выбранного положения грузов определить момент инерции маятника Обербека I = A и момент сил трения M_TP = B.

4. Построить график зависимости момента инерции от положения грузов на стержнях I (r).

Расчет погрешностей

1. Вычислить погрешность определения момента инерции D I = D A по формулам (П2.6) и (П2.8) Приложения 2, в которых X_i = e _i, Y_i = M_i.

2. Результат представить в виде .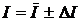

3. Вычислить погрешность определения момента сил трения D M_TP = D B по формулам (П2.7) и (П2.8) Приложения 2, в которых X_i = e _i, Y_i = M_i.

4. Результат представить в виде .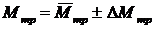

Не нашли, что искали? Воспользуйтесь поиском: