Позначення та приклади

А.В. Тушев

„ЕЛЕМЕНТИ ЗАГАЛЬНОЇ ТОПОЛОГІЇ”

(Опорний конспект лекцій)

Дніпропетровськ

РВВ ДНУ

ЗМІСТ

ЗМІСТ

1. Метричні простори.

2. Відкриті множини метричних просторів та їх властивості.

3. Топологія. Топологічні простори. Приклади.

4. Замкнені підмножини топологічного простору.

5. Внутрішні точки. Внутрішність підмножини топологічного простору.

6. Точки дотику. Замикання підмножин топологічного простору.

7. Ізольовані, граничні, межові точки.

8. База топологічного простору. Введення топології за допомогою бази.

9. Неперервне відображення топологічних просторів. Гомеоморфізми.

10. Компактні топологічні простори.

Список використаної літератури.

§1. Метричні простори.

Позначення та приклади

Нехай М – множина. Метрикою, заданою на М, називається закон (правило), який кожній упорядкованій парі елементів із М ( М) ставить у відповідність деяке дійсне, невід’ємне число , причому так, що виконуються наступні аксіоми:

М1. Аксіома тотожності:

М2. Аксіома симетричності:

М3. Аксіома трикутника:

Таким чином, метрика на М – це відображення , яке задовольняє аксіомам М1 – М3.

Якщо на М задана метрика , то пару називають метричним простором з метрикою .

Елементи простору М називають його точками, а величину - відстанню між точками а і в.

Зазначимо, що поняття метрики узагальнює поняття відстані з Евклідової геометрії, оскільки ця відстань задовольняє означенню метрики.

Приклади:

1. На множині R введемо метрику за правилом: =| a - в |.

Аксіоми М1, М2 – очевидні. А оскільки

,

то отримали аксіому М3. Таку метрику називають природною.

1. Дискретна метрика.

Нехай М – довільна множина, введемо на М метрику наступним чином:

Аксіоми М1, М2 – очевидні з означення цієї метрики. 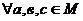розглянемо усі можливі значення метрик із співвідношення:

(*)

Якщо =0, то співвідношення (*) виконується незалежно від значень метрик у його правій частині. Якщо ж =1, то

Таким чином, - метрика на М, яку називають дискретною метрикою на М.

1. Нехай Е – п -вимірний Евклідовий простір, тобто Е – п -вимірний векторний простір над полем R, на якому введений скалярний добуток (<a,в>). За допомогою скалярного добутку вводиться довжина вектору евклідового простору

4. - множина усіх можливих рядків довжини п з дійсними коефіцієнтами . Відомо, що - векторний простір над полем R.

Якщо операцію додавання і зовнішнього множення ввести по-координатно, крім того є векторним простором і скалярний добуток ввести за формулою:

Тоді згідно приклада 3: - метричний простір, на якому метрика задається за формулою:

(1)

Метрику на , введену за формулою (1), називають Евклідовою.

5. Окрім Евклідової метрики, що була введена на за формулою (1), на цій множині можна ввести й інші метрики:

Перевіримо аксіоми метрики для :

М1:

М2:

М3:

Крім того, на можна ввести ще метрику за формулою:

М1:

М2:

М3:

Таким чином, на одній і тій же множині М, у загальному випадку, можна ввести багато метрик, тому позначення метрик у позначенні метричного простору відіграє суттєву роль: різні метричні простори. Але якщо заздалегідь відомо, про яку метрику йде мова, то метричний простір можна позначити лише символом, що позначає множину, на якій задана метрика.

6. Нехай - множина неперервних на відрізку функцій.

На цій множині можна ввести метрики, наприклад за формулою

.

Але на можна ввести й інші метрики, наприклад за такою формулою:

§2. Відкриті множини метричних просторів та їх властивості

Нехай - метричний простір, - елемент простору, .

Множина називається відкритою кулею з центром у точці і радіусом .

Множина називається замкненою кулею з центром у точці і радіусом .

Множина називається сферою з центром і радіусом .

Множину називають -околом точки .

В метричному просторі можна ввести означення відстані між його підмножинами,а саме, якщо , то .

Означення відстані між підмножинами дозволяє ввести означення -околу підмножини А метричного простору. А саме, якщо міститься в М, то

Нехай М - метричний простір, U – підпростір простору М, називають відкритою множиною, якщо або U – пуста множина, або будь-яка точка з U входить в U разом з деяким своїм -околом. Тобто

Твердження 1: Нехай М – метричний простір, , тоді:

1. Відкрита куля 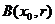- відкрита множина.
2. - відкрита множина.

Теорема 2 (властивості відкритих множин метричного простору):

Нехай М – метричний простір, тоді сукупність усіх відкритих множин простору М задовольняє наступним властивостям:

1. Пуста підмножина та вся множина М є відкритими.
2. Об’єднання будь-якої кількості відкритих підмножин простору М є множиною відкритою.
3. Перетин будь-якої скінченної сукупності відкритих підмножин з М – відкрита множина в М.

Зауваження: Перетин нескінченної сукупності відкритих підмножин метричного простору може бути відкритим.

Розглянемо відкриті підмножини:

не є відкритою підмножиною, оскільки ніякий окіл числа 1 не попадає в множину (0,1].

Твердження 2: Підмножина U множини М є відкритою тоді і тільки тоді, коли U є об’єднанням деякої сукупності відкритих куль з М.

§3. Топологія. Топологічні простори. Приклади

Нехай Т – деяка множина, тоді булеан - сукупність усіх підмножин.

Деяка сукупність підмножин множини називається топологією на множині Т, якщо задовольняє наступним аксіомам (аксіомам топології)

Т1: пуста множина, сама множина Т містяться в .

Т2:

Об’єднання будь-якої сукупності підмножин з також належить до .

Т3:

Перетин скінченної сукупності підмножин з належить до .

Якщо на множині Т задана деяка топологія , то пару (Т, ) називають топологічним простором. При цьому елементи множини Т називаються точками цього простору. А підмножини з називаються відкритими підмножинами з цього простору.

Якщо заздалегідь невідомо, про яку топологію на Т йде мова, то для позначення топологічного простору можна використовувати лише позначення множини Т.

Приклад 1: (М, ) – деякий метричний простір.

Нехай - сукупність всіх відкритих підмножин цього простору. За теоремою задовольняє всім аксіомам топології, тоді (М, ) є топологічним простором. Цю топологію називають топологією на М, індукованою метрикою , і позначається .

Таким чином, поняття топологічного простору є деяким узагальненням метричного простору.

Нехай (Т, ) – деякий топологічний простір. Якщо на множині Т можна задати метрику , так що (Т, )=(Т, ), то кажуть, що топологія є метризованою.

Зазначимо, що далеко не всі топології є метризованими.

Приклад 2: Нехай Т – множина. = , тоді - топологія на Т, яку називають дискретною. Зазначимо, що дискретна топологія індукована дискретною метрикою. У цій топології усі підмножини з Т є відкритими. І зокрема, точки дискретного простору є відкритими підмножинами.

Приклад 3: Нехай Т – множина. , задовольняє всім аксіомам топології. Цю топологію називають тривіальною топологією на Т.

Приклад 4: Нехай Т – нескінченна множина, покладемо:

є топологією на Т, яку називають топологією скінченних доповнень (топологією Заріського).

Приклад 5: Нехай (Т, ) – топологічний простір і нехай

Покажемо, що є топологією на множині А.

Таким чином, - топологія на підмножині А, яку називають топологією, індукованою на А топологією називають підгрупою простору .

Таким чином, всяку підмножину простору Т можна розглядати як його підпростір з індукованою топологією.

Якщо , то - слабкіша, - сильніша. Найслабкіша – тривіальна , найсильніша – дискретна

§4. Замкнені підмножини топологічного простору

- топологічний простір, називається замкненою, якщо - відкрита множина.

Приклад 1:

- метричний простір, як було доведено раніше 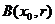і - відкриті множини, тому множини та є множинами замкненими

.

Приклад 2:

У дискретній топології замкненими будуть усі підмножини, оскільки в ній всі підмножини відкриті.

Приклад 3:

У топології скінченних доповнень, задані на нескінченній множині Т (топології Заріського) замкненими будуть та усі скінченні підмножини з Т.

Теорема 1 (властивості замкнених підмножин):

Нехай - топологічний простір. -сукупність усіх замкнених підмножин цього простору, тоді має наступні властивості:

1.

2. Перетин будь-якої сукупності замкнених підмножин з Т є підмножина замкнена.

3. Об’єднання будь-якої скінченної сукупності замкнених підмножин з Т є підмножина замкнена.

підмножиною, оскільки її доповнення не є відкритою.

Теорема 2 (про введення топології за допомогою системи замкнених підмножин):

Нехай Т – деяка множина, , що задовольняє вимогам (1)-(3) попередньої теореми, тоді на множині Т існує топологія , для якої є системою замкнених підмножин.

§5. Внутрішні точки.

Внутрішність підмножини топологічного

Простору

Т – топологічний простір, Довільна відкрита підмножина з Т, що містить А називається (відкритим) околом множини А.

Нехай Т – топологічний простір, Точка називається внутрішньою точкою А, якщо .

Сукупність усіх внутрішніх точок множини А називають внутрішністю цієї множини (Int A)

Твердження 1: Нехай Т – топологічний простір, Тоді Int A співпадає з об’єднанням усіх відкритих підмножин, що містяться в А.

Наслідок 1: IntA є найбільшою відкритою підмножиною, що міститься в А.

Наслідок 2: Множина А є відкритою тоді і тільки тоді, коли А=IntA.

Приклад 1: Розглянемо простір R, тоді Int [a, b]=(a, b)

Приклад 2: Розглянемо R, . Оскільки будь-який відкритий окіл як раціональні, так і ірраціональні числа, то

§6. Точки дотику. Замикання підмножин топологічного простору

Нехай Т – топологічний простір, називається точкою дотику до підмножини А, якщо .

Сукупність усіх точок дотику А називається замиканням підмножини А. ([А])

Теорема (властивості операції замикання):

Нехай Т – топологічний простір, тоді операція замикання в Т має такі властивості:

1.

2.

3.

4.

Наслідок. Нехай Т – топологічний простір, - замкнена тоді і тільки тоді, коли

.

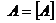Твердження: Нехай Т – топологічний простір, Тоді 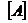- перетин усіх замкнених підмножин з Т, що містять А.

§7. Ізольовані, граничні, межові точки

Нехай Т – топологічний простір, Тоді

Точка К, яка належить множині А, називається ізольованою точкою множини А, якщо

Множина усіх ізольованих точок з А позначається IsA.

Точка х, яка належить множині Т, називається граничною, якщо

. Множина усіх граничних точок А позначається і називається похідною множини А.

Точка х, яка належить множині Т, називається межовою точкою множини А, якщо . Сукупність межових точок – це межа А (FrA).

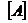Твердження 1: Нехай Тоді розпадається на три множини, що не перетинаються:

1. IsA.
2. - граничні точки А, що належать А.
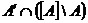3. - граничні точки А, що не належать А.

Наслідок 1: Підмножина А множини Т є замкненою тоді і тільки тоді, коли вона містить усі свої граничні точки.

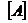Твердження 2: Нехай Тоді розпадається в об’єднання трьох підмножин, що не перетинаються:

Наслідок 2: є замкненою тоді і тільки тоді, коли вона містить усі свої межові точки.

Наслідок 3: Тоді:

1.

2.

3.

Приклади: 1.

2.

§8. База топологічного простору. Введення топології за допомогою бази

Нехай - топологічний простір, - його топологія. називається базою топології , якщо будь-яка підмножина з є об’єднанням деякої сукупності підмножин з (при цьому вважається, що є об’єднанням пустої сукупності підмножин з ).

Твердження 1 (критерій бази): - топологічний простір. є базою топології тоді і тільки тоді, коли

Доведення: Припустимо, що - база топології . Виберемо довільну точку і деякий її окіл . Оскільки є відкритою множиною, то він є об’єднанням деякої сукупності підмножин . Оскільки , то з означення об’єднання випливає, що .

Припустимо тепер, що задовольняє умові критерію, і покажемо, що тоді - база топології , тобто будь-яка відкрита підмножина є об’єднанням деякої сукупності підмножин з .

Дійсно, оскільки - відкрита, то . Тоді за умовою критерію:

. Все доведено.

Приклади: 1. З розділу “Відкриті підмножини метричного простору ” випливає, що утворює базу індукованої топології . Оскільки будь-яка відкрита підмножина з М є об’єднанням деякою сукупності відкритих куль. Але ця топологія має і меншу базу: .

1. В природній топології числової прямої R базу утворюють усі обмежені відкриті інтервали . Відзначимо, що хоча ця топологія на R має потужність контінум, але вона має зліченну базу , що випливає з критерію бази.

Твердження 2 (необхідна умова бази): Нехай - топологічний простір. Якщо є базою топології , то задовольняє наступним умовам:

1.

2.

Теорема(про введення топології за допомогою бази): Нехай Т – деяка множина і . Припустимо, що задовольняє умовам 1) і 2) попереднього твердження, тоді існує єдина топологія на Т, для якої є базою.

§9. Неперервне відображення топологічних просторів. Гомеоморфізми

Нехай X, Y - топологічні простори. Відображення називається неперервним в точці , якщо .

Якщо відображення - неперервне в , то воно називається неперервним відображенням топологічних просторів.

Нехай 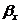- деяка база простору Х, - деяка база простору Y. Означення неперервності відображення можна ввести, використовуючи тільки елементи баз цих просторів, а саме:

Твердження 1: Нехай X, Y - топологічні простори, 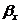, - їх бази. Відображення буде неперервним в тоді і тільки тоді, коли

Розглянемо тепер неперервні відображення метричних просторів.

Оскільки сукупність усіх -околів метричного простору утворює базу його топології, то можна ввести наступні означення неперервності відображень метричних просторів.

Нехай X, Y - метричні простори, , . Відображення називається неперервним в точці х, якщо:

.

Оскільки і є елементами бази просторів X, Y, то згідно твердження 1, це означає еквівалентне означенню неперервності відображення топологічних просторів. В окремому випадку числових функцій (функцій, заданих на просторі R) означення неперервності має наступний вигляд:

Функція f неперервна в точці , якщо:

Твердження 2 (критерій неперервності відображень топологічних просторів):

Нехай X, Y - топологічні простори, неперервне тоді і тільки тоді, коли:

1. Прообраз будь-якої відкритої множини з Y є відкритою множиною в X.
2. Прообраз будь-якої замкненої множини з Y є замкненою множиною в X.

Твердження 3: Композиція (суперпозиція) неперервних відображень топологічних просторів є неперервним відображенням, тобто, якщо X, Y, Z – топологічні простори, і - їх неперервні відображення, то є неперервним відображенням топологічних просторів.

Нехай X, Y – топологічні простори. Відображення називається гомеоморфізмом, якщо f – бієктивне, неперервне і зворотне до нього відображення.

також є неперервним.

Якщо між просторами X та Y існує гомеоморфізм, то такі простори називаються гомеоморфними і позначаються так: .

Нехай X, Y – топологічні простори. Відображення називається:

1) відкритим, якщо образ будь-якої відкритої множини є відкритою множиною в Y.

2) замкненим, якщо образ будь-якої замкненої множини з X є замкненою множиною в Y.

Твердження 4: Нехай X, Y – топологічні простори, бієктивне неперервне відображення є гомеоморфізмом тоді і тільки тоді, коли воно є відкритим (замкненим).

Наслідок: Якщо між топологічними просторами X, Y існує гомеоморфізм , то для довільної множини виконуються співвідношення:

1.

2.

3.

Якщо між топологічними просторами існує гомеоморфізм, то вони мають однакові топологічні властивості. У загальній топології гомеоморфні простори вважаються однаковими.

Твердження 5: Гомеоморфність є співвідношенням еквівалентності на класі усіх топологічних просторів, тобто:

1.

2.

3.

Сукупність усіх топологічних просторів розпадається на класи гомеоморфних просторів і вони не перетинаються. Ці класи називаються топологічними типами. Гомеоморфні простори мають однакові топологічні типи.

§10. Компактні топологічні простори

Нехай X – топологічний простір. Деяка сукупність підмножин називається покриттям простору X, якщо .

Якщо , то система підмножин називається покриттям множини А, якщо .

Якщо всі - відкриті, то покриття називається відкритим. Підпокриттям називається деяка сукупність множин з покриття. Топологічний простір X називається компактним, якщо з будь-якого відкритого його покриття можна виділити скінченне підпокриття.

Приклади:

1. Числова пряма не є компактним простором, оскільки з його покриття інтервали вигляду неможливо виділити скінченне підпокриття.
2. Скінченний відкритий інтервал (0, 2) не є компактним простором, оскільки з його покриття інтервали вигляду неможливо виділити скінченне підпокриття.
3. Замкнений інтервал є компактним простором, що доводиться в лемі Гейне-Бореля.

Нехай Х – деяка множина, - деяка система підмножин з множини Х. називається центрованою, коли кожна скінченна підсистема підмножин з має непустий перетин.

Твердження 1 (критерій компактності простору):

Топологічний простір Х є компактним тоді і тільки тоді, коли кожна центрована система його замкнених підмножин має непустий перетин.

Підмножина А топологічного простору Х називається компактною, якщо підпростір є компактним.

Твердження 2: Підмножина А топологічного простору Х є компактною тоді і тільки тоді, коли з кожного покриття множини А відкритими в Х підмножинами можна виділити скінченне підпокриття.

Твердження 3: Всяка замкнена підмножина А топологічного простору Х є компактною множиною цього простору.

Список використаної літератури.

1. Александрян Г.А., Мирзаханян Э.А. Общая топология. – М.: Высш. шк. 1979. – 396 с.

2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1989. – 624 с.

3. Мищенко А.С., Фоменко А.Т. Курс дифференциальной геометрии и топологии. – М.: МГУ. 1980. – 439с.

Не нашли, что искали? Воспользуйтесь поиском: