
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Равносторонний треугольник.
 S =
S = 
10. Правильные многоугольники (все стороны равны).
R =  ; a – сторона, n – количество сторон, r =
; a – сторона, n – количество сторон, r =  ; a – сторона, n – количество сторон
; a – сторона, n – количество сторон
| n | R | r |
| n = 3 | 
| 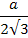
|
| n = 4 | 
| 
|
| n = 6 | a | 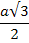
|
Площадь фигур.
Треугольник
S  =
=  a
a  h S
h S  =
= 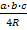 S
S  =
=  P
P  r
r
S  =
=  a
a  b
b  a S
a S  =
=  ;
;
p =  (a + b + c)
(a + b + c)
Свойства площадей треугольника:
 a) Если треугольники имеют общую высоту, то их площади относятся, как основания, к которым проведена эта высота;
a) Если треугольники имеют общую высоту, то их площади относятся, как основания, к которым проведена эта высота;
 =
= 
б) площади 2-х треугольников имеющие общую сторону, относятся как высоты, проведенные к этой стороне;
 =
= 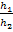

в) площади треугольника имеющие общий угол, относятся как произведения сторон заключающих этот угол.
 =
= 

2) четырехугольники
а) параллелограмм S = a  h, S = a
h, S = a  b
b  sina, S =
sina, S =  d1
d1  d2
d2  sinb
sinb

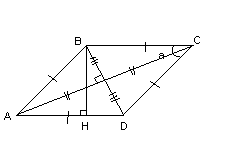
Свойство диагоналей:
d12 + d22 = 2a2 + 2b2 (сумма квадратов диагоналей равна сумме квадратов всех сторон).
Б) ромб
S = a  h, S = a2
h, S = a2  sina, S =
sina, S =  d1
d1  d2
d2
в) прямоугольник
 d1=d2, S = a
d1=d2, S = a  b, S =
b, S =  d2
d2  sinb, R =
sinb, R =  d
d
Г) квадрат
 d = a
d = a  2, S =
2, S =  d2 S = a2
d2 S = a2
Д) трапеция

QP – средняя линия (средняя линия параллельна основаниям и равна их полусумме).
S = MN  h, S =
h, S = 
Окружность.
1)  AB = d, BC – хорда, d = 2r, AO = OB = r
AB = d, BC – хорда, d = 2r, AO = OB = r
C=2ПR, S= ПR2

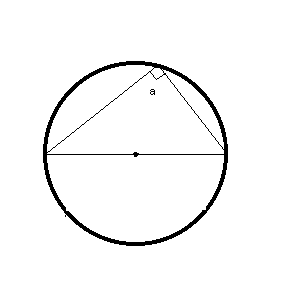 Ð a = 90
Ð a = 90 
Свойства:
а) Ð a(вписанный угол) = 
б) Ð b(центральный угол) = 
2) окружность, вписанная в треугольник:
а) разносторонний
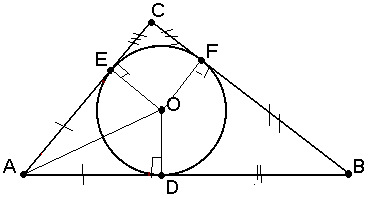
Свойство касательных к окружности:
Касательные, к окружности, проведенные из одной точки равны и образуют равные углы с прямой проходящей через эту точку и центр окружности.
б) равнобедренный
 AH – медиана, высота, биссектриса
AH – медиана, высота, биссектриса
т.О  AH
AH
в) равносторонний

AH, BM, CK – медиана, высота, биссектриса
т.О  AH, BM, CK
AH, BM, CK
3) окружность описанная около треугольника:
а) разносторонний б) равнобедренный в) равносторонний 


AH – медиана, высота, биссектриса
OH = r
Произведение отрезков одной хорды равно произведению отрезков другой хорды.
Не нашли, что искали? Воспользуйтесь поиском: