Относительная высота сжатой зоны бетона

, (4.7)

Здесь - коэффициент армирования или 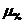- процент армирования, равный . Для упрощения вычислений в практических расчётах, формулы (4.3.) и (4.4.) преобразуют, вводя параметры и . Подставляя в них и переходя от неравенств к равенствам, получим

, (4.8)

, (4.9)

где ; .

Из формулы (4.8.) имеем . (4.10)

Из формулы (4.9.) . (4.11)

Полученные формулы справедливы при

. (4.12)

Все величины: 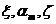связаны друг с другом; зная одну из них, можно по табл.4.1. найти любую другую. Рассмотрим 2-ой случай , т.е. . В этом случае элементы из бетона класса В30 и ниже с ненапрягаемой арматурой классов А-I, A-II, A-III, разрешается рассчитывать по формулам случая 1, подставляя в них значение . 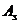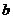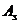Практически при расчёте прямоугольных сечений с одиночной арматурой могут встретиться три типа задач: определение площади растянутой арматуры ; подбор размеров поперечного сечения элемента и и арматуры ; проверка несущей способности сечения.

Таблица для расчета изгибаемых элементов прямоугольного сечения, армированных одиночной арматурой

Расчёт прочности нормальных сечений элементов прямоугольного профиля с двойной арматурой.

В сечениях с двойной арматурой рабочая арматура ставится как в растянутой, так и в сжатой зоне бетона. Необходимо отметить, что сечения с двойной арматурой являются неэкономичными. Они применяются тогда, когда сжатая арматура необходима для усиления сжатой зоны бетона (если по эксплуатационным или эстетическим требованиям высота сечения ограничена), т.е. разрушение элемента происходит по случаю 2, либо когда элемент подвергается действию знакопеременных моментов. Схема расчётных усилий, а также эпюра напряжений в поперечном сечении показаны на рис. 4.8. Здесь к усилию в сжатом бетоне добавляется усилие в сжатой арматуре , которое прикладывается на расстоянии от сжатой грани.

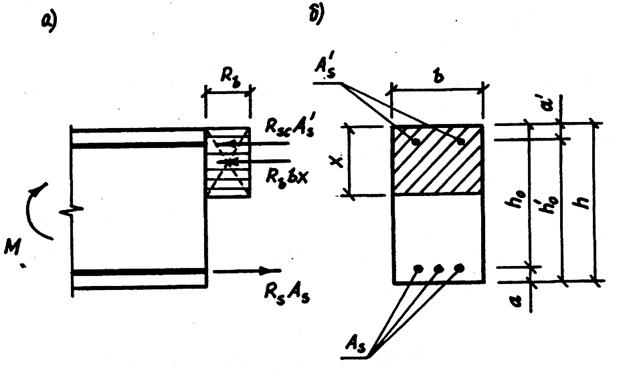
Рис. 4.8. Расчётная схема изгибаемого элемента с двойной арматурой

Условие прочности имеет вид

(4.13)

а уравнение проекций всех сил на продольную ось элемента

. (4.14)

Вводя параметры , перепишем (4.13.) и (4.14.) в виде

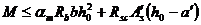, (4.13 а) . (4.14 а)

При этом имеется в виду соблюдение условия . Если же при одиночной арматуре получится, что 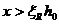, то в сжатой зоне бетона необходимо по расчёту поставить также сжатую арматуру.В этом случае для бетона класса В30 и ниже, а также арматуры класса не выше A-III расчёт можно производить по формуле (4.13 а), если вместо подставить . . (4.15)

В этой формуле 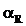определяют для значения , которое вычисляется по формуле (4.1). При расчёте сечений с двойной арматурой возможны задачи трёх типов: проверка несущей способности сечения; определение площади сечения сжатой и растянутой 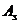арматуры; определение площади сечения растянутой арматуры 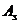, если известна площадь сечения сжатой арматуры .

Расчёт прочности нормальных сечений изгибаемых элементов таврового профиля. Такие сечения часто встречаются на практике либо в виде отдельных балок, либо в составе монолитных ребристых или сборных перекрытий (рис. 4.9.).

Рис. 4.9. Тавровые сечения

а – балка с полкой в сжатой зоне; б – то же в растянутой зоне; в – тавровое сечение в составе монолитного перекрытия; г – то же в составе сборного перекрытия; 1 – полка; 2 – сжатая зона; 3 – ребро.

Тавровые сечения с полкой в сжатой зоне в принципе выгоднее прямоугольных за счёт того, что сжатая зона бетона увеличивается, а растянутая зона практически неработающего бетона сокращается. Если полка таврового сечения находится в растянутой зоне, то она не увеличивает прочности элемента, однако иногда по конструктивным требованиям могут использоваться и такие сечения. Тавровые сечения, как правило, имеют одиночное армирование. Ширина свесов полки, которая учитывается в расчёте, ограничивается, поскольку участки полки, отдалённые от ребра, вовлекаются в работу меньше. Поэтому она принимается не более половины расстояния в свету между соседними ребрами и не более 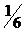пролёта рассчитываемого элемента, а в элементах с толщиной полки при отсутствии поперечных рёбер или с ребрами при расстоянии между ними более размера между продольными рёбрами, вводимая в расчёт ширина каждого свеса не должна превышать . При консольных свесах полки (для отдельных балок) указанные ограничения таковы: при 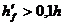- не более , при - не более ; при сечение рассматривается как прямоугольное, т.е. свесы вообще не учитывают. При расчёте тавровых сечений могут возникнуть два основных расчётных случая: нейтральная ось проходит в полке и нейтральная ось проходит в ребре (рис. 4.10.). Обычно нейтральная ось проходит в полке, т.е. тогда, когда свесы полки достаточно развиты, а количество растянутой арматуры невелико. В этом случае тавровое сечение рассчитывается как прямоугольное с размерами 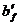х т.е. оно дополняется до прямоугольного (пунктир на рис.4.9,а). Такое дополнение допустимо, так как оно происходит за счёт неработающего растянутого бетона. При этом схема усилий и эпюра напряжений в сжатом бетоне остаются такими же, как и при расчёте прямоугольных сечений. Расчётными формулами являются

, (4.16)

. (4.17)

Преобразуя (4.16.), получим

(4.18)

где -коэффициент, определяемый по табл.4.1.

Рис. 4.10. Два расчетных случая тавровых сечений: расположение границы с жатой зоны в пределах полки и ниже полки

В некоторых случаях при слабо развитых свесах полки и достаточно большом армировании оказывается, что т.е. нейтральная ось смещается в ребро (рис. 4.10.). Таким образом сжатая зона сечения состоит из свесов полки и сжатой зоны ребра. Условие прочности можно записать на основании уравнения моментов относительно равнодействующей усилий в растянутой арматуре

. (4.19)

Учитывая соотношение , будем иметь

(4.19 а)

Положение нейтральной оси определяется из условия суммы проекций всех сил на продольную ось

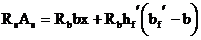(4.20) или (4.20 а)

Отметим, что всегда должно соблюдаться условие 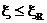. Расчёт таврового сечения производится в зависимости от того, по какому расчётному случаю работает заданное сечение. Разграничение случаев производится по следующим признакам:

1) известны все размеры сечения: , b, , h и задан расчётный изгибающий момент. Тогда если

, (4.21)

то нейтральная ось проходит в полке; при противоположном знаке неравенства она проходит в ребре;

2) известны все размеры сечения: , b, , h, а также A_s. Тогда если

(4.22)

то нейтральная ось проходит в полке; при обратном неравенстве она проходит в ребре. При расчёте тавровых сечений возможны задачи 2-х типов: проверка несущей способности сечения; определение площади сечения арматуры A_s.

Основная литература: 1[125-133, 138-147], 2[67-93], 4[205-212].

Дополнительная литература: 5[47-55, 58-59, 61-63], 7[78-93], 9[87-92].

Контрольные вопросы:

1. Какие требования предъявляются к конструированию изгибаемых железобетонных элементов (плит, балок)? Назначение продольной и поперечной арматуры?

2. Основные случаи разрушения железобетонной балки по нормальному к ее оси сечению. Условия, определяющие разрушение элемента по сжатой и растянутой зонам; от каких факторов они зависят?

3. Каковы предпосылки, принимаемые для расчета нормальных сечений с одиночной арматурой?

4. Вывод формул для расчета прямоугольных сечений изгибаемых элементов с одиночной арматурой.

5. Каковы особенности расчета переармированных сечений?

6. Как определить несущую способность по нормальному сечению элемента прямоугольного профиля с одиночной арматурой?

7. Какие характеристики используется для определения границы между двумя случаями расчета?

8. В каких случаях прибегают к установке двойной арматуры?

9. Выведите формулы для расчета прямоугольных сечений изгибаемых элементов с двойной арматурой?

10. Запишите условие, определяющее необходимость установки сжатой арматуры.

11. Где на практике встречаются тавровые сечения?

12. Почему ограничиваются расчетная ширина свесов полки, перечислите эти ограничения?

13. Назовите два основных расчетных случая таврового сечения и как определяется положение нейтральной оси в каждом из случаев?

14. Напишите условие, при котором тавровое сечение может рассматриваться как прямоугольное?

15. Выведите формулы для расчета таврового сечения.

Тема занятия 5. Расчёт прочности изгибаемых элементов по наклонным сечениям. Общие сведения. Изгибаемый элемент может разрушиться не только по сечению, нормальному к продольной оси балки, но и по наклонному сечению, расположенному вблизи опоры. Это происходит потому, что на приопорном участке действуют изгибающие моменты и довольно большие поперечные силы. В результате их совместного действия возникают главные сжимающие 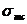и главные растягивающие напряжения, которые действуют под углом к оси элемента (рис. 5.1.).

Рис. 5.1. Главные напряжения в бетоне у опоры балки и разрушение изгибаемого элемента по наклонному сечению

Более опасными являются главные растягивающие напряжения. Как только 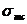превысят сопротивление бетона растяжению R_bt, образуются наклонные трещины (рис. 5.1.), которые при дальнейшем увеличении нагрузки раскрываются и происходит в конечной стадии разрушение. Элемент разрушается в результате того, что напряжения в поперечных стержнях (хомутах) достигают предельных значений, затем происходит раздробление бетона над вершиной наклонной трещины; при этом напряжения в продольной арматуре не всегда достигают предельных значений. Поскольку бетон хорошо работает на сжатие, то главные сжимающие напряжения опасны в основном в элементах с тонкой стенкой.

Расчёт на действие поперечной силы. При расчёте прочности наклонных сечений исходят из того условия, что усилия от внешних нагрузок в виде поперечной силы и изгибающего момента, которые действуют в наклонном сечении, не должны превышать внутренних предельных усилий в наклонном сечении. Однако такая методика, основанная на совместном учёте поперечных сил и изгибающих моментов, является весьма сложной и в настоящее время находится в стадии разработки. Поэтому в нормах принимается раздельный расчёт на действие поперечной силы и на действие изгибающего момента [13]. Расчётная схема усилий в наклонном сечении представлена на рис. 5.2. Здесь введены общепринятые обозначения: с - расстояние от вершины расчётного наклонного сечения до реакции опоры; с₀ - проекция расчётного сечения. Внутренние усилия в наклонном сечении следующие: продольные (N_b) и поперечные (Q_b) усилия в бетоне над наклонной трещиной; осевые усилия в продольной арматуре R_sA_s; осевые усилия в поперечной арматуре R_swA_sw, отогнутой арматуре R_swA_s,inc, пересекающих наклонную трещину.

Условие прочности наклонного сечения на действие поперечной силы записывается следующим образом , (5.1)

где Q – поперечная сила, действующая в вершине наклонного сечения от действия опорной реакции и нагрузки, расположенной на участке между опорой и вершиной наклонного сечения; Q_b – поперечное усилие, воспринимаемое бетоном сжатой зоны в вершине наклонного сечения; Q_sw – сумма осевых усилий в поперечных стержнях (хомутах), пересекаемых наклонным сечением; Q_s,inc - сумма проекций на нормаль к продольной оси элемента осевых усилий в отгибах, пересекаемых наклонным сечением.

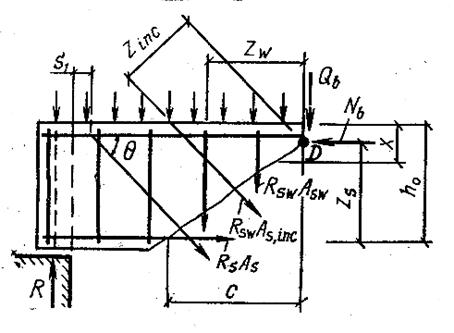
Рис. 5.2. К расчету изгибаемого элемента по наклонному сечению

Условие (5.1.) вытекает из уравнения проекций всех усилий. Оно основано на следующих предпосылках:

1. поперечная сила Q_b, воспринимаемая бетоном над наклонной трещиной, вычисляется в зависимости от расчётного сопротивления бетона растяжению R_bt, размеров элемента, а также наклона сечения. В общем случае она определяется по эмпирической формуле

(5.2)

где (5.3)

Q_b принимается не менее

(5.4)

Здесь - коэффициенты, которые принимаются в зависимости от вида бетона (табл. 5.1); - коэффициент, учитывающий сжатые полки таврового сечения:

,

причём величина принимается не более величины ; - коэффициент, учитывающий влияние продольной силы N (в частности усилия предварительного обжатия):

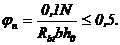
В формулах (5.3.) и (5.4.) принимают

Значения коэффициентов

Таблица 5.1.

Вид бетона
Тяжёлый		0,6	1,5
Мелкозернистый	1,7	0,5	1,2
Лёгкий при	1,9	0,5	1,2

2. Усилия в поперечной арматуре (хомутах) R_swA_sw и отогнутых стержнях R_swA_s,inc всегда направлены вдоль стержней. При этом в расчёт вводится только поперечная и отогнутая арматура, пересекаемая наклонным сечением. Усилие в продольной арматуре R_sA_s при расчёте на действие поперечной силы не учитывается. Величина для хомутов вычисляется по формулам

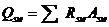или 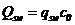, (5.5)

где q_sw – усилие в хомутах на единицу длины элемента, определяемое по формуле

. (5.6)

Здесь s – шаг хомутов; A_sw - площадь сечения хомутов в одной плоскости.

В формуле (5.5.) знак суммы относится только к тем поперечным стержням (хомутам), которые попали в проекцию с₀ наклонного сечения. Аналогично значение вычисляется по формуле

, (5.7)

где угол наклона отгибов к продольному направлению элемента.

Из формул (5.2.) и (5.5.) видно, что значения Q_b и Q_sw зависят от расстояния с и длины проекции наклонного сечения с₀. Первый член обратно пропорционален величине с, а второй член прямо пропорционален величине с₀, т.е. усилия в поперечных стержнях (хомутах), пересекаемых наклонным сечением, возрастают с увеличением проекции наклонного сечения.

Предположим, что отгибы отсутствуют, тогда условие прочности (5.1.) запишется в виде

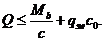(5.8)

При некотором значении с=с₀ суммарное усилие в правой части неравенства (5.8.) будет стремиться к минимуму, т.е.

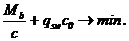(5.9)

Именно такую проекцию будет иметь наиболее опасная наклонная трещина, и из условия (5.9) определяется величина с₀

(5.10)

откуда . (5.11) Значение проекции опасной наклонной трещины должно быть не более, величины с и не более , а также не менее h₀, если c>h₀. Чтобы обеспечить прочность по наклонному сечению на участке между соседними хомутами должно выполняться условие

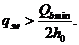(5.12)

Расстояние между хомутами s должно быть не более

(5.13)

Если на элемент действует равномерно распределённая нагрузка, то при q₁<0,56q_sw

(5.14)

в противном случае . (5.15)

При этом значение с должно удовлетворять неравенству

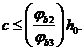(5.16)

Для тяжёлого бетона

(5.17)

В формулах (5.14), (5.15) значение q₁=q, где q – равномерно распределённая нагрузка. Если в неё включена временная равномерно распределённая нагрузка, то

(5.18)

где g – постоянная нагрузка; - временная нагрузка.

Поперечная сила в вершине наклонного сечения от внешней нагрузки

. (5.19)

здесь Q_max – поперечная сила на опоре.

Прочность по изгибающему моменту. Условие прочности наклонного сечения вытекает из того условия, что изгибающий момент М в наклонном сечении от расчётных нагрузок относительно точки приложения равнодействующей сжимающих усилий в сечении бетона над трещиной (рис.5.2.) не превышает суммы моментов внутренних расчётных усилий в продольных, поперечных и отогнутых стержнях относительно той же точки, т.е.

(5.20)

где

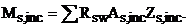
На действие изгибающего момента рассчитывают наклонные сечения в местах обрыва продольной арматуры в пролёте; у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров; в местах резкого изменения сечения.

Во многих случаях, как показывают исследования, условие прочности по изгибающему моменту в элементах постоянной или плавно изменяющейся высоты удовлетворяется без расчёта, при выполнении определённых конструктивных требований, а именно: 1) если обеспечена достаточная анкеровка арматуры на свободных опорах элемента; 2) если обеспечена достаточная анкеровка арматуры, обрываемой в пролёте. В этих случаях прочность наклонного сечения будет по крайней мере не ниже, чем прочность нормального сечения этой же балки.

Прочность бетона по наклонной сжатой полосе. Бетон между наклонными трещинами испытывает одновременно воздействие главных сжимающих напряжений и растягивающих усилий в поперечных стержнях (хомутах) (рис. 5.3), т.е. находится в условиях двухосного напряжённого состояния: сжатие – растяжение. В этом случае прочность бетона будет ниже, чем при одноосном напряженном состоянии.

Рис. 5.3. К расчету прочности бетона по наклонной сжатой полосе

Согласно практическим рекомендациям, для элементов прямоугольного, таврового, двутаврового профилей для обеспечения прочности бетона на сжатие в полосе между наклонными трещинами должно выполняться условие

(5.21)

Здесь – коэффициент, учитывающий влияние поперечных стержней (хомутов) балки , 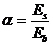; , , A_swi – площадь сечения одного хомута; n - число хомутов в сечении элемента; s - расстояние между хомутами; - коэффициент, равный 0,01 для тяжёлого и мелкозернистого бетона, 0,02 - для легкого бетона; R_b- сопротивление бетона сжатию (МПа).

Если условие (5.21.) не выполняется, необходимо увеличить размеры сечения балки, либо повысить класс бетона.

Расчёт прочности наклонных сечений элементов без поперечной арматуры. В балках, сплошных плитах высотой менее 150 мм, в многопустотных плитах высотой менее 300 мм и т.п. допускается поперечную арматуру не устанавливать [13]. Однако при этом необходимо произвести расчёт на действие поперечной силы. Расчёт элементов без поперечной арматуры на действие поперечных сил имеет некоторые особенности, которые связаны с условиями образования и развития в них наклонных трещин. В этом случае расчёт прочности по наклонным сечениям производят по двум эмпирическим формулам

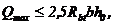(5.22)

(5.23)

Здесь значение коэффициента 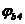определяется по табл. 5.1. При этом

При равномерно распределённой нагрузке и выполнении условия

(5.24)

принимают 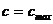; если условие (5.24.) не выполняется, то значение с принимают равным

. (5.25)

Если не выполняется хотя бы одно из условий (5.22.) или (5.23) необходима установка поперечной арматуры по расчету.

Основная литература: 1[150-158], 2[93-100], 4[214-220].

Дополнительная литература: 5[67-75], 7[96-106], 9[92-99].

Контрольные вопросы:

1. Что вызывает образование наклонных трещин на приопорных участках изгибаемых элементов? Каковы схемы разрушения по наклонным сечениям?

2. Каково условие прочности элемента по наклонному сечению на действие поперечной силы, изгибающего момента?

3. Какие существуют технологического требования по наименьшему диаметру поперечных стержней (хомутов) и конструктивные требования по наибольшему расстоянию между ними?

4. Чему равна поперечная сила 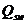, воспринимаемая хомутами, в расчетном наклонном сечении?

5. От чего зависит поперечная сила , воспринимаемая бетоном сжатой зоны над наклонным сечением?

6. Как записать условия прочности по наклонному сечению в балках с поперечной арматурой?

7. Как записать условия прочности по наклонному сечению в балках без поперечной арматурой?

8. Как выполняют проверку на действие поперечной силы по наклонной сжатой полосе?

Не нашли, что искали? Воспользуйтесь поиском: