Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

На рисунке показаны все три перпендикуляра.

Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.

Вот как все это выглядит в пространстве:

На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

Теорема о трех перпендикулярах — полезный инструмент для решения задач.
Например, с ее помощью можно доказать, что диагональ куба АС₁ перпендикулярна прямой BD:

Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:

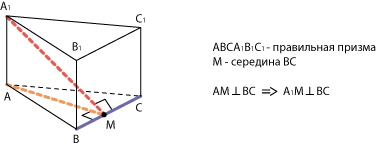
Или — что в правильной треугольной призме прямая А₁М (где М — середина ВС) перпендикулярна ребру ВС.

Не нашли, что искали? Воспользуйтесь поиском: