Объём и его измерение.

Величина части пространства, занимаемая геометрическим телом, называется объемом этого тела.

Вычислить объем (или измерить объем) означает найти положительное число, показывающее, сколько единиц измерения объемов и частей единицы содержится в данном теле.

За единицу измерения объема принимают объем куба, ребро которого равно единице измерения длины ( и т. д.).

Свойства объемов

1. Равные тела имеют равные объемы.
2. Если тело составлено из нескольких тел, попарно не имеющих общих внутренних точек, то его объем равен сумме объемов этих тел.
3. Объем куба равен кубу его ребра.

Многогранники, имеющие равные объемы называются равновеликими.

Теорема 1.

Объем прямоугольного параллелепипеда равен произведению трех его измерений.

Теорема 2

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.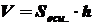

Теорема 3

Объем прямой призмы равен произведению площади основания на высоту.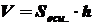

Теорема 4

Объем наклонной призмы равен произведению площади основания на высоту.

Теорема 5

Объем пирамиды равен одной трети произведения площади основания на высоту.

Теорема 6

Объем усеченной пирамиды, высота которой равна 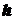, а площади оснований и , вычисляется по формуле .

Формулы вычисления объема тел вращения можно получить, используя определенный интеграл: .

Например, получим формулу для вычисления объема шара:

.

Аналогично получены формулы:

Теорема 7

Объем прямого цилиндра равен произведению площади основания на высоту.

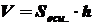
Теорема 8

Объем конуса равен одной трети произведения площади основания на высоту.

Теорема 9

Объем усеченного конуса, высота которого равна 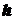, а площади оснований и , вычисляется по формуле .

Теорема 10

Объем шара радиуса равен .

Не нашли, что искали? Воспользуйтесь поиском: