
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Когда данное число лежит между корнями квадратного уравнения
Расположение корней квадратного трехчлена
 |
Для решения такой задачи не нужно находить корни уравнения и составлять двойное неравенство. Рассмотрим параболу с ветвями, направленными вверх (рис. 1). Понятно, что в промежутке между корнями лежат те и только те точки
 , в которых квадратичная функция принимает отрицательные значения. Если же ветви направлены вниз (рис. 2), то между корнями лежат точки, в которых функция принимает положительные значения. Поэтому удовлетворять условию задачи будут такие значения параметра, которые являются решениями либо системы
, в которых квадратичная функция принимает отрицательные значения. Если же ветви направлены вниз (рис. 2), то между корнями лежат точки, в которых функция принимает положительные значения. Поэтому удовлетворять условию задачи будут такие значения параметра, которые являются решениями либо системы  , либо системы
, либо системы  . Вместо двух систем можно записать одно неравенство:
. Вместо двух систем можно записать одно неравенство:  .
.
1. При каких значениях  число –2 лежит между корнями уравнения
число –2 лежит между корнями уравнения  Решение. Составим неравенство
Решение. Составим неравенство  . Для этого найдем
. Для этого найдем  . Получим неравенство
. Получим неравенство 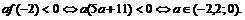 Ответ:
Ответ:  .
.
2. При каких  корни уравнения
корни уравнения  удовлетворяют условию
удовлетворяют условию 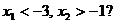 Решение. Эта задача представляет собой немного усложненный вариант предыдущей задачи. Здесь между корнями должны лежать две точки, а не одна. Значит, включаем в систему два неравенства:
Решение. Эта задача представляет собой немного усложненный вариант предыдущей задачи. Здесь между корнями должны лежать две точки, а не одна. Значит, включаем в систему два неравенства:  , или
, или  . Изображаем решения неравенств на двух числовых прямых (рис. 3). Ответ:
. Изображаем решения неравенств на двух числовых прямых (рис. 3). Ответ:  .
.
3.
 |
При каких положительных значениях
 неравенство
неравенство 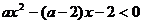 является следствием неравенства
является следствием неравенства  ? Решение. Вспомним, что означает слова «неравенство (1) является следствием неравенства (2)», или «неравенство (1) следует из неравенства (2)». Это означает следующее: если
? Решение. Вспомним, что означает слова «неравенство (1) является следствием неравенства (2)», или «неравенство (1) следует из неравенства (2)». Это означает следующее: если  удовлетворяет неравенству (2), то это значение
удовлетворяет неравенству (2), то это значение  удовлетворяет и неравенству (1), то есть множество решений неравенства (2) входит во множество решений неравенства (1). Итак, множество решений неравенства
удовлетворяет и неравенству (1), то есть множество решений неравенства (2) входит во множество решений неравенства (1). Итак, множество решений неравенства  , т. е. промежуток
, т. е. промежуток  , содержится во множестве решений неравенства
, содержится во множестве решений неравенства 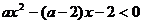 . Так как по условию
. Так как по условию  , то ветви параболы направлены вверх, и решение данного неравенства – это интервал между корнями уравнения
, то ветви параболы направлены вверх, и решение данного неравенства – это интервал между корнями уравнения  . Значит, задача сводится к тому, что числа 1 и –1 должны лежать между корнями данного уравнения или с ними совпадать. Так как старший коэффициент положителен, то получаем два условия:
. Значит, задача сводится к тому, что числа 1 и –1 должны лежать между корнями данного уравнения или с ними совпадать. Так как старший коэффициент положителен, то получаем два условия:  . Первое условие выполняется для любых
. Первое условие выполняется для любых  :
:  . Решаем неравенство
. Решаем неравенство 
 . Ответ:
. Ответ:  .
.
4. При каких  из неравенства
из неравенства 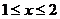 следует неравенство
следует неравенство  ? Решение. Условие означает, что для всех
? Решение. Условие означает, что для всех  выполняется неравенство
выполняется неравенство  , т. е. отрезок
, т. е. отрезок 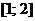 лежит между корнями уравнения
лежит между корнями уравнения  . Так как старший коэффициент в данном случае положителен, то достаточно, чтобы выполнялись неравенства
. Так как старший коэффициент в данном случае положителен, то достаточно, чтобы выполнялись неравенства  . Получаем систему
. Получаем систему  . Ответ:
. Ответ: 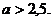
5. При каких  неравенство
неравенство  выполняется для всех
выполняется для всех  ? Решение. Данное неравенство равносильно неравенству
? Решение. Данное неравенство равносильно неравенству  . Так как старший коэффициент в данном случае положителен, то отрезок
. Так как старший коэффициент в данном случае положителен, то отрезок 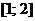 должен лежать между корнями уравнения
должен лежать между корнями уравнения  , а для этого достаточно, чтобы выполнялись неравенства
, а для этого достаточно, чтобы выполнялись неравенства  . Получаем систему
. Получаем систему 


 . Ответ:
. Ответ:  .
.
Когда корни уравнения лежат по одну сторону от данного числа 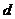
Здесь также существует схема решения, не требующая нахождения корней, но она довольно громоздкая. При положительном старшем коэффициенте (рис. 4) требуем, чтобы 1) в точке 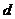 функция была положительной:
функция была положительной:  2) абсцисса вершины параболы лежала по ту же сторону от числа
2) абсцисса вершины параболы лежала по ту же сторону от числа 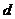 , что и корни; 3) корни существовали, т. е. выполнялось условие
, что и корни; 3) корни существовали, т. е. выполнялось условие  . В случае отри
. В случае отри  цательного старшего коэффициента (рис. 5) условие 1) заменяем на противоположное:
цательного старшего коэффициента (рис. 5) условие 1) заменяем на противоположное:  . Если не требуется, чтобы корни были обязательно различными, то отдельно надо разобрать случай, когда старший коэффициент равен 0. При этом находим корень и выясняем его положение относительно числа
. Если не требуется, чтобы корни были обязательно различными, то отдельно надо разобрать случай, когда старший коэффициент равен 0. При этом находим корень и выясняем его положение относительно числа  Таким образом, если старший коэффициент зависит от параметра, то приходится решать две системы, содержащие по четыре неравенства, что представляет собой немалую работу:
Таким образом, если старший коэффициент зависит от параметра, то приходится решать две системы, содержащие по четыре неравенства, что представляет собой немалую работу:  или
или  . Правда, эти две системы можно объединить в одну, заменив первое и третье неравенства одним:
. Правда, эти две системы можно объединить в одну, заменив первое и третье неравенства одним:  , т. е. решать систему
, т. е. решать систему 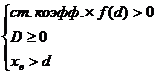 . В каждом конкретном случае нужно подумать, не проще ли найти корни и решить соответствующие неравенства. Есть смысл это сделать в двух случаях. Во-первых, когда дискриминант является полным квадратом, и, следовательно, корни не содержат радикалов. Во-вторых, когда старший коэффициент не зависит от параметра. В этом случае сразу известно, какой из корней больше: тот, в котором радикал со знаком «+». Поэтому придется решать только одно неравенство: если требуется, чтобы оба корня были меньше числа
. В каждом конкретном случае нужно подумать, не проще ли найти корни и решить соответствующие неравенства. Есть смысл это сделать в двух случаях. Во-первых, когда дискриминант является полным квадратом, и, следовательно, корни не содержат радикалов. Во-вторых, когда старший коэффициент не зависит от параметра. В этом случае сразу известно, какой из корней больше: тот, в котором радикал со знаком «+». Поэтому придется решать только одно неравенство: если требуется, чтобы оба корня были меньше числа 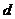 , то меньше
, то меньше 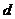 должен быть больший корень, если оба корня больше
должен быть больший корень, если оба корня больше 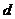 , то больше
, то больше 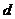 должен быть меньший корень. В некоторых случаях применим и третий способ решения. Он состоит в следующем: из уравнения выражаем параметр и стоим график полученной функции. Абсциссы точек пересечения этого графика и прямой
должен быть меньший корень. В некоторых случаях применим и третий способ решения. Он состоит в следующем: из уравнения выражаем параметр и стоим график полученной функции. Абсциссы точек пересечения этого графика и прямой 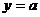 — это корни исходного уравнения при данном значении
— это корни исходного уравнения при данном значении  . По графику обычно бывает видно, при каких значениях параметра корни расположены нужным образом. Способ удобно применять тогда, когда параметр достаточно просто выражается через
. По графику обычно бывает видно, при каких значениях параметра корни расположены нужным образом. Способ удобно применять тогда, когда параметр достаточно просто выражается через  . Особенно эффективен этот способ в задачах с набором из нескольких условий.
. Особенно эффективен этот способ в задачах с набором из нескольких условий.
Иногда в задачах этого типа требуется, чтобы корни были обязательно различными. Тогда в системе 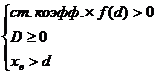 заменяем неравенство
заменяем неравенство  на
на  .
.
6. При каких  корни уравнения
корни уравнения  больше
больше  ? Решение. Воспользуемся схемой. Получим систему неравенств
? Решение. Воспользуемся схемой. Получим систему неравенств 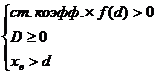 , имеющую вид
, имеющую вид 
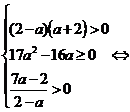


 В условии задачи не говорится, что корни должны быть различны, поэтому мы не исключили случай, когда
В условии задачи не говорится, что корни должны быть различны, поэтому мы не исключили случай, когда  . Не забудем также случай, когда старший коэффициент равен 0:
. Не забудем также случай, когда старший коэффициент равен 0:  . Значит, данное значение параметра не подходит. Ответ:
. Значит, данное значение параметра не подходит. Ответ: 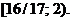
Заметим, что решение, использующее нахождение корней, здесь выглядит менее рациональным. Решая уравнение при  , получаем
, получаем  . Решать два иррациональных неравенства, да еще с переменным знаменателем — большая работа.
. Решать два иррациональных неравенства, да еще с переменным знаменателем — большая работа.
7. При каких значениях  оба корня уравнения
оба корня уравнения  больше 3? Решение. Найдем корни уравнения:
больше 3? Решение. Найдем корни уравнения: 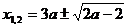 . Здесь уже есть смысл решить иррациональное неравенство. Достаточно потребовать, чтобы меньший корень был больше 3:
. Здесь уже есть смысл решить иррациональное неравенство. Достаточно потребовать, чтобы меньший корень был больше 3: 


 . Из формулировки неясно, «оба корня» — это обязательно различные корни, или допустимы и равные корни. Но в данном случае равные корни получаются при
. Из формулировки неясно, «оба корня» — это обязательно различные корни, или допустимы и равные корни. Но в данном случае равные корни получаются при  , а это значение все равно не вошло в ответ, так что можем над этим вопросом не задумываться. Ответ:
, а это значение все равно не вошло в ответ, так что можем над этим вопросом не задумываться. Ответ:  .
.
8. При каких  оба корня уравнения
оба корня уравнения  принадлежат отрезку
принадлежат отрезку  ? Решение. Приведем решение «по схеме»:
? Решение. Приведем решение «по схеме»: 



 . Равные корни получаются при
. Равные корни получаются при 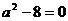 . Поскольку опять неясно, обязательно ли корни различны, запишем ответ следующим образом: при
. Поскольку опять неясно, обязательно ли корни различны, запишем ответ следующим образом: при  в отрезке
в отрезке  лежат два различных корня уравнения, при
лежат два различных корня уравнения, при  уравнение имеет кратный корень
уравнение имеет кратный корень  , лежащий в этом отрезке. Ответ: при
, лежащий в этом отрезке. Ответ: при  два различных корня, при
два различных корня, при  кратный корень.
кратный корень.
9. При каких  корни уравнения
корни уравнения 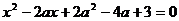 удовлетворяют неравенствам
удовлетворяют неравенствам  ? Решение. Условие
? Решение. Условие  будет выполнено тогда и только тогда, когда
будет выполнено тогда и только тогда, когда  , где
, где  . При этом проверки существования корней производить не нужно, они обязательно существуют. Таким образом, получаем неравенство
. При этом проверки существования корней производить не нужно, они обязательно существуют. Таким образом, получаем неравенство 

 . Условие
. Условие  проще записать непосредственно:
проще записать непосредственно:  . Решая это неравенство, получаем
. Решая это неравенство, получаем 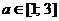 . Окончательно,
. Окончательно,  . Ответ:
. Ответ:  .
.
10. При каких  оба корня уравнения
оба корня уравнения  лежат в промежутке (–4; 0)? Решение. Рассмотри на данном примере все три способы решения.
лежат в промежутке (–4; 0)? Решение. Рассмотри на данном примере все три способы решения.
Выделение параметра. Решив уравнение относительно  , получим
, получим  . Построим график функции
. Построим график функции  (рис. 6). Преобразуем функцию таким образом:
(рис. 6). Преобразуем функцию таким образом:  . Находим нули функции:
. Находим нули функции:  , значение в точке 0
, значение в точке 0  . Проводим вертикальную асимптоту
. Проводим вертикальную асимптоту 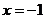 . Найдем производную
. Найдем производную 
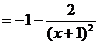 . Так как
. Так как  производная отрицательна во всех точках области определения, то функция убывает на промежутках
производная отрицательна во всех точках области определения, то функция убывает на промежутках  и
и  . Вычислим значение
. Вычислим значение  . По чертежу видно, что оба корня уравнения
. По чертежу видно, что оба корня уравнения  лежат в промежутке (–4; 0) тогда и только тогда, когда
лежат в промежутке (–4; 0) тогда и только тогда, когда  .
.
1) Нахождение корней. Решим уравнение:  . Потребуем, чтобы больший корень был меньше 0, а меньший — больше –4. Получим систему неравенств
. Потребуем, чтобы больший корень был меньше 0, а меньший — больше –4. Получим систему неравенств 

 . Решаем отдельно первое неравенство системы: оно равносильно системе:
. Решаем отдельно первое неравенство системы: оно равносильно системе: 
 . Решение второго неравенства
. Решение второго неравенства 
 . Получаем систему
. Получаем систему 
 .
.
2) Решение «по схеме». Для нужного расположения корней потребуем 1) чтобы вершина параболы лежала между точками –4 и 0; 2) чтобы значения функции  в точках –4 и 0 были положительны; 3) чтобы корни существовали. Получим систему
в точках –4 и 0 были положительны; 3) чтобы корни существовали. Получим систему 
 . Ответ:
. Ответ:  .
.
11. При каких  уравнение
уравнение  имеет хотя бы один корень меньше 1? Решение. Решим эту задачу также тремя способами.1) Непосредственное нахождение корней. Решаем уравнение:
имеет хотя бы один корень меньше 1? Решение. Решим эту задачу также тремя способами.1) Непосредственное нахождение корней. Решаем уравнение: 

 . По условию меньший корень должен быть меньше 1. Решаем неравенство
. По условию меньший корень должен быть меньше 1. Решаем неравенство 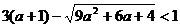

 , равносильное совокупности двух систем:
, равносильное совокупности двух систем: 

 . Ответ:
. Ответ: 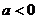 .
.
2) Решение «по схеме». Сложность в том, что в данном случае постановка задачи не соответствует нашей «схеме». Поэтому мы сначала ответим на другой, противоположный вопрос: при каких  уравнение не имеет ни одного корня меньше 1? Это возможно в двух случаях: во-первых, когда корней нет вообще, во-вторых, когда все корни больше или равны 1. Найдем дискриминант:
уравнение не имеет ни одного корня меньше 1? Это возможно в двух случаях: во-первых, когда корней нет вообще, во-вторых, когда все корни больше или равны 1. Найдем дискриминант:  . Так как уравнение
. Так как уравнение  не имеет корней, то для всех
не имеет корней, то для всех 
 , следовательно, уравнение
, следовательно, уравнение  имеет корни при всех значениях
имеет корни при всех значениях  . Теперь рассмотрим, когда все корни больше или равны 1. Получим систему
. Теперь рассмотрим, когда все корни больше или равны 1. Получим систему  (условие
(условие  уже не включаем в систему, так как знаем, что оно всегда выполняется). Итак, решаем систему
уже не включаем в систему, так как знаем, что оно всегда выполняется). Итак, решаем систему 
 . Итак, все корни больше или равны 1 при
. Итак, все корни больше или равны 1 при  . Так как при любых
. Так как при любых  корни существуют, то при
корни существуют, то при 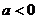 хотя бы один корень меньше 1. Ответ:
хотя бы один корень меньше 1. Ответ: 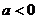 .
.
3) Выделение параметра. Выражаем из уравнения параметр:  . Строим график данной функции (рис. 7). Находим нули функции:
. Строим график данной функции (рис. 7). Находим нули функции:  , значение в точке 0
, значение в точке 0  . Проводим вертикальную асимптоту
. Проводим вертикальную асимптоту  . Найдем производную
. Найдем производную 
 . Так как производная положительна во всех точках области оп
. Так как производная положительна во всех точках области оп  ределения, то функция возрастает на промежутках
ределения, то функция возрастает на промежутках  и
и  . На графике изображена еще одна, наклонная, асимптота
. На графике изображена еще одна, наклонная, асимптота 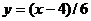 , но для решения задачи ее изображение не обязательно. По графику видно, что при
, но для решения задачи ее изображение не обязательно. По графику видно, что при 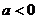 имеется корень меньше 1. Ответ:
имеется корень меньше 1. Ответ: 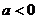 .
.
12. При каких  корни уравнения
корни уравнения  по абсолютной величине не превосходят 1? Решение. В данном случае проще решить это уравнение:
по абсолютной величине не превосходят 1? Решение. В данном случае проще решить это уравнение:  Получаем
Получаем  . Случай, когда
. Случай, когда  , нужно рассмотреть отдельно: получаем при этом
, нужно рассмотреть отдельно: получаем при этом  , т. е. значение
, т. е. значение  подходит. Ответ:
подходит. Ответ: 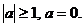
13. При каких  уравнение
уравнение  имеет хотя бы одно решение больше 1? Решение. Решим уравнение при
имеет хотя бы одно решение больше 1? Решение. Решим уравнение при  :
: 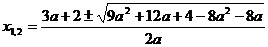
 ,
,  . Значит, должно выполняться неравенство
. Значит, должно выполняться неравенство 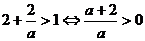

 . Отдельно рассматриваем случай
. Отдельно рассматриваем случай 
 . Ответ:
. Ответ: 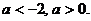
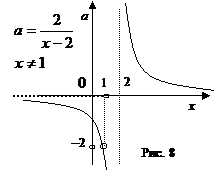 Приведем другое решение. Можно выразить
Приведем другое решение. Можно выразить 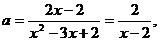
 . По графику (рис. 8) видно, что решений, не превосходящих 1, нет только при
. По графику (рис. 8) видно, что решений, не превосходящих 1, нет только при  . Ответ:
. Ответ: 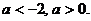
14.  При каких
При каких  уравнение
уравнение  имеет в промежутке
имеет в промежутке  а) хотя бы один корень; б) ровно один корень; в) два различных корня? Решение. В данном случае гораздо выгоднее решение, основанное на выделении параметра, поскольку параметр выражается очень просто: как квадратичная функция от
а) хотя бы один корень; б) ровно один корень; в) два различных корня? Решение. В данном случае гораздо выгоднее решение, основанное на выделении параметра, поскольку параметр выражается очень просто: как квадратичная функция от  . Строим график функции
. Строим график функции  (рис. 9). Так как
(рис. 9). Так как  а наименьшее значение функции равно
а наименьшее значение функции равно  , то получаем такой ответ: а)
, то получаем такой ответ: а)  б
б  в)
в) 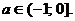 Ответ: а)
Ответ: а)  б)
б)  в)
в) 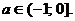
15. При каких  уравнение
уравнение  имеет корни
имеет корни  Решение. Проще решить уравнение относительно
Решение. Проще решить уравнение относительно 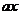 :
: 
 . Отсюда
. Отсюда  , или
, или  Ответ:
Ответ:  .
.
16. При каких  решения системы
решения системы  удовлетворяют условию
удовлетворяют условию  Решение. Задача равносильна следующей: при каких
Решение. Задача равносильна следующей: при каких  корни уравнения
корни уравнения  лежат в промежутке (–1; 1)? Уравнение
лежат в промежутке (–1; 1)? Уравнение  можно решить относительно
можно решить относительно  :
:  . Отсюда
. Отсюда 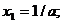
 Ответ:
Ответ:  .
.
17. При каких значениях  неравенство
неравенство 
 выполняется хотя бы при одном
выполняется хотя бы при одном  из отрезка
из отрезка  ? Решение. Рассмотрим неравенство как квадратное относительно
? Решение. Рассмотрим неравенство как квадратное относительно  :
: 
 . Проще сначала ответить на противоположный вопрос: при каких
. Проще сначала ответить на противоположный вопрос: при каких  неравенство
неравенство 


 неверно на всем отрезке
неверно на всем отрезке  , или
, или 
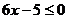 на всем отрезке
на всем отрезке  . Мы знаем, что для этого нужно потребовать выполнения неравенства на концах отрезка:
. Мы знаем, что для этого нужно потребовать выполнения неравенства на концах отрезка: 

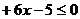 и
и 

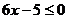 . Преобразовав этим неравенства, получим
. Преобразовав этим неравенства, получим 
 и
и 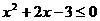
 , т. е.
, т. е.  . Нам же нужно взять остальные значения:
. Нам же нужно взять остальные значения: 
 . Ответ:
. Ответ:  .
.
Не нашли, что искали? Воспользуйтесь поиском: