
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| Формула Ньютона-Лейбница.
Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции  , то , то 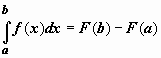
|
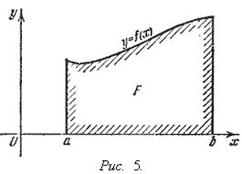
Геометрический смысл определенного интеграла.
Если f(x) непрерывна и положительна на [a, b], то интеграл  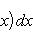 представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x).
Если фигура ограничена сверху и снизу неотрицательными функциями представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x).
Если фигура ограничена сверху и снизу неотрицательными функциями 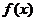 и и 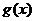 соответственно, непрерывными на отрезке [a, b], то площадь криволинейной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху графиками функций соответственно, непрерывными на отрезке [a, b], то площадь криволинейной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху графиками функций 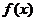 и и 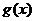 : : 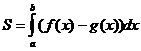 . .
|
Не нашли, что искали? Воспользуйтесь поиском: