Переходные процессы в цепи, состоящей из емкости и сопротивления

Подключим незаряженный конденсатор, емкостью 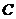, через резистор, сопротивлением 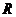к источнику питания с постоянным напряжением 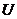(ключ 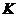находится в положении 1), см. рис. 1.

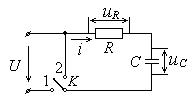
Рис. 1. Последовательная RC-цепь

Известно, что напряжение на зажимах конденсатора пропорционально заряду на его пластинах 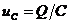. Если конденсатор не заряжен, то напряжение на нем в момент подключения к источнику напряжения, равно нулю (на рис. 1 ключ К переводится в положение 1). То есть 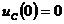. Далее конденсатор начинает заряжаться. После окончания заряда (достижение установившегося режима) напряжение на нем равно напряжению источника питания, то есть .

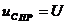Во время заряда конденсатора напряжение на нем равно сумме двух составляющих: напряжения принужденного режима 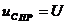и напряжения свободного режима т.е.

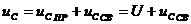(1)

Используя второй закон Кирхгофа, запишем:

.

Так как ток 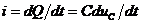, то уравнение данной цепи будет иметь вид:

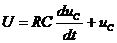(2)

С учетом (1) и (2), можно записать:

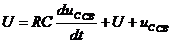(3)

Из последнего уравнения для свободного режима получаем:

.

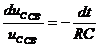Величина 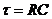называется постоянной времени цепи (имеет размерность времени). Чем больше 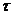, тем медленнее процесс и наоборот. Следовательно, 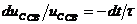. Интегрируя уравнение почленно, найдем

,

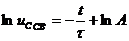откуда

.

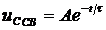Постоянную интегрирования 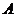определим из начальных условий. При 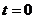, согласно второму закону коммутации, 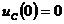. Тогда 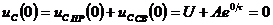, откуда 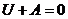или .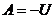

Таким образом, в процессе заряда конденсатора напряжение на нем изменяется по закону:

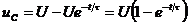. (4)

Ток переходного режима, или зарядный ток будет определяться выражением:

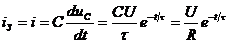. (5)

Падение напряжения на сопротивлении 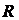будет изменяться пропорционально току:

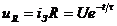(6)

Из формул (4), (5) и (6) видно, что при 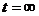ток заряда 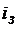и напряжение 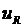стремятся к нулю, а напряжение 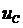– к значению напряжения 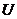. За время, равное одной постоянной времени цепи 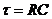, конденсатор зарядится только до величины 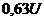(при этом зарядный ток уменьшится в 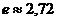раза). Практически считают, что конденсатор зарядился и переходный процесс закончился, если напряжение на нем достигло значения 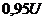. Это произойдет через время, равное трем постоянным времени цепи: .

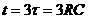Если после заряда конденсатора (в момент времени 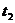, рис. 2) перевести ключ 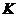в положение 2 (рис. 1), то заряженный конденсатор 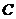окажется замкнутым на резистор 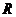, а в цепи начнет протекать ток разряда конденсатора 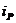. Напряжение на зажимах цепи также, как и в предыдущем случае, равно сумме напряжений на емкости 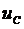и на сопротивлении 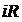, то есть:

.

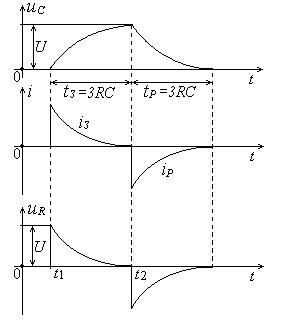
Рис. 2. Диаграмма напряжений и тока в RC-цепи

Но, так как в этом случае в цепи нет источника питания, то будут иметь место равенства:

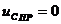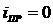, и , .

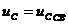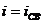Согласно второму закону Кирхгофа, уравнение цепи будет иметь вид: , или ,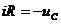

а ток в цепи

(7)

Знак минус показывает, что при разряде конденсатора ток в цепи направлен обратно тому положительному направлению, которое показано на рис. 1, и обратно току заряда конденсатора .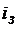

Так как ток 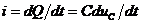, то уравнение цепи, с учетом (7), примет вид:

,

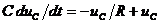откуда получаем дифференциальное уравнение для напряжения на конденсаторе:

.

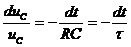Интегрируя правую и левую части уравнения, получим:

.

Из этого выражения следует, что

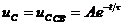. (8)

Постоянную 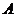также найдем из начальных условий. Согласно второму закону коммутации в начальный момент времени разряда конденсатора 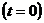напряжение остается таким же, как до переключения ключа 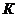, т.е. 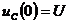, и, в соответствии с (8), 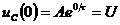. Следовательно .

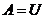Таким образом, напряжение на конденсаторе при его разряде: 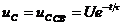, (9)

а разрядный ток в цепи:

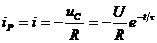. (10)

Напряжение на конденсаторе в начальный момент времени разряда (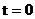) имеет наибольшее значение, а затем изменяется по закону показательной функции, достигая по прошествии времени 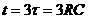практически нулевого значения (0,05 первоначального напряжения на нем). Ток в контуре в момент 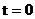скачком изменяется от нуля до значения 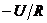, а затем изменяется пропорционально напряжению на конденсаторе. Скорость протекания процесса, как и в предыдущем случае, определяется постоянной времени . Данные рассуждения поясняются временными диаграммами напряжения и тока, приведенными на рис. 2.

1.1.2. Дифференцирующая RC–цепь

Дифференцирующей цепью называется линейная цепь, для которой в общем случае выходной сигнал 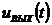связан с входным сигналом 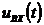соотношением:

, где 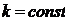. (11)

На рис. 3 приведена RC–цепь, которая может быть дифференцирующей, при условии, что для нее постоянная времени 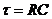много меньше характерного временного интервала входного сигнала, в данном случае длительности импульса (т. е. выполняется условие t<<t_И). При этом для

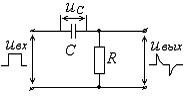
Рис. 3. Дифференцирующая RC-цепь (t_И>3RC)

нее справедливо выражение:

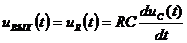, (12)

При воздействии этого импульса конденсатор С будет заряжаться. На резисторе 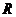сначала возникнет импульс, срез которого является экспоненциальной кривой с постоянной времени 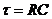. Этот импульс имеет ту же полярность, что и прямоугольный входной импульс. При окончании действия входного импульса на выходе цепи появится второй импульс, убывающий по модулю с той же постоянной времени, полярность которого будет противоположна полярности входного импульса. Эти выходные импульсы связаны с процессом заряда и разряда конденсатора соответственно (см. рис. 4).

Для повышения качества дифференцирования (получения более коротких импульсов) на выходе ДЦ необходимо уменьшить постоянную времени 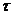. Од-нако уменьшать 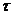можно только до определенного предела. Из-за влияния па-

Рис. 4. Диаграммы напряжений на элементах цепи рис. 3

для случая t_И>3RC

разитных параметров цепи (паразитных емкостей и внутреннего сопротивления источника) и из-за того, что фронт и срез входного импульса имеют определенную длительность (входные импульсы имеют практически не прямоугольную, а трапецеидальную форму), уменьшение 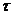сверх некоторого предела вызывает лишь убывание амплитуды выходных импульсов без значительного сокращения их длительности.

В случае, когда постоянная времени цепи 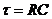больше длительности входного импульса 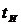, он закончится раньше завершения процесса заряда конденсатора (см. рис. 5). В момент окончания прямоугольного импульса напряжение на конденсаторе 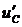будет меньше амплитуды импульса 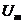. Напряжение на выходе цепи 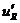будет равно разности амплитуды импульса и напряжения на конденсаторе: 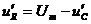. В момент окончания прямоугольного импульса на входе цепи появится отрицательный скачок напряжения на резисторе 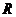, равный 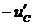. Напряжение на сопротивлении при этом изменится скачком от 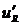до 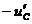т.е. на величину: 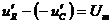. Затем происходит разряд конденсатора. Если при этом постоянную време-

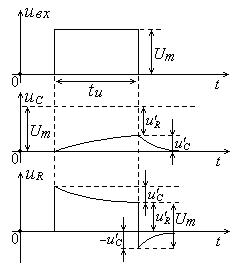
Рис. 5. Диаграммы напряжений на элементах цепи рис. 3

для случая t_И<3RC

ни цепи увеличивать, то напряжение 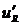будет приближаться к значению 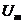, а напряжение 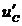– к нулевому значению. В этом случае RC–цепь дифференцирующей уже не является.

При очень большой величине 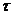прямоугольный импульс пройдет через RC-цепь почти без искажений, так как за время импульса напряжение на конденсаторе не успевает измениться, и импульс на резисторе практически повторяет по форме импульс на входе. В этом случае RC-цепь дифференцирующей также не является, а называется переходной (разделительной).

Дифференцирующие цепи чаще всего применяются в импульсных схемах для формирования кратковременных импульсов напряжения из более длительных импульсов, имеющих крутой фронт или срез. Они также используются для выполнения математической операции дифференцирования.

Не нашли, что искали? Воспользуйтесь поиском: