
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Электрическая емкость конденсатора.
1. Если электрический заряд каждой из обкладок конденсатора увеличить в n раз, то его электроемкость:
1) увеличится в n раз; 2) уменьшится в n раз; 3) не изменится; 4) увеличится в n² раз.
2. Как изменится электроемкость конденсатора, если электрический заряд на его обкладках уменьшить в n раз при неизменном положении пластин?
1) увеличится в n раз; 2) уменьшится в n раз; 3) не изменится; 4) увеличится в n² раз.
3. Как изменится электрическая емкость плоского конденсатора, если площадь пластин увеличить в 3 раза?
1) не изменится; 2) увеличится в 3 раза; 3) уменьшится в 3 раза; 4) среди ответов 1-3 нет правильного.
4. Электрический заряд на одной пластине конденсатора равен +2 Кл, на другой равен -2 Кл. Напряжение между пластинами равно 5000 В. Чему равна электрическая емкость конденсатора?
1) 0 Ф; 2) 0,0004 Ф; 3) 0,0008 Ф; 4) 2500 Ф.
5. Плоский конденсатор подключен к источнику постоянного тока. Как изменится заряд на пластинах конденсатора, если, не отключая конденсатор от источника, медленно раздвинуть пластины на расстояние, в 2 раза превышающее прежнее?
1) уменьшится в 2 раза; 2) увеличится в 2 раза; 3) не изменится; 4) зависит от скорости раздвижения.
6. Пять конденсаторов соединены параллельно, емкости их равны 1 пФ, 2 пФ, 3 пФ, 4 пФ, 5 пФ. Суммарная емкость составляет:
1) 5 пФ; 2) 15 пФ; 3) 120 пФ; 4) 0,44 пФ.
7. Полное напряжение при последовательном соединении конденсаторов:
1) меньше наименьшего напряжения на отдельных конденсаторах; 2) одинаково на всех конденсаторах; 3) не зависит от емкости конденсаторов; 4) равно сумме напряжений на конденсаторах.
8. Емкость после включения двух конденсаторов последовательно составила 2,22 мкФ. Емкость одного конденсатора 5 мкФ, емкость второго:
1) 7,22 мкФ; 2) 11,1 мкФ; 3) 2,78 мкФ; 4) 4 мкФ.
9. Емкость одного конденсатора в тысячу раз больше другого. При последовательном включении суммарная емкость будет:
1) примерно равной емкости меньшего конденсатора;
2) примерно равной емкости большего конденсатора;
3) примерно равной половине емкости большего конденсатора;
4) значительно выше емкости обоих конденсаторов.
10. Емкость системы из пяти конденсаторов по 1 мкФ практически не изменилась после подключения конденсатора в 1 пкФ. Первоначально конденсаторы были подключены:
1) последовательно; 2) параллельно; 3) в обоих случаях изменение емкости незначительно; 4) в любом случае емкость должна значительно поменяться.
ВОПРОСЫ.
1. Заполните таблицу.
| Величина, закон | Определение величины, формулировка закона | Расчетные формулы |
| Электрический заряд | ||
| Закон сохранения электрического заряда | ||
| Закон Кулона | ||
| Напряженность | ||
| Работа электрического поля | ||
| Потенциал | ||
| Напряжение | ||
| Электроемкость | ||
| Энергия электрического поля |
Электростатика
| Определения величин | Основные законы |
 - напряженность электрического
поля, В/м - напряженность электрического
поля, В/м
 - потенциал, В - потенциал, В
 - разность потенциалов, В - разность потенциалов, В
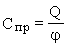 - электроемкость проводника, Ф - электроемкость проводника, Ф
 - электроемкость
конденсатора, Ф - электроемкость
конденсатора, Ф
 - диэлектрическая проницаемость
среды. - диэлектрическая проницаемость
среды. 
| Закон сохранения электрического заряда.
Закон сохранения энергии.
Принцип суперпозиции электрических полей:
 Закон Кулона
Закон Кулона  , Н
Напряженность поля точечного заряда , Н
Напряженность поля точечного заряда  , В/м
Потенциал поля точечного заряда , В/м
Потенциал поля точечного заряда  , В
Связь напряженности и потенциала , В
Связь напряженности и потенциала  , В/м
Электроемкость плоского конденсатора , В/м
Электроемкость плоского конденсатора 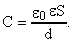 , Ф
Энергия электрического поля, Дж , Ф
Энергия электрического поля, Дж
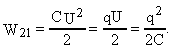
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1 на закон сохранения заряда.
Два одинаковых металлических шарика с зарядами q1=20 нКл и q2=-40 нКл вследствие взаимного притяжения соприкоснулись и снова разошлись на такое же расстояние. Сравнить силы взаимодействия шариков до и после соприкосновения. Изменится ли энергия данной системы зарядов?
F2<F1? Wэл=const?
q1=2010-9 Кл, q2=-4010-9 Кл, r1=r2=r, 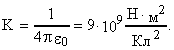
Решение.
В начальном состоянии потенциалы шариков различны, а электроемкости зарядов одинаковы. Из определения электроемкости  получаем
получаем 
Когда шарики соприкасаются, заряды шариков перераспределяются до тех пор, пока потенциалы тел не уравниваются. В условиях равновесия зарядов поверхность проводника представляет собой эквипотенциальную поверхность. Это достигается путем перехода части заряда от тела с более высоким к телу к более низким потенциалом. Заряды тел так же становятся одинаковыми и по модулю и по знаку, q'1=q'2.
Считая систему тел замкнутой, получим по закону сохранения электрического заряда:q1+q2=q'1+q'2.
После соприкосновения заряд распределится поровну между шариками q'1=q'2=(q1+q2)/2=-1010-9Кл.
Силы взаимодействия шариков в начальном и конечном состояниях:
 и
и 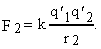
Расстояние r одинаково в обоих состояниях, и k=const, поэтому для ответа на первый вопрос задачи достаточно сравнить произведения зарядов 20(-40)>(-10) (-10), отсюда получаем
F1>F2.
Модуль силы уменьшается, но при этом знак величины сменился на противоположный, то есть притяжение сменилось отталкиванием.
Энергия системы зарядов равна:  где
где  - потенциал электрического поля в том месте, где находится заряд qi.
- потенциал электрического поля в том месте, где находится заряд qi.
В нашем случае: 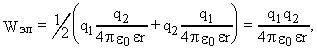
как видим, энергия системы зарядов зависит так же, как сила их взаимодействия, от произведения зарядов. Модуль этого произведения, как уже показано, уменьшается.
Нет ли здесь нарушения закона сохранения энергии? Ответ на этот вопрос несколько выходит за рамки электростатики. Дело в том, что их потенциалы выравниваются, заряды приходят в движение, то есть возникает кратковременный электрический ток. Это приводит к нагреванию проводников и излучению квантов электромагнитной энергии в окружающую среду. В этом смысле наша система из двух заряженных шариков не замкнутая. В то же время алгебраическая сумма зарядов не изменяется, так как заряды не вносятся и не выносятся из системы (кванты не имеют заряда), в этом смысле система замкнута и закон сохранения заряда выполняется.
Пример 2 на закон сохранения заряда
Два плоских воздушных конденсатора равной емкости соединили параллельно, зарядили до 300 В и отключили от источника. Какой станет разность потенциалов на обкладках конденсаторов, если один из них погрузить в керосин?
U'=?; U=300 B, C1=C2=C, e1=e2=1, e'1=1, e'2=39.
Решение.
При параллельном соединении конденсаторов разность потенциалов обкладок у обоих конденсаторов одинакова U=U1=U2. После погружения в диэлектрик второго конденсатора U'=U'1=U'2 напряжение на обоих конденсаторах переменится, но алгебраическая сумма зарядов не постоянна (источник отключен). По закону сохранения электрического заряда
q1+q2=q'1+q'2 (1). Из определения электроемкости конденсатора C=q/U (2), легко получить, что q1=q2, так как C1=C2 и U1=U2 (по условию). Тогда уравнение (1) можно записать в виде 2q=q'1+q'2 или 2CU=CU'+C'2U'. Учитывая, что  , получим
, получим  , e2=39e1 или
, e2=39e1 или  , таким образом
, таким образом  .
.
Ответ: разность потенциалов на обкладках конденсаторов после погружения одного из них в диэлектрик уменьшается и станет равной 15В.
Если конденсаторы не отключать от источника, то напряжение на батарее не изменится и останется равным напряжению источника, т.е. 300В. Заряд же в этом случае не сохраняется, у конденсатора, погружаемого в диэлектрик, он увеличивается пропорционально возрастанию емкости.
Пример 3 на принцип суперпозиции
Определить напряженность и потенциал в точке А электрического поля, созданного двумя точечными зарядами равными 6 нКл каждый, точка А делит пополам расстояние между зарядами.
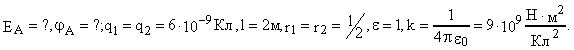
Решение. Для двух положительных зарядов рисунок имеет вид:
Электрическое поле в точке А создается двумя точечными зарядами. Согласно принципу суперпозиции электрических полей напряженность поля в точке А равна геометрической сумме напряженностей  полей, созданных в этой точке зарядами q1 и q2 соответственно:
полей, созданных в этой точке зарядами q1 и q2 соответственно:
 ; проецируя на ось X получим:
; проецируя на ось X получим:  где
где  ,
,  .
.
Если учесть, что  и
и  , получим
, получим  , следовательно,
, следовательно,  .
.
 , так как
, так как 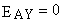 . Таким образом,
. Таким образом,  . Потенциал поля в отличие от напряженности является скалярной величиной. Потенциалы складываются алгебраически:
. Потенциал поля в отличие от напряженности является скалярной величиной. Потенциалы складываются алгебраически:
 , где
, где  и
и  .
.
Из условия задачи следует, что  и
и  . Учитывая, что
. Учитывая, что  , получим
, получим  .
.
Для положительных зарядов  .
.
Если оба заряда q1 и q2 отрицательны  и
и  .
.
Ответ: для одноименных зарядов напряженность электрического поля в точке А равна нулю, а потенциал  .
.
В случае разноименных точечных зарядов рисунок имеет вид:
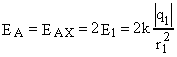 ;
;  . (Докажите самостоятельно).
. (Докажите самостоятельно).
Пример 4 на движение точечного заряда в электрическом поле с применением закона сохранения энергии или теоремы о кинетической энергии.
Какой минимальной кинетической энергий должен обладать протон, чтобы приблизиться к неподвижному протону на расстояние r2=10нм, если r1=10нм?

Первый способ.
Рассмотрим замкнутую систему из двух протонов, так как сила тяжести мала по сравнению с кулоновской силой взаимодействия. В системе отсутствуют силы трения, поэтому сумма потенциальной и кинетической энергий останется постоянной. Таким образом, в силу закона сохранения механической энергии имеем в нашем случае равенство:  ,
,
где EK1 - начальная кинетическая энергия протона B (начальная величина); Ep1 - потенциальная энергия взаимодействия протонов в начальном состоянии; Ek2 = 0, так как, если Ek1 минимальна, то протон B останавливается, приблизившись на расстояние r2 к неподвижному протону A.
Ek1 = Ep1 - Ep2, где
Ep1 = qB j1, Ep2 = qB j2, по определению потенциала.
Потенциал поля точечного заряда qA на расстоянии r равен

По условию задачи r1 >> r2, поэтому начальная потенциальная энергия Ep1 пренебрежимо мала по сравнению с Ep2. Тогда Ek1 = Ep2, или  .
.
Второй способ. Применим для решения задачи теорему о кинетической энергии: работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела  .
.
Пренебрегая силой тяжести протона В и силой гравитационного взаимодействия протонов ввиду малости этих сил по сравнению с кулоновской силой, запишем теорему о кинетической энергии в следующем виде:
 , или
, или  , так как
, так как  по определению разности потенциалов и
по определению разности потенциалов и  по условию.
по условию.
Таким образом, получаем тот же результат:
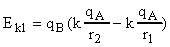 или
или  ;
;
Проверим решение по наименованию единиц:
 .
.
Вычислим значение искомой величины:
 ;
;
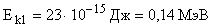 .
.
Такая кинетическая энергия протонов соответствует температуре водорода (протоны - ядра атома водорода), около миллиарда Кельвин. При таких температурах протекают термоядерные реакции (реакции синтеза легких ядер).
Ответ: чтобы сблизиться на расстояние 10-14 м протоны должны обладать энергией около 0,14 МэВ.
Не нашли, что искали? Воспользуйтесь поиском: