
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.
1. Лифт массой 2.4 т равномерно поднимается на высоту 45м за 40с. Определить механическую мощность, развиваемую при подъеме; электрическую мощность, потребляемую двигателем, приводящим в движение лифт; потери мощности в обмотке якоря вследствие нагревания; силу тока и сопротивление обмотки якоря. Напряжение в сети 380 В; КПД 90.
Ответ: N=26.5кВт; Р=29.4кВт; Р=2.9кВт; I=77.4 A; R=0.48 Ом
2. При замыкании источника тока проводником, сопротивление которого 1.8 Ом, в цепи возникает сила тока 0.7 А. Если источник тока замкнуть на сопротивление 2.3 Ом, то сила тока станет равной 0.56 А. Определите силу тока при коротком замыкании.
Ответ: I  = 7 А.
= 7 А.
3. Гальванометр, сопротивление которого 50 Ом, может измерять силу тока до 0.1 А. Как включить его в цепь, чтобы можно было:
1) Измерять силу тока до 10 А?
2) Напряжение до 100 В?
Ответ: R  = 0.505 Ом: R
= 0.505 Ом: R  = 950 Ом.
= 950 Ом.
4. Генератор с напряжением на зажимах 120 В питает цепь из 100 ламп накаливания, соединенных параллельно. Все лампы одинаковые, сопротивлением по 240 Ом. Сопротивление подводящих проводов 0.16 Ом. Найдите общее сопротивление внешней части цепи, силу тока в магистральном проводе, мощность, потребляемую всеми лампами, и ЭДС генератора, если его внутреннее сопротивление 0.16 Ом.
Ответ: R = 2.56 Ом; I = 49.6 А; Р = 5.9 кВт; Е = 135 в.
5. Подъемный кран поднимает груз массой 8.8 т на высоту 10 м в течение 49 сек. Определите силу тока, потребляемого краном, если напряжение 220 В, КПД крана 80%.
Ответ: 100 А.
6. До какой температуры нагревается электромагнит во время работы, если известно, что его обмотка из медного провода при нуле градусов имеет сопротивление 50 Ом, а во время работы оно увеличивается до 58.6 Ом?
Ответ: 40ºС
7. Электровоз ВЛ-60 развивает силу тяги 3.2*10  Н, потребляет ток 1800 А при напряжении 2.5*10
Н, потребляет ток 1800 А при напряжении 2.5*10  В. Определите скорость электровоза, зная, что КПД двигателя 89%. Движение электровоза считать равномерным.
В. Определите скорость электровоза, зная, что КПД двигателя 89%. Движение электровоза считать равномерным.
Ответ: 12.5 м/сек.
8. Какое максимальное усилие развивает дизельный электротрактор ДЭТ—250 при скорости передвижения 0.56 м/сек если его тяговый электродвигатель, имеющий КПД 72%, работает при токе 360 А и напряжении 470 В? Ответ: 2.2*10  Н.
Н.
9. На зажимах дуги сварочной машины поддерживается напряжение 20 В. Сила тока, питающего дугу, 200 А, время работы - 7 часов. Какова стоимость расхода электроэнергии электросварочным аппаратом, если 3.6*10 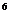 Дж энергии стоят 160 руб?
Дж энергии стоят 160 руб?
Ответ: 4500 руб.
10. К батарее через реостат подключен вольтметр. Если сопротивление резистора уменьшить в три раза по сравнению с первоначальным значением, то показания вольтметра возрастут в два раза. Во сколько раз изменятся показания вольтметра, если сопротивление реостата уменьшить до нуля?
Ответ: увеличится в 4 раза.
11. Когда сопротивление внешней части источника тока уменьшили на 30%, то ток увеличился на 30%. На сколько процентов увеличится ток, если сопротивление внешней части цепи уменьшится на 50°/.
Ответ: 62.5%
12. Аккумулятор заряжается током 4А. Какое дополнительное сопротивление следует ввести в цепь, если остаточная ЭДС аккумулятора 9В, его внутреннее сопротивление 1 Ом, а зарядка осуществляется от источника постоянного напряжения 21 В.
Ответ: 2 Ом.
13. Вольтметр, подключенный к аккумулятору с внутренним сопротивлением 1 Ом. показывает 1.2 В. Если последовательно с ним включено сопротивление 20 Ом, вольтметр показывает 1 В. Определить сопротивление вольтметра.
Ответ: 99 Ом.
14. Амперметр для измерения тока до 2А с внутренним сопротивление 0.1 Ом необходимо использовать для измерения токов до 22А. Какое сопротивление должен иметь шунт?
Ответ: 0.01 Ом.
15. Два проводника соединены параллельно R 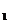 =10 Ом и R
=10 Ом и R 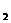 =16 Ом. При прохождении тока на первом проводнике выделяется количество теплоты, равное 40Дж. Определить, какое количество теплоты выделится в обоих проводниках при их последовательном соединении за то же время.
=16 Ом. При прохождении тока на первом проводнике выделяется количество теплоты, равное 40Дж. Определить, какое количество теплоты выделится в обоих проводниках при их последовательном соединении за то же время.
Ответ: 15.4Дж.
16. Требуется передать мощность 100кВт на расстояние 67.5 км, чтобы потери на нагревание не превышали 3% передаваемой энергии. Какова масса проводов, если ток передается под напряжением 6кВ, плотность материала провода 8.8*10кг/м³, его удельное сопротивление 1.7*10  Ом*м.
Ом*м.
Ответ: 28*10³ кг.
17. Чтобы получить 0,5л кислорода при температуре 57 С, через слабый раствор серной кислоты в течение 60 мин пропускали электрический ток. Определите массу полученного кислорода и его давление, если электролиз протекал при силе тока 2.6 А.
Ответ: m = 0.78 г; Р = 133 кПа.
18. В электролитической медной ванне за 40 мин выделилось 1.93*10  кг меди. Определите ЭДС батареи, необходимой для питания током ванны, если сопротивление раствора 1.3 Ом, внутреннее сопротивление батареи 0.3 Ом.
кг меди. Определите ЭДС батареи, необходимой для питания током ванны, если сопротивление раствора 1.3 Ом, внутреннее сопротивление батареи 0.3 Ом.
Ответ: 4 В.
19. При серебрении пластинки через раствор электролита проходит так плотностью j=0,6 А/см². С какой средней скоростью растет толщина серебряного слоя, если плотность серебра 10.5*10³ кг/м³, а его электрохимический эквивалент 1.118*10  кг/Кл?
кг/Кл?
Ответ: 7.5*10  м/с
м/с
20. При никелировании изделия в течение 1ч отложился слой никеля толщиной l=0.01 мм. Определить плотность тока, если атомная масса никеля А=0.0587 кг/моль, валентность n=2, плотность никеля р=8.8*10³ кг/м³.
Ответ: 81.3 A/м³.
21. Определить количество выделившегося на катоде при электролизе алюминия (Al 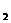 SO
SO  ), если затрачено 20кВт-ч энергии при напряжении на электродах 12 В, КПД установки 80%. Электрохимический эквивалент алюминия k = 9.3*10
), если затрачено 20кВт-ч энергии при напряжении на электродах 12 В, КПД установки 80%. Электрохимический эквивалент алюминия k = 9.3*10  кг/Кл.
кг/Кл.
Ответ: m =0.45кг.
МАГНИТНОЕ ПОЛЕ
Открытие магнитного поля. Постоянные магниты и магнитное поле Земли. Магнитная индукция Магнитная постоянная. Магнитная проницаемость среды. Графическое изображение магнитных полей. Напряженность магнитного поля. Взаимодействие токов. Магнитные поля проводника с током и соленоида. Действие магнитного поля на проводник с током. Закон Ампера. Магнитный поток. Действие магнитного поля на движущийся заряд. Сила Лоренца. Определение удельного заряда. Магнитосфера Земли и ее взаимодействие с солнечным ветром. Движение заряженной частицы в магнитных и электрических полях. Радиационные пояса Земли. Магнитные свойства вещества. Кривая намагничивания.
Магнитное взаимодействие токов window.top.document.title = "1.16. Магнитное взаимодействие токов";
Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. Он появился в Европе приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.
Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда (1820 г.). Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.
По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.
Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).
Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако, опыт показывает, что изолированных магнитных зарядов не существует.
Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности  электрического поля. Такой характеристикой является вектор магнитной индукции
электрического поля. Такой характеристикой является вектор магнитной индукции  Вектор магнитной индукции
Вектор магнитной индукции  определяет силы, действующие на токи или движущиеся заряды в магнитном поле.
определяет силы, действующие на токи или движущиеся заряды в магнитном поле.
За положительное направление вектора  принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора
принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора  Такое исследование позволяет представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор
Такое исследование позволяет представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор  направлен по касательнойОбратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
направлен по касательнойОбратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора  но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
| F ~ IΔl sin α. |
Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора  определяется следующим образом:
определяется следующим образом:
Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δ l:
|
В общем случае сила Ампера выражается соотношением:
|
Это соотношение принято называть законом Ампера.
В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).

|
Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.
Сила Ампера направлена перпендикулярно вектору магнитной индукции  и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции
и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции  входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).
входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).

|
| Правило левой руки и правило буравчика. |
Если угол α между направлениями вектора  и тока в проводнике отличен от 90°, то для определения направления силы Ампера
и тока в проводнике отличен от 90°, то для определения направления силы Ампера  более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор
более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор  и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора
и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора  Поступательное перемещение буравчика будет показывать направление силы Ампера
Поступательное перемещение буравчика будет показывать направление силы Ампера  (рис. 1.16.2). Правило буравчика часто называют правилом правого винта.
(рис. 1.16.2). Правило буравчика часто называют правилом правого винта.
Одним из важных примеров магнитного взаимодействия токов является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.
Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.
Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

|
В Международной системе единиц СИ коэффициент пропорциональности k принято записывать в виде:
| k = μ0 / 2π, |
где μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно
| μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2. |
Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид:
|
Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы  и
и  магнитной индукции параллельных токов I1 и I2 лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, нужно в законе Ампера положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
магнитной индукции параллельных токов I1 и I2 лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, нужно в законе Ампера положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
|
Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора  магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора
магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора  если при вращении буравчик перемещается в направлении тока (рис.).
если при вращении буравчик перемещается в направлении тока (рис.).

|
| Магнитное поле прямолинейного проводника с током. |

|
| Магнитное взаимодействие параллельных и антипараллельных токов. |
поясняет закон взаимодействия параллельных токов.
Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:
Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10–7 H на каждый метр длины.
Магнитное поле
Магнитное поле в веществе window.top.document.title = "1.19. Магнитное поле в веществе";
Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.
Физическая величина, показывающая, во сколько раз индукция  магнитного поля в однородной среде отличается по модулю от индукции
магнитного поля в однородной среде отличается по модулю от индукции  магнитного поля в вакууме, называется магнитной проницаемостью:
магнитного поля в вакууме, называется магнитной проницаемостью:
|
Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.
Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.
Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10–5, у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10–6), вода (μ – 1 ≈ –9·10–6), висмут (μ – 1 ≈ –1,7·10–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис.).

|
| Рисунок. Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле. |
Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против индукции внешнего поля.
В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.
Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако, во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем (1845 г.).
Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 102–105. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.
К группе ферромагнетиков относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.
Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.
Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.
Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).
Магнито-жесткие материалы сохраняют в значительной мере свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовления постоянных магнитов.
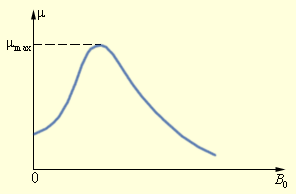
Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B0 внешнего поля. Типичная зависимость μ (B0) приведена на рис. 1 В таблицах обычно приводятся значения максимальной магнитной проницаемости.
|
| Рисунок 1. Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля. |
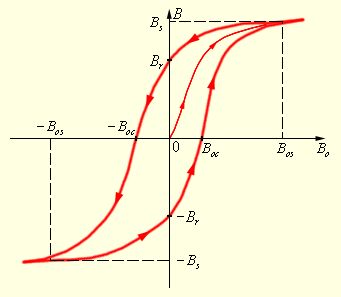
Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции B магнитного поля в ферромагнетике от индукции B0 внешнего магнитного поля. Характерной особенностью процесса намагничивания ферромагнетиков является так называетмый гистерезис, то есть зависимость намагничивания от предыстории образца. Кривая намагничивания B (B0) ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 2.).
|
| Рисунок 2 Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции B0 внешнего магнитного поля. |
Из рис. 1.19.3 видно, что при  наступает магнитное насыщение – намагниченность образца достигает максимального значения.
наступает магнитное насыщение – намагниченность образца достигает максимального значения.
Если теперь уменьшать магнитную индукцию B0 внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно Br. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию B0 до значения –B0c, которое принято называть коэрцитивной силой. Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. У магнито-мягких материалов значения коэрцитивной силы B0c невелико – петля гистерезиса таких материалов достаточно «узкая». Материалы с большим значением коэрцитивной силы, то есть имеющие «широкую» петлю гистерезиса, относятся к магнито-жестким.
Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка 10–2–10–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.
В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем окажется ненамагниченным. При наложении внешнего магнитного поля  происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение. Рис. может служить качественной иллюстрацией процесса намагничивания ферромагнитного образца.
происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение. Рис. может служить качественной иллюстрацией процесса намагничивания ферромагнитного образца.

|
| Рисунок. Намагничивание ферромагнитного образца. (1) B0 = 0; (2) B0 = B01; (3) B0 = B02 > B01. |
Электромагнитная индукция. Правило Ленца. window.top.document.title = "1.20. Электромагнитная индукция. Правило Ленца";
Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
Магнитным потоком Φ через площадь S контура называют величину
|
где B – модуль вектора магнитной индукции, α – угол между вектором  и нормалью
и нормалью  к плоскости контура (рис.).
к плоскости контура (рис.).

|
Рисунок
Магнитный поток через замкнутый контур. Направление нормали  и выбранное положительное направление и выбранное положительное направление 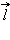 обхода контура связаны правилом правого буравчика. обхода контура связаны правилом правого буравчика.
|
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
| 1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции Eинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
|
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение называется правилом Ленца (1833 г.).
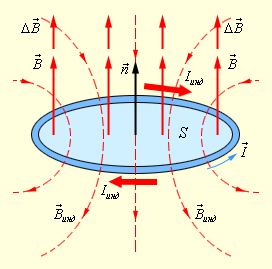
Рис. иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
|
Рисунок
Иллюстрация правила Ленца. В этом примере  а а  инд < 0. Индукционный ток Iинд течет навстречу выбранному положительному направлению инд < 0. Индукционный ток Iинд течет навстречу выбранному положительному направлению 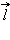 обхода контура. обхода контура.
|
Правило Ленца отражает тот экспериментальный факт, что  инд и
инд и 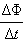 всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле  перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью
перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью  по двум другим сторонам (рис.).
по двум другим сторонам (рис.).
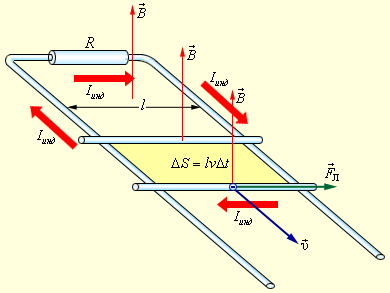
|
| Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон. |
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью  зарядов, направлена вдоль проводника. Эта составляющая указана на рис. Она играет роль сторонней силы. Ее модуль равен
зарядов, направлена вдоль проводника. Эта составляющая указана на рис. Она играет роль сторонней силы. Ее модуль равен
| FЛ = eυB |
Работа силы FЛ на пути l равна
| A = FЛ · l = eυBl. |
По определению ЭДС
|
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для  инд можно придать привычный вид. За времы Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
инд можно придать привычный вид. За времы Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,

|
Для того, чтобы установить знак в формуле, связывающей  инд и
инд и 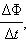 нужно выбрать согласованные между собой по правилу правого буравчика направление нормали
нужно выбрать согласованные между собой по правилу правого буравчика направление нормали  и положительное направление обхода контура
и положительное направление обхода контура  как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный Iинд =  инд/R. За время Δt на сопротивлении R выделится джоулево тепло
инд/R. За время Δt на сопротивлении R выделится джоулево тепло

|
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера  . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = IBl. Сила Ампера направлена навстречу движения проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
. Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = IBl. Сила Ампера направлена навстречу движения проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна

|
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом (1861 г.).
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Сила Лоренца - это магнитная сила, действующая на движущийся заряд в магнитном поле, источником которого являются другие движущиеся заряды:
Fл = QvB sina,
Q - заряд частицы, v - ее скорость, В - магнитная индукция, a - угол между векторами v и В. Если v перпендикулярна В, то сила Лоренца имеет максимальное значение:
Fлм = QvB;
Если v параллельна В, то сила равна нулю.
На плоский контур тока малых размеров, помещенный в магнитное поле, действует механический момент сил
M = ISB sina,
I - сила тока, S - площадь контура, В - магнитная индукция, a - угол между нормалью к плоскости контура и вектором В.
Векторная величина
pм = IS n ,
где n - единичный вектор нормали, называется магнитным моментом контура; модуль магнитного момента
pм = IS.
Направление магнитного момента определяется по правилу правого винта: если вращать по направлению тока в контуре, то его поступательное перемещение будет совпадать с направлением pм и единичным вектором нормали n. Если n перпендикулярен В, то момент сил имеет максимальное значение
Мм = ISB.
Определения магнитной индукции:
a) вектор, модуль которого равен максимальной силе, действующей на движущийся со скоростью 1 м/с точечный заряд 1 Кл:
B = Fлм / (Qn).
Направление В определяется по правилу левой руки.
б) вектор, модуль которого равен максимальному механическому моменту, действующему на плоский контур тока с единичным магнитным моментом:
B = Fм / (I∆l).
Направление В определяется по правилу левой руки.
в) вектор, модуль которого равен максимальному механическому моменту, действующему на плоский контур тока с единичным магнитным моментом:
B = Мм / (IS).
Направление В определяется по правилу правого винта.
 |
Закон Био-Савара-Лапласа: линейный элемент тока является источником магнитного
поля, магнитная индукция которого во внешнем пространстве
Напряженность магнитного поля в вакууме – векторная величина
H = B / m0.
Напряженность магнитного поля в среде
Hc = B / (m0m).
m - относительная магнитная проницаемость среды.
Взаимодействие двух параллельных проводников с токами обусловлено магнитными силами, которые действуют между движущимися носителями зарядов в проводниках; кулоновское взаимодействие в этом случае равно нулю, так как проводники электрически нейтральны (взаимодействие между носителями зарядов на поверхности проводника не учитывается). Два длинных прямолинейных и параллельных проводника притягиваются друг к другу, если токи имеют одинаковое направление; если токи имеют противоположные направления, то проводники отталкиваются. Модуль магнитной силы
 |
a – расстояние между параллельными проводниками, I1 и I2 – силы тока в них, l - их длина, m0 - магнитная постоянная (m0 = 4p*10-7 Гн/м),
m - относительная магнитная проницаемость среды. m0p
Не нашли, что искали? Воспользуйтесь поиском:





