
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Распределение инвестиций по строительным проектам при несравнимых критериях (медиана Кемени)
В процессе функционирования каждой фирме приходится решать трудную задачу определения размера и сферы приложения инвестиций. Как и любым управленческим решениям, подобным решениям сопутствует риск, определяемый как вероятность определенного уровня потерь. Одним из возможных способов уменьшения риска предпринимательской деятельности является диверсификация производства или создание инвестиционного портфеля, т.е. вложение капитала в различные виды ценных бумаг или компании, работающие в разных областях. Например, строительная организация может распределять имеющиеся средства между следующими направлениями: строительство жилья, торговая деятельность строительными материалами, производство изделий на собственной базе, реконструкция и капитальный ремонт, программы переселения.
В условиях рыночной экономики любое предприятие стремится диверсифицировать собственную деятельность: производитель набирает портфель различных видов деятельности, решая дилемму риск - доходность.
Управляющему необходимо распределить ресурсы между некоторым конечным числом направлений, при чем в каждое из них должна быть вложена хоть какая-то сумма средств (отличная от нуля). Пронумеруем все программы деятельности, пусть i – порядковый номер направления ( ). Затем формируется множество критериев, по которым будет оцениваться эффективность каждого направления деятельности (в качестве критериев, которые предприятию необходимо максимизировать или минимизировать, например, могут быть рассмотрены различные характеристики: качество выполнения работы, средняя заработная плата, скорость выполнения, загрязнение окружающей среды, которое будет произведено в ходе выполнения программы). Производится сбор исходных данных по каждой из рассматриваемых программ инвестирования. Положим всего имеется m оцениваемых параметров. Каждый j-ый частный критерий дает свой вектор предпочтений
). Затем формируется множество критериев, по которым будет оцениваться эффективность каждого направления деятельности (в качестве критериев, которые предприятию необходимо максимизировать или минимизировать, например, могут быть рассмотрены различные характеристики: качество выполнения работы, средняя заработная плата, скорость выполнения, загрязнение окружающей среды, которое будет произведено в ходе выполнения программы). Производится сбор исходных данных по каждой из рассматриваемых программ инвестирования. Положим всего имеется m оцениваемых параметров. Каждый j-ый частный критерий дает свой вектор предпочтений 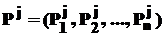 ,
,  , где
, где  - порядковый номер проекта, занимающего в ранжировании по j-му критерию i-ое место. В каждом ранжировании первое место занимает наиболее привлекательное, с точки зрения рассматриваемого критерия, для предприятия направление деятельности и далее по убыванию. Или же могут быть приглашены m независимых экспертов, каждый из которых сформирует свой вектор предпочтений. Затем каждому вектору
- порядковый номер проекта, занимающего в ранжировании по j-му критерию i-ое место. В каждом ранжировании первое место занимает наиболее привлекательное, с точки зрения рассматриваемого критерия, для предприятия направление деятельности и далее по убыванию. Или же могут быть приглашены m независимых экспертов, каждый из которых сформирует свой вектор предпочтений. Затем каждому вектору  поставим в соответствие вектор
поставим в соответствие вектор  , сформированный по правилу: координата
, сформированный по правилу: координата  – число направлений, которые согласно j-му частному критерию являются более предпочтительными, чем направление имеющее порядковый номер i.
– число направлений, которые согласно j-му частному критерию являются более предпочтительными, чем направление имеющее порядковый номер i.
Следующим шагом является поиск группового ранжирования, в котором наилучшим образом будут представлены индивидуальные предпочтения. В качестве такового рассматривается медиана Кемени, определяемая следующим образом:

где  – расстояние между двумя ранжированиями, определяемое по формуле
– расстояние между двумя ранжированиями, определяемое по формуле
 .
.
Для отыскания медианы Кемени, во-первых, строим матрицу потерь  , для чего рассматриваем векторы
, для чего рассматриваем векторы  , в которых направление с номером k (
, в которых направление с номером k (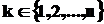 ) расположено на l-ом месте, где l последовательно изменяется от 1 до n (т.е.
) расположено на l-ом месте, где l последовательно изменяется от 1 до n (т.е.  ), тогда
), тогда
 (1.6..1)
(1.6..1)
Отыскание медианы Кемени эквивалентно решению задачи о назначениях, коэффициенты целевой функции которой определяются формулой (1.6.1), а сама задача записывается следующим образом:
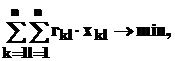 (1.6.2)
(1.6.2)
 (1.6.3)
(1.6.3)
 (1.6.4)
(1.6.4)
 (1.6.5)
(1.6.5)
В результате получаем матрицу  , по которой восстанавливаем вектор группового предпочтения P*:
, по которой восстанавливаем вектор группового предпочтения P*:
· анализируем матрицу X* по строкам: если  , то в векторе P* полагаем
, то в векторе P* полагаем  ;
;
· по упорядочению P* составляем матрицу парных сравнений  ,
,  для группового предпочтения, элементы которой определяются:
для группового предпочтения, элементы которой определяются:  , если согласно ранжированию P* направление, имеющее порядковый номер k, является более предпочтительным, чем l-ое направление;
, если согласно ранжированию P* направление, имеющее порядковый номер k, является более предпочтительным, чем l-ое направление;  , если k-ый и l-ый виды деятельности равнопредпочтительны; и
, если k-ый и l-ый виды деятельности равнопредпочтительны; и  , если k-ый менее предпочтителен, чем l-ый;
, если k-ый менее предпочтителен, чем l-ый;
· считаем сумму элементов каждой строки и сумму всех элементов матрицы:
 ;
;
· находим доли, соответствующие каждому направлению деятельности:

Распределить средства между 4 направлениями, имеющими характеристики указанные в табл. 1.6.1.
Таблица 1.6.1
| Характеристики | Направления | |||
| I | II | III | IV | |
| Планируемая прибыль | ||||
| Оценка риска | 0.3 | 0.2 | 0.4 | 0.8 |
| Средняя заработная плата | ||||
| Период окупаемости | ||||
| Энергоемкость | 0.81 | 0.37 | 0.63 | 0.66 |
В качестве критериев рассматривать приведенные характеристики.
1. Согласно каждому критерию построен вектор предпочтения P j и соответствующий ему вектор π j:
критерий «прибыль» - P1=(4, 2, 3, 1), π1 =(3, 1, 2, 0);
критерий «риск» - P2=(2, 1, 3, 4), π2 =(1, 0, 2, 3);
критерий «заработная плата» - P3=(3, 4, 2, 1), π3 =(3, 2, 0, 1);
критерий «период окупаемости» - P4=(4, 3, 2, 1), π4 =(3, 2, 1, 0);
критерий «энергоемкость» - P5=(2, 3, 4, 1), π5 =(3, 0, 1, 2).
2. Найдены элементы матрицы потерь R={rkl}, определяемые по (4.2):
r11=|π1 - π 11|+|π1 - π 21|+|π1 - π 31|+|π1 - π 41|+|π1 - π 51|=|0-3|+|0-1|+|0-3|+|0-3|+|0-3|= =13, где π1=0 {первая альтернатива в векторе π занимает первое место};
r12=|π1 - π 11|+|π1 - π 21|+|π1 - π 31|+|π1 - π 41|+|π1 - π 51|=|1-3|+|1-1|+|1-3|+|1-3|+|1-3| =8, где π1 =1 {первая альтернатива в векторе π занимает второе место};
r13=|π1 - π 11|+|π1 - π 21|+|π1 - π 31|+|π1 - π 41|+|π1 - π 51|=|2-3|+|2-1|+|2-3|+|2-3|+|2-3| =5, где π1 =2 {первая альтернатива в векторе π занимает третье место};
r14=|3-3|+|3-1|+|3-3|+|3-3|+|3-3|=2, где π1=3 {первая альтернатива в векторе π занимает четвертое место};
r21=|π2 - π 12|+|π2 - π 22|+|π2 - π 32|+|π2 - π 42|+|π2 - π 52|=|0-1|+|0-0|+|0-2|+|0-2|+|0-0| =5, где π2 =0 {вторая альтернатива в векторе π занимает первое место};
r22=|1-1|+|1-0|+|1-2|+|1-2|+|1-0|=4; r23=|2-1|+|2-0|+|2-2|+|2-2|+|2-0| =5;
r24=|3-1|+|3-0|+|3-2|+|3-2|+|3-2| =5;
r31=6; r32=3; r33=4; r34=9; r41=6; r42=5; r43=6; r44=9.
3. Решена задача о назначениях, целевая функция которой представлена матрицей:

Для решения задачи о назначениях применим венгерский метод, который состоит в следующем:
0-ая итерация (“приведение исходной матрицы”). В каждой строке ищется минимальный элемент  , который затем вычитается из каждой строки матрицы, т.о. обеспечивается в каждой строке наличие хотя бы одного нуля. В преобразованной матрице
, который затем вычитается из каждой строки матрицы, т.о. обеспечивается в каждой строке наличие хотя бы одного нуля. В преобразованной матрице 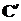 находим минимальный элемент в каждом столбце
находим минимальный элемент в каждом столбце  , вычитаем его из каждого столбца.
, вычитаем его из каждого столбца.
k-ая итерация ( , “подсчет числа независимых нулей”). Определяется минимальное число линий, которыми можно вычеркнуть все нули в матрице. Если число таких линий n, то в матрице n независимых нулей, и по преобразованной матрице
, “подсчет числа независимых нулей”). Определяется минимальное число линий, которыми можно вычеркнуть все нули в матрице. Если число таких линий n, то в матрице n независимых нулей, и по преобразованной матрице  выписываем результат: в матрице
выписываем результат: в матрице 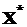 на месте нулевых элементов матрицы
на месте нулевых элементов матрицы  стоят единицы, а на месте ненулевых элементов - нули. Если этих линий меньше n, то переходим к k+1- ой итерации.
стоят единицы, а на месте ненулевых элементов - нули. Если этих линий меньше n, то переходим к k+1- ой итерации.
k+1-ая итерация. Среди всех незачеркнутых элементов матрицы ищем  . Обозначим незачеркнутые элементы
. Обозначим незачеркнутые элементы  , зачеркнутые один раз
, зачеркнутые один раз  , зачеркнутые дважды -
, зачеркнутые дважды -  . Осуществим преобразование матрицы
. Осуществим преобразование матрицы

и переходим к k -му этапу.
Рассмотрим пример. Есть 5 работ и 5 исполнителей; матрица затрат
 ,
,
где  – затраты, если на i -ую работу назначается исполнитель j -го типа. Распределить исполнителей по работам таким образом, чтобы суммарные затраты были минимальными.
– затраты, если на i -ую работу назначается исполнитель j -го типа. Распределить исполнителей по работам таким образом, чтобы суммарные затраты были минимальными.
0-я итерация ( приведение матрицы):
 »
» 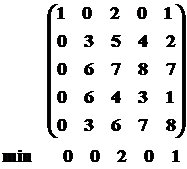 »
» 
1-я итерация (подсчет числа независимых нулей):


Число независимых нулей равно 3.
2-я итерация  . Преобразуем матрицу по формуле (3.9) при
. Преобразуем матрицу по формуле (3.9) при  :
:

3-я итерация Находим минимальное число линий, которыми можно перечеркнуть все нули в матрице  (число независимых нулей):
(число независимых нулей):


4-я итерация  . После преобразования матрицы по формуле (3.9) при
. После преобразования матрицы по формуле (3.9) при  получаем:
получаем:

5-я итерация Число независимых нулей в матрице  равно 5, т.к. все нули можно перечеркнуть, используя только пять линий:
равно 5, т.к. все нули можно перечеркнуть, используя только пять линий:


На следующем рисунке выделены независимые нули:


Соответствующая матрица «назначений» имеет вид:
 ,
,
т.е. для того, чтобы получить минимальные затраты Ф*=с14 + с25 + с31 + с43+ +с52=1+5+2+8+5=11, необходимо назначить 1 -го исполнителя на 4 -ый вид работ; 2 -го исполнителя – на 5 -ый; 3 -го исполнителя - на 1 -ый; 4 -ый - на 3 -ий; 5 -ый - на 2 -ой вид работ.
Применим этом алгоритм для решения полученной задачи. В этом случае решением будет является матрица X:

4. Матрице X соответствует вектор группового предпочтения P*= (2, 3, 4, 1).
5. Вектору P* соответствует матрица предпочтений L:

6. Все средства могут быть вложены в «лучшее» направление – второе, или же предлагается распределение, соответствующее матрице предпочтений L.
7. Сумма строк матрицы:  ,
,  ,
, 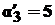 ,
,  . Сумма всех элементов матрицы составила
. Сумма всех элементов матрицы составила  . Доли, соответствующие каждому направлению деятельности: χ1 = ά1/ά = 1/16 = 0,0625, χ2 = ά2/ά = 7/16 = 0,4375, χ3 = ά3/ά = = 5/16 = 0,3125, χ4 = ά4/ ά = 3/16 = 0,1875.
. Доли, соответствующие каждому направлению деятельности: χ1 = ά1/ά = 1/16 = 0,0625, χ2 = ά2/ά = 7/16 = 0,4375, χ3 = ά3/ά = = 5/16 = 0,3125, χ4 = ά4/ ά = 3/16 = 0,1875.
Не нашли, что искали? Воспользуйтесь поиском: