
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Моделирование эпидемии
Практическая работа
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных 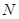 изменяется по формуле
изменяется по формуле
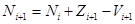 ,
,
где 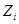 – количество заболевших в
– количество заболевших в 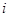 -й день, а
-й день, а 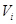 – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
– количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
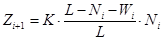 ,
,
где 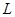 – общая численность жителей,
– общая численность жителей, 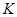 – коэффициент роста и
– коэффициент роста и  – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
– число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
 .
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при 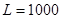 и
и 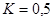 до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
Ответьте на следующие вопросы:
1. Когда закончится эпидемия?
Ответ:
2. Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
3. Каково максимальное число больных в один день?
Ответ:
4. Изменяя коэффициент 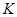 , определите, при каких значениях
, определите, при каких значениях 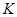 модель явно перестает быть адекватной.
модель явно перестает быть адекватной.
Ответ:
5. *Сравните модель, использованную в этой работе, со следующей моделью:
 ,
,  .
.
Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Ответ:
Сравните поведение двух моделей при 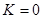 ,
,  и
и 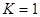 . Сделайте выводы.
. Сделайте выводы.
Ответ:
После выполнения задание можно отправить на эл почту natalischool2@mail.ru
Желаю удачи!
| <== предыдущая лекция | | | следующая лекция ==> |
| | |
Не нашли, что искали? Воспользуйтесь поиском: