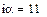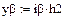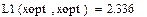От объёма товара от объёма товара

В этих условиях прибыль каждой фирмы определиться следующими функциями:

L₁(x,y) = xf (x + y) – φ(x), L₂(x,y) = yf (x + y) – φ(y).

Рассмотрим вариант поведения конкурентов с точки зрения теории игр.

Пусть будет игра с нулевой суммой с выигрышем первого игрока

L₁(x,y) = xf (x + y) – φ(x),

цель второго игрока – минимизировать прибыль первой фирмы для её разорения, то есть необходимо найти

max min L(x,y) =max min (xf (x + y) – φ(x)).

^{x y x y}

Сведём игру к матричной игре, представив стратегии обоих игроков в дискретном виде x_i = ih₁, y_j = jh₂, i,j = 1,2,…,N. Решение для первого игрока приведено ниже:

Вывод: в соответствии с этим решением второй игрок должен поддерживать максимальный объём продаж с целью снизить цены минимизировать прибыль первого игрока. Первый игрок находит оптимальный объём производства в этих условиях, однако получает меньшую прибыль, чем второй игрок.

Если конкуренты смогут достичь соглашения о разделе рынка, то они могут достичь наиболее выгодного для каждого из них результата с прибылью 2,336 единиц, как показано ниже [1]:

Не нашли, что искали? Воспользуйтесь поиском: