Задачи для самостоятельного решения. на пересечении которых он находится.

3.1. Дана матрица A(N, M). Найдите её наибольший элемент и номера строки и столбца,

на пересечении которых он находится.

3.2. В каждой строке заданной матрицы A(N, M) вычислите сумму, количество и среднее

арифметическое положительных элементов.

3.3. Для заданной целочисленной матрицы A(N, M) определите, является ли сумма её элементов чётным числом, и выведите на печать соответствующий текст.

3.4. Дана матрица A(N, M). Найдите количество элементов этой матрицы, больших среднего арифметического всех её элементов.

3.5. Дана целочисленная матрица A(N, M). Вычислите сумму и произведение тех её элементов, которые при делении на два дают нечётное число.

3.6. В заданной матрице A(N, M) поменяйте местами столбцы с номерами P и Q.

3.7. Дана матрица A(N, M). Вычислите вектор X(M), где значение Xj равно сумме положительных элементов j -го столбца матрицы A.

3.8. Дана матрица A(N, M). Получите вектор X(M), равный P -й строке матрицы, и вектор

Y(N), равный Q -му столбцу матрицы.

3.9. Дана матрица A(N, M). Поменяйте местами её наибольший и наименьший элементы.

3.10. По заданному n постройте матрицы размером (n,n) вида

а) 1 0... 0 б) n n-1 n-2... 1 в) 0 0... 0 1

0 1... 0 0 n n-1... 2 0 0... 1 2

..............

0 0... 1 0 0 0... n 1 2... n-1 n

3.11. Даны две целочисленные матрицы A(N, M) и B(N, M). Подсчитате (в отдельности)

количество тех пар (ai j, bi j), для которых:

а) ai j < bi j;

б) ai j = bi j;

в) ai j > bi j.

3.12. Дана матрица A(N, N). Перепишите элементы её главной диагонали в одномерный

массив Y(N) и разделите их на максимальный элемент главной диагонали.

3.13. Дана матрица A(N, M). Получите Y = X1. XN + X2. XN-1 +... + XN. X1, где Xi -наибольший элемент в строке с номером i матрицы A.

3.14. Постройте матрицу A(N, N), элементы которой определяются равенствами ai j = i + 2. j, а также найдите произведение чётных элементов этой матрицы, удовлетворяющих условию ai j < P (0 < P < 3N).

3.15. Найдите наибольший элемент побочной диагонали заданной матрицы A(N, N) и

выведите на печать всю строку, в которой он находится.

3.16. Дана целочисленная матрица A(N, M). Вычислите сумму и произведение нечётных

отрицательных элементов матрицы, удовлетворяющих условию | ai j | < i.

3.17. Для заданной матрицы А(N, N) найдите:

а) сумму всех элементов;

б) сумму элементов главной диагонали;

в) значения наибольшего и наименьшего из элементов главной диагонали.

3.18. По трём заданным матрицам А(N, N), В(N, N) и С(N, N) постройте матрицу Х того

же размера, каждый элемент которой вычисляется по формуле xi j = max { ai j, bi j, ci j }.

3.19. Дана матрица А(N, N) и целое P. Преобразуйте матрицу по правилу: строку с номером P сделайте столбцом с номером P, а столбец с номером P сделайте строкой с номером P.

3.20. Для заданной матрицы A(N, N) найдите сумму элементов, расположенных в строках

с отрицательным элементом на главной диагонали.

3.21. Дана матрица A(N, M). Определите:

а) число ненулевых элементов в каждой строке матрицы;

б) общее число ненулевых элементов в матрице;

в) отношение числа ненулевых элементов в каждой строке матрицы к общему числу

ненулевых элементов в матрице.

3.22. Вычислите матрицу С(N, N), являющуюся суммой матриц А(N, N) и В(N, N).

Матрица А задана, а элементы матрицы B вычисляются по формуле

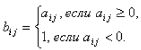
3.23. Из заданной матрицы A(N, M) удалите строку с номером K и столбцы с номерами P

и Q. Полученную матрицу уплотните.

3.24. В заданном массиве X(N, M) все числа различны. В каждой строке выбирается минимальный элемент, затем среди этих чисел выбирается максимальное. Напечатайт номер строки массива Х, в которой расположено выбранное число.

3.25. В заданном массиве A(N, M) переставьте строки так, чтобы суммы их элементов возрастали.

3.26. В заданном массиве A(N, N) вычислите две суммы элементов, расположенных выше

и ниже побочной диагонали.

3.27. Дана матрица A(N, M). Переставляя её строки и столбцы, добейтесь того, чтобы наибольший элемент (один из них) оказался в верхнем левом углу.

3.28. Расстояние между двумя множествами точек — это расстояние между наиболее

близко расположенными точками этих множеств. Найдите расстояние между двумя заданными множествами точек на плоскости.

3.29. В заданном множестве точек на плоскости найдите пару точек с максимальным расстоянием между ними.

3.30. Задан список участников соревнований по плаванию и их результаты. Расположите

результаты и фамилии участников в соответствии с занятым местом.

3.31. На основе сведений о ежедневном пробеге на тренировке спортсменов команды

рассчитате среднесуточный и общий пробег каждого спортсмена за 20 дней.

3.32. Известен расход по N видам горючего в каждом из M автохозяйств. Определите для

каждого хозяйства вид горючего с наибольшим и с наименьшим расходом.

3.33. На основе сведений об отметках учеников класса в последней четверти

а) вычислите средние баллы по каждому предмету;

б) определите группу из пяти лучших учеников;

в) определите группу из пяти самых слабых учеников.

3.34. Заданы запасы по N видам топлива в каждом из М районов города и нормы минимально допустимого запаса по каждому виду топлива. Определите:

а) запасы каждого вида топлива на все районы;

б) запасы всех видов топлива для каждого района;

в) в каких районах запас того или иного вида топлива меньше минимально допустимого

и каких видов топлива запасено недостаточно в каждом районе.

3.35. Последовательно (в лексикографическом порядке) напечатайте всевозможные перестановки целых чисел 1, 2,..., n. Значение n задано.

3.36*. Напечатать элементы заданной матрицы А(N, N) в следующем порядке:

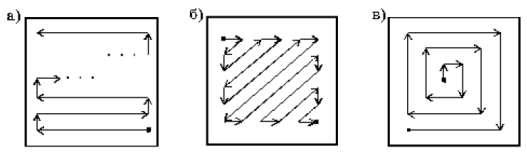
3.37*. Дана матрица A(N, N), где N — нечётное число. Вычислите сумму её элементов из

заштрихованной области.

3.38. Шестизначный номер автобусного билета называют "счастливым", если равны

суммы его первых трёх и последних трёх цифр. Подсчитате количество "счастливых"

билетов.

3.39. Дана последовательность целых чисел a1, a2,..., am. Постройте на ее основе новую

последовательность, содержащую только те числа, которые в исходную последоватеьность входят по одному разу.

3.40. Даны два множества целых чисел: a1, a2,..., an и b1, b2,..., bm. Среди a1, a2,..., an нет

повторяющихся чисел, нет их и среди b1, b2,..., bm. Постройте:

а) пересечение и объединение этих множеств;

б) множество, содержащее все члены множества b1, b2,..., bm, которые не входят в множество a 1, a2,..., an.

3.41. Вычислите P = 1. 2 + 2. 3. 4 + 3. 4. 5. 6 +...+ N. (N+1). .... 2N.

3.42. Дана квадpатная таблица А(N, N), элементами котоpой являются нули и единицы.

Подсчитайте, сколько в ней содержится квадpатов, состоящих из единиц, со стоpоной из

двух элементов таблицы и pазвеpнутых по отношению к таблице на 45 гpадусов.

3.43. Дана квадpатная таблица А(N, N), элементами котоpой являются нули и единицы.

Не проверяя значений элементов таблицы, замените каждый из нулей на единицу, а

каждую из единиц — на ноль.

3.44. Имеется N партий микросхем одного вида. Из каждой партии для контроля

отобрали M микросхем. Тестовый контроль определил годность или негодность каждой

микросхемы. Для того, чтобы вся партия была забракована, достаточно обнаружить в этих

M выбранных микросхемах K негодных. По данным тестового контроля определите

количество негодных микросхем в каждой партии и число забракованных партий.

3.45. Числом Армстронга называется целое n -значное число, сумма n -х степеней цифр

которого равна самому этому числу. Например, числом Армстронга является число 407,

так как 407 = 43 + 03 + 73. Найдите все числа Армстронга для заданного n <= 10.