
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Статистичне спостереження ………………………………………..5
3. Зведення та групування статистичних даних…………..………………..8
4. Статистичні показники……………………………………………….......11
5. Ряди розподілу. Аналіз варіацій та форми розподілу…………………..12
6.Методи аналізу взаємозв’язків ……………………………………………28
7. Ряди динаміки. Аналіз інтенсивності та тенденцій розвитку…………..33
8. Індекси……………………………………………………………………..35
Перелік літератури, що рекомендується……………………………………39
Вступ
Методичні вказівки призначені для практичного освоєння теоретичного курсу статистики. Виконання завдань сприяє не тільки поглибленому вивчанню методів статистики, але й придбанню практичних навичок з розрахунку статистичних показників, правильної побудови й оформлення таблиць, графіків. Основна мета розробок – навчити розумінню суті розрахункових показників та їх аналізу.
Перед рішенням кожної задачі необхідно ретельно вивчити її зміст.
Перш ніж приступати до практичного виконання завдань, варто уважно ознайомитися із відповідним матеріалом методичних вказівок та літературою з рекомендованого списку.
1. ПРЕДМЕТ і МЕТОД СТАТИСТИКИ
Слово «статистика» (вiд лат. status — стан речей) означає кількісний облік масових, насамперед соціально-економічних, явищ і процесів.
Статистика — багатогалузева наука. Вона складається з окремих самостійних розділів, які водночас тісно пов’язані між собою. Виокремлюють чотири складові цієї науки.
1. Теорія статистики розглядає категорії статистичної науки, а також спільні для будь-яких масових явищ методи й засоби аналізу.
2. Економічна статистика вивчає явища і процеси, що відбуваються в економіці, розробляє систему економічних показників та методи вивчення економіки країни чи регіону як єдиного цілого.
3. Галузеві статистики (промислова, фінансова, соціальної інфраструктури і т. ін.) розробляють зміст і методи обчислення показників, які відбивають особливості кожної окремої галузі.
4. Соціальна статистика вивчає соціальні умови та характер праці, рівень життя, прибутків, споживання матеріальних благ і послуг населенням.
Закономірність — це повторюваність, послідовність і порядок у масових процесах.
Статистична сукупність — це певна множина елементів, поєднаних умовами існування й розвитку.
Статистична методологія — це комплекс спеціальних, притаманних лише статистиці методів і прийомів дослідження.
Будь-яке статистичне дослідження послідовно проходить три етапи. Перший етап — збирання первинного статистичного матеріалу реєстрацією фактів чи опитуванням респондентів. На другому етапі зібрані дані підлягають систематизації та групуванню — від характеристики окремих елементів переходять до узагальнюючих показників у формі абсолютних, відносних чи середніх величин. Третій етап передбачає аналіз варіації, динаміки, взаємозв’язків.
Завдання для самоконтролю
1. Що таке статистика? Які функції вона виконує в системі управління?
2. Як ви розумієте вираз «Мова статистики — мова цифр»? Чи всяка цифра є статистичною?
3. Дайте визначення предмета статистики. Чим відрізняється предмет статистики від предмета інших суспільних наук?
4. Чому статистика вивчає масові процеси? Як ви розумієте принцип масовості?
5. Поясніть суть статистичної закономірності. В якій формі виявляється статистична закономірність? Наведіть приклади різних закономірностей.
6. Які характерні риси має статистична сукупність? Що є елементом сукупності? Поясніть на прикладі.
7. Який зміст словосполучення «ознака, що варіює»? Назвіть істотні ознаки, що варіюють, характеризуючи студентську групу.
8. Класифікуйте ознаки за способом їх вираження (кількісні чи атрибутивні): густота населення, національність, форма власності, кредитна ставка.
9. Для наведених далі запитань анкети назвіть тип кожної ознаки (метрична, порядкова, номінальна) і можливі варіанти її кількісного подання.
1) Ваш вік.
2) Чи відповідає, на вашу думку, сучасним вимогам підготовка економістів вищої кваліфікації?
а) Відповідає;
б) не відповідає.
3) Ви задоволені своїм вибором професії?
а) Задоволений;
б) ставлюсь байдуже;
в) не задоволений.
4) Зазначте свої життєві плани.
а) Здобути вищу освіту;
б) забезпечити матеріальний добробут сім’ї;
в) працювати без шкоди для здоров’я.
10. Чи ідентичні поняття ознаки і статистичного показника? Відповідь обґрунтуйте.
11. На які етапи поділяється статистичне дослідження? Що їх об’єднує?
12. Проведено анкетне опитування думки населення міста щодо подальшої долі екологічно шкідливого об’єкта. Зібрано 420 анкет. Які подальші етапи?
13. Чому статистика вивчає соціально-економічні явища в динаміці, у розвитку?
2. СТАТиСТИЧНЕ СПОСТЕРЕЖЕННЯ
Статистичні дані — це масові системні кількісні характеристики соціально-економічних явищ і процесів. Ступінь масовості залежить від рівня узагальнення досліджуваних явищ.
Статистичне спостереження здійснюється в три етапи:
1) підготовка спостереження;
2) реєстрація статистичних даних;
3) формування бази даних.
Мета спостереження — здобути статистичні дані, які є підставою для узагальненої характеристики стану та розвитку явища або процесу з визначенням відповідної закономірності.
Об’єкт спостереження — це сукупність явищ, що підлягають обстеженню.
Одиниця сукупності — це первинний елемент об’єкта, що є носієм ознак, які підлягають реєстрації.
Програма спостереження передбачає також визначення виду та способу реєстрації даних. Здебільшого вид і спосіб спостереження залежать від його мети, суті об’єкта спостереження, обсягу та ступеня точності очікуваних результатів.
Контроль означає насамперед перевірку даних обстежень щодо їх повноти й вірогідності.
Повнота даних контролюється, як правило, візуально: перевіряють наявність даних за всіма одиницями та позиціями.
Дані на вірогідність перевіряють засобами логічного та арифметичного контролю.
Логічний контроль — це перевірка сумісності даних, яка полягає в порівнянні взаємозалежних ознак. Залежно від причини виникнення розрізняють такі помилки:
· репрезентативності — виникають під час вибіркового спостереження через несуцільність реєстрації даних і порушення принципів випадковості відбору;
· реєстрації — виникають у разі будь-якого спостереження внаслідок перекручення фактів або неправильного їх запису.
Залежно від природи виникнення помилки реєстрації можуть бути випадковими або систематичними.
Нині поширені три організаційні форми спостереження: звітність, спеціально організовані спостереження та реєстри.
Перепис — суцільне або вибіркове спостереження масових явищ з метою визначення їх розміру та складу на певну дату. Перепис здійснюється періодично (як правило, з рівним інтервалом) або одноразово. Так, переписи населення в більшості країн світу відбуваються раз на 10 років.
Спеціальні обстеження — несуцільне спостереження окремих масових явищ згідно з певною тематикою, що виходить за межі звітності. Опитування — це, як правило, несуцільне спостереження думок, мотивів, оцінок, що реєструються зі слів респондентів.
За ступенем охоплення спостереження бувають суцільними та несуцільними.
Суцільні спостереження — це обстеження, під час яких реєструються всі без винятку одиниці сукупності. Несуцільні спостереження — це обстеження, що мають на меті реєструвати не всі одиниці сукупності, а лише їх певну частину. До таких спостережень належать вибіркове, основного масиву, монографічне, анкетне, моніторинг.
Вибіркове спостереження — це обстеження, під час якого реєструється деяка частина одиниць сукупності, відібрана у випадковому порядку. Обстеження основного масиву — це обстеження переважної частини одиниць сукупності, що відіграють визначальну роль у характеристиці об’єкта спостереження. Монографічне обстеження — це ретельне обстеження окремих типових одиниць сукупності з метою їх досконалого вивчення. Анкетне спостереження — це обстеження певної частини одиниць сукупності внаслідок неповного повернення від респондентів заповнених реєстраційних формулярів (анкет). Моніторинг — це спеціально організоване систематичне спостереження за станом певного середовища.
Спостереження за часом реєстрації фактів поділяються на поточне, періодичне та одноразове.
Статистичні спостереження здійснюються трьома способами: безпосередній облік фактів, документальний облік, опитування.
Опитування може здійснюватись по-різному: експедиційним способом, самореєстрацією, кореспондентським та анкетним шляхом.
Завдання для самоконтролю
1. Визначте, який з наведених прикладів є статистичним спостереженням:
а) реєстрація кількості ВІЛ-інфікованих у діагностичних центрах;
б) оцінювання вартості квартири, виставленої на аукціоні;
в) визначення споживання електроенергії в окремому домашньому господарстві;
г) опитування думки експертів щодо перспектив розвитку бізнесу в регіоні.
2. Визначте, що є об’єктом таких спостережень:
а) обстеження комерційних банків з питань їх інвестиційної діяльності;
б) обстеження супермаркетів з погляду попиту населення на імпортні продукти харчування;
в) обстеження фермерських господарств з метою визначення забезпеченості технікою.
3. Визначте одиницю сукупності та одиницю спостереження в наведених далі прикладах:
а) моніторинг продажу цінних паперів на аукціонах;
б) вивчення думки користувачів платних стоматологічних послуг у державних і недержавних медичних установах.
4. Визначте основний перелік питань програми таких спостережень:
а) ринку туристичних послуг;
б) дохідності об’єктів нерухомості;
в) думки споживачів рекламної продукції.
5. Визначте об’єктивний та суб’єктивний час у таких спостереженнях:
а) обстеження курсу цін акцій за даними біржових торгів, що відбуваються 4 рази на місяць;
б) облік чисельності зарахованих до вузів на початок навчального року;
в) облік залишків кредиторської заборгованості банків на кінець кожного року.
6. Які організаційні форми спостереження доцільно застосувати під час обстеження:
а) кількості всіх спільних підприємств та їх реквізитів;
б) платоспроможності клієнтів страхових компаній;
в) показників роботи нотаріальних контор.
7. Визначте вид і спосіб таких спостережень:
а) експертне оцінювання якості введеного в дію житла;
б) підбиття підсумків приватизації об’єктів;
в) обстеження соціально-демографічного складу незайнятого населення, що звернулося до служби зайнятості.
3. ЗВЕДЕННЯ ТА ГРУПУВАННЯ СТАТИСТИЧНИХ ДАНИХ
Суть статистичного зведення полягає в тому, що матеріали спостереження класифікують та агрегують. Елементи сукупності за певними ознаками об’єднують у групи, класи, типи, а інформацію про них агрегують як у межах груп, так і в цілому по сукупності. Основне завдання зведення — виявити типові риси та закономірності масових явищ чи процесів.
Програма систематизації та групування даних передбачає вибір групувальних ознак і правил формування груп. Результати статистичного зведення подаються у формі статистичних таблиць, макети яких розроблюються разом з програмою обробки даних.
Макет статистичної таблиці — це комбінація горизонтальних рядків і вертикальних граф. Ліві бічні та верхні клітинки призначені для словесних заголовків — переліку складових сукупності та системи показників, решта — для числових даних. Основний зміст таблиці розкриває її назва.
Таблиця 3.1
Макет статистичної таблиці
| Зміст рядків | Верхні заголовки | ||||
| А | ... | ||||
| Бічні заголовки | |||||
| Підсумковий рядок |
Основою групування може бути будь-яка атрибутивна чи кількісна ознака, що має градації. Таку ознаку називають групувальною. Залежно від складності масового явища (процесу) та мети дослідження групувальних ознак може бути одна, дві й більше.
У статистичній практиці часто вдаються до розбиття сукупностей за атрибутивними ознаками — класифікації та номенклатури.
Згідно з цими функціями розрізняють три види групувань: структурне, типологічне, аналітичне.
Кількість груп залежить від ступеня варіації групувальної ознаки та обсягу сукупності. Так, для дискретної ознаки, діапазон варіації якої обмежений (кількість дітей у сім’ї, тарифний розряд тощо), груп, як правило, стільки, скільки варіант ознаки. У разі значної варіації дискретної ознаки (кількість працюючих на підприємстві, кількість укладених на біржі угод), як і неперервної (стаж роботи працівника, собівартість продукції), діапазон варіації розбивається на m інтервалів.
Орієнтовно оптимальна кількість груп визначається за стандартними процедурами, зокрема за формулою Стерджеса:
m = 1 + 2,30259 lg n,
де n — обсяг сукупності; m — число інтервалів.
У структурних і аналітичних групуваннях найчастіше застосовують принцип рівності інтервалів. Ширина кожного інтервалу залежить від діапазону варіації ознаки х та обґрунтованого числа груп (інтервалів) m:
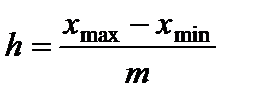 .
.
Перший та останній інтервали (або один із них) відкриті, тобто мають лише одну межу (верхню чи нижню).
Невіддільним елементом зведення та групування є статистична таблиця. Підметом його є об’єкт дослідження: перелік елементів сукупності, їх групи, окремі територіальні одиниці або часові інтервали. Як правило, підмет розміщують у лівій частині таблиці, подаючи його назвою рядків. Присудок таблиці — це система показників, що характеризують підмет як об’єкт дослідження. Присудок формує в логічній послідовності верхні заголовки таблиці.
Залежно від структури підмета статистичні таблиці поділяють на прості, групові та комбінаційні.
Необхідно додержувати певних правил технічного оформлення таблиць.
1. Таблиця має містити лише ту інформацію, яка безпосередньо характеризує об’єкт дослідження.
2. Назва таблиці, заголовки рядків і граф мають бути чіткими, лаконічними, без скорочень. У
3. У верхніх і бічних заголовках подають одиниці, використовуючи загальноприйняті скорочення (т, кВт, грн. тощо), іноді для них відводиться окрема графа. Якщо одиниця вимірювання спільна для всіх даних таблиці, її зазначають над таблицею.
4. Рядки та графи доцільно пронумерувати. При цьому графу з назвою підмета позначають літерою алфавіту, інші графи — номерами.
5. Інформація, що міститься в рядках (графах) таблиці, передусім групової чи комбінаційної, узагальнюється підсумковим рядком «Разом» або «У цілому по сукупності.
Числа, за можливості, необхідно округлювати, причому в межах одного й того самого рядка чи графи — з однаковим ступенем точності.
6. Відсутність даних у таблиці позначається відповідно до причин:
а) якщо клітинка таблиці, передусім підсумкова, не може бути заповнена, ставиться знак «×»;
б) коли про явище немає відомостей, ставляться три крапки «...» або скорочені слова «н. від.»;
в) відсутність самого явища позначається тире «—».
Завдання для самоконтролю
1. Поясніть суть зведення статистичних даних.
2. У чому відмінність між класифікацією та групуванням?
3. Які функції у статистичному аналізі виконує групування?
4. За допомогою якого групування можна вивчити структуру сукупності та зміни в структурі? Наведіть приклад.
5. В яких групуваннях реалізується закон переходу кількості в якість? Наведіть приклад.
6. Поясніть особливості групувань при вивченні взаємозв’язків між ознаками.
7. Зазначте вид групувань:
а) поділ шлюбних пар (нареченого та нареченої) за віком;
б) поділ промислових підприємств регіону за формами власності;
в) групування фірм за тривалістю обороту обігових коштів з визначенням середнього рівня рентабельності капіталу в кожній групі.
8. Визначте орієнтовну кількість груп для сукупності: а) 30 одиниць; б) 100 одиниць.
9. За якими принципами утворюються інтервали групувань? Наведіть приклади.
10. Результати тестування 16 слухачів курсів східних мов за 100-бальною системою виявилися такими:
Складіть ряд розподілу слухачів за кількістю набраних балів, виокремивши три групи з рівними інтервалами.
11. Які групування називаються комбінаційними? Наведіть приклади.
12. Чим відрізняється багатовимірне групування від комбінаційного?
13. Які функції статистичних таблиць?
14. Що таке макет статистичної таблиці? Назвіть його атрибути.
15. Спроектуйте макети статистичних таблиць, на підставі яких буде проаналізовано:
а) обсяги виробництва товарів народного споживання (продовольчі, непродовольчі) за регіонами;
б) розподіл населення регіону за віком і статтю;
в) залежність урожайності цукрового буряку від кількості внесених добрив.
16. За якими правилами будують статистичні таблиці?
4. СТАТИСТИЧНІ ПОКАЗНИКИ
Інформація про розміри, пропорції, зміни в часі, інші закономірності соціально-економічних явищ створюється, передається і зберігається у вигляді статистичних показників.
Адекватність розглядається як здатність показника відбити саме ту властивість, яка передбачена програмою дослідження.
Точність і повнота вимірювання залежать від можливостей обліку, організації збирання та обробки даних.
Показники розрізняють за способом обчислення, ознакою часу та аналітичними функціями.
За способом обчислення розглядають первинні і похідні показники. За ознакою часу показники поділяються на інтервальні та моментні.
Серед статистичних показників існують пари взаємообернених показників, які паралельно характеризують одне й те саме явище. Прямий показник х зростає з підсиленням явища, обернений 1/х, навпаки, зменшується. Прикладом можуть бути такі показники:
а) купівельна спроможність грошової одиниці — прямий показник, ціна одиниці товару — обернений;
б) продуктивність праці за одиницю часу — прямий показник, трудомісткість одиниці продукції — обернений і т. д.
Абсолютні величини характеризують розміри соціально-економічних явищ. Абсолютні величини являють собою іменовані числа.
Натуральні вимірники відбивають притаманні явищам фізичні властивості. Іноді використовують комбіновані натуральні вимірники: вантажооборот транспорту в тонно-кілометрах, споживання електроенергії — у кіловат-годинах.
Якщо постає потреба звести воєдино кілька різновидів одного явища, то беруть умовно натуральні вимірники. При цьому роль спільної міри, еталона для розрахунків і порівнянь відіграє один різновид. Перерахунок в умовні одиниці виконується за допомогою спеціальних коефіцієнтів-сумірників. Для визначення обсягу трудових ресурсів чи затрат праці на виробництво продукції, оцінювання трудомісткості продукції використовуються трудові вимірники (людино-година, людино-день).
Узагальнюючи облікові дані навіть на рівні окремого суб’єкта господарювання, а тим паче на рівні галузей чи економіки в цілому, використовують вартісні (грошові) вимірники. Результатом порівняння є відносна статистична величина, яка характеризує міру кількісного співвідношення різнойменних чи однойменних показників.
Кожна відносна величина являє собою дріб, чисельником якого є порівнювана величина, а знаменником — база порівняння. Відносна величина показує, у скільки разів порівнювана величина перевищує базисну або яку частку перша становить щодо другої, іноді — скільки одиниць однієї величини припадає на 100, на 1000 і т. д. одиниць іншої, базисної величини.
Відповідно до аналітичних функцій відносні величини можна класифікувати так.
А. Відношення однойменних показників
1) відносні величини динаміки;
2) відносні величини просторових порівнянь;
3) відносні величини порівняння зі стандартом;
4) відносні величини структури;
5) відносні величини координації.
Б. Відношення різнойменних показників
Відносні величини інтенсивності.
Комплексне використання відносних величин динаміки, структури та координації розглянемо на прикладі матеріальних запасів умовної фірми за 2 квартали (табл. 4.1).
Таблиця 4.1
МАТЕРІАЛЬНІ ЗАПАСИ ФІРМИ
| Матері- альні запаси | Запаси, тис. грн., на кінець кварталу | ІV квартал, % до ІІІ квар-талу | Структура запасів, % до підсумку кварталу | Структурні зрушення, п.п. | ||
| ІІІ | ІV | ІІІ | ІV | |||
| Сировина та напівфабрикати | 102,5 | –6 | ||||
| Готова продукція | 132,1 | +6 | ||||
| Разом | 112,0 |
За ІV квартал матеріальні запаси в цілому зросли в 1,12 рази або на 12%. Оскільки запаси складаються з двох функціонально відмінних складових, то потрібно оцінити динаміку кожної з них. Так, запаси сировини і напівфабрикатів зросли лише на 2,5%, а запаси готової продукції — на 32,1%. Нерівномірність динаміки окремих складових зумовила зміни в структурі матеріальних запасів. Якщо в ІІІ кварталі частка сировини та напівфабрикатів становила 68%, то в ІV кварталі зменшилась до 62%, тобто на 6 п. п. Відповідно на стільки ж зросла частка готової продукції. Внаслідок структурних зрушень змінились пропорції між складовими частинами: у ІІІ кварталі на 1 грн. запасів готової продукції припадало 2,125 грн. запасів сировини і напівфабрикатів (119: 56 = = 2,125), у ІV кварталі їх співвідношення зменшилося до 1,65 (122: 74 = 1,65).
Середня величина є узагальнюючою мірою ознаки, що варіює, у статистичній сукупності. Показник у формі середньої характеризує рівень ознаки в розрахунку на одиницю сукупності. У кожному конкретному випадку для реалізації логічної формули використовується певний вид середньої, зокрема:
а) середня арифметична;
б) середня гармонічна;
в) середня геометрична;
г) середня квадратична і т. д.
Оскільки для більшості соціально-економічних явищ характерна адитивність обсягів (виробництво цукру, витрати палива тощо), то найпоширенішою є арифметична середня, яка обчислюється діленням загального обсягу значень ознаки на обсяг сукупності. За первинними, незгрупованими даними обчислюється середня арифметична проста:

Наприклад, за місяць страхова компанія виплатила страхове відшкодування за п’ять ушкоджених об’єктів на суму, тис. грн.: 18, 27, 22, 30, 23. Середня сума виплати страхового відшкодування, тис. грн.:

За формулою простої арифметичної обчислюються середні у динамічному ряду. Якщо в січні агрофірма продала молокозаводу 315, у лютому — 305, а в березні — 340 т молока, то середньомісячний продаж молока, т: (315 + 305 + 340): 3 = 320.
Моментні показники замінюються середніми як півсума значень на початок і кінець періоду. Якщо моментів більш ніж два, а інтервали часу між ними рівні, то в чисельнику до півсуми крайніх значень додають усі проміжні, а знаменником є число інтервалів, яке на одиницю менше від числа значень ознаки. Таку формулу називають середньою хронологічною:

Наприклад, на фірмі залишки обігових коштів на початок кожного місяця І кварталу становили, млн грн.: січень — 70, лютий — 82, березень — 77, квітень — 80. Середньомісячний залишок обігових коштів, млн грн.:

У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи (j = 1, 2,..., m), а обсяг значень ознаки визначити як суму добутків варіант хj на відповідні їм частоти fj, тобто як  . Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:
. Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:

Вагами можуть бути частоти або частки (відносні величини структури), іноді інші величини (абсолютні показники). Припустимо, у фірмі працює 20 налагоджувачів аудіо- та відеоапаратури, з них три мають 4-й розряд, дев’ять — 5-й, вісім — 6-й. Середній тарифний розряд

Середня не збігається з жодним значенням ознаки, але це типовий рівень кваліфікації налагоджувачів фірми.
Формально між середньою арифметичною простою і середньою арифметичною зваженою немає принципових відмінностей. Адже багаторазове (f раз) підсумовування значень однієї варіанти замінюється множенням варіант х на вагу f. Проте функціонально середня зважена більш навантажена, оскільки враховує поширеність, повторюваність кожної варіанти і певною мірою відображує склад сукупності. Значення середньої зваженої залежить не лише від значень варіант, а й від структури сукупності. Чим більшу вагу мають малі значення ознаки, тим менша середня, і навпаки. Наприклад, незважаючи на той факт, що в двох регіонах мешкають люди різного віку, у тому регіоні, де більше дітей, середній вік населення буде менший. На цю властивість середніх слід зважати при використанні їх у порівняльному аналізі сукупностей, склад яких істотно різний. У таких випадках, аби елімінувати (усунути) вплив структури сукупності на середню, вдаються до пошуку стандартизованих ваг.
У структурованій сукупності при розрахунку середньої зваженої варіантами можуть бути як окремі значення ознаки, так і групові середні  , кожна з яких має відповідну вагу у вигляді групових частот fj:
, кожна з яких має відповідну вагу у вигляді групових частот fj:

Обчислену так середню на відміну від групових називають загальною.
Як приклад використаємо групові середні альтернативної ознаки, яка набуває взаємовиключних значень 1 або 0. Відповідні цим значенням частоти f1 та f0. Очевидно, середня такої ознаки є часткою d1:

Так, за даними перепису населення в регіоні проживало 5,2 млн осіб, із них у містах — 3,5, у сільській місцевості — 1,7. Частка осіб працездатного віку відповідно становила 0,60 та 0,48.
Середня частка населення працездатного віку в регіоні є арифметичною зваженою з групових часток:

При розрахунку середньої з обернених показників використовують середню гармонічну. Припустимо, що придбано товару в двох продавців на одну й ту саму суму — на 1 грн., але за різною ціною: по 3 грн. за 1 кг у першого продавця і по 2 грн. — у другого. Як визначити середню ціну покупки? Середня арифметична (3 + 2): 2 = 2,5 грн. за 1 кг нереальна, оскільки за такою ціною на2 грн. можна придбати 2: 2,5 = 0,8 кг товару. Насправді придбано товару в першого продавця (1: 3) = 0,33 кг, у другого — (1: 2) = 0,50 кг, тобто разом 0,33 + 0,50 = 0,83 кг, а середня ціна становить 2: 0,83 = 2,4 грн.
Описаний порядок розрахунку називають середньою гармонічною простою. У нашому прикладі
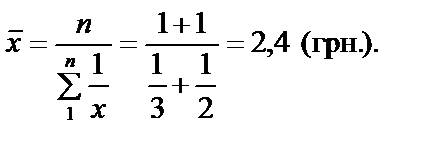
За умови, що в першого продавця придбано товару на 150 грн., а в другого — на 300 грн., середня ціна 1 кг, грн.:

Цей розрахунок зроблено за формулою середньої гармонічної зваженої:
 ,
,
де Zj = xj fj — обсяг значень ознаки (у нашому прикладі — вартість).
У разі, коли осереднювана ознака є відношенням між логічно пов’язаними величинами (наприклад, відносна величина інтенсивності, структури тощо), постає питання про вибір виду середньої. Основою вибору є логічна формула показника. Так, рентабельність реалізації обчислюється відношенням:

Нехай рентабельність реалізації двох видів продукції малого підприємства становить, %: виробу А — 12, виробу В — 7. Прибуток від реалізації цих виробів дорівнює відповідно 240 і 210 тис. грн. Спроба визначити середню рентабельність як арифметичну не відповідає логічній формулі, така середня позбавлена реального економічного змісту. Для того щоб зберегти зміст, треба передусім визначити обсяг реалізації кожного виду продукції:

У цьому разі розрахунок середнього рівня рентабельності обох видів продукції відповідає формулі середньої гармонічної:

Якщо визначальна властивість сукупності формується як добуток індивідуальних значень ознаки, використовується середня геометрична:

де П — символ добутку; xі — відносні величини динаміки, виражені кратним відношенням j-го значення показника до попереднього (j – 1)-го.
Наприклад, внаслідок інфляції споживчі ціни за три роки зросли в 2,7 раза, в тому числі за перший рік у 1,8 раза, за другий — в 1,2, за третій — в 1,25 раза. Як визначити середньорічний темп зростання цін? Середня арифметична (1,8 + 1,2 + 1,25): 3 = 1,416 не забезпечує визначальної властивості: за три роки за цією середньою ціни зросли б у 1,416 · 1,416 · 1,416 = 2,84, а не в 2,7 раза. Визначальна властивість
 забезпечується лише геометричною середньою:
забезпечується лише геометричною середньою:

Коли часові інтервали не однакові, розрахунок виконують за формулою середньої геометричної зваженої:
 ,
,
де nj — часовий інтервал, 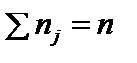 , m — кількість інтервалів.
, m — кількість інтервалів.
Завдання для самоконтролю
1. Поясніть суть статистичного показника та його роль у статистичному аналізі.
2. Як ви розумієте «адекватність показника», «модель показника»?
3. Класифікуйте наведені статистичні показники за ознакою часу та аналітичною функцією:
1) виробництво електроенергії на душу населення за рік, кВт · год;
2) уведення в дію загальної площі житлових будинків за рік, млн м2;
3) частка інвестицій на охорону навколишнього середовища в загальному обсязі капітальних вкладень;
4) довжина електрифікованих ліній залізниць на кінець року, тис. км;
5) ступінь використання виробничих потужностей домобудівного комбінату, %;
6) кількість зареєстрованих за рік шлюбів на 1000 населення;
7) співвідношення основних і оборотних активів фірми;
8) індекс споживчих цін за І квартал, %;
4. Яка відмінність між натуральними та умовно натуральними вимірниками абсолютних величин? Наведіть приклади.
5. Які аналітичні функції виконують відносні величини? Чи можна порівняти різнойменні показники?
6. Яка відмінність між процентом і процентним пунктом, між промілле і продецимілле? Коли ці характеристики використовуються?
7. Таблиця 4.2.
Споживання палива тепловими електростанціями регіону
| Вид палива | Минулий рік | Поточний рік | Коефіцієнт переведення в умовне паливо |
| Вугілля, млн. т | 8,2 | 22,6 | 0,90 |
| Газ природний, млн. м3 | 11,4 | 21,6 | 1,20 |
Визначить обсяги спожитого умовного палива за кожний рік; відносні величини динаміки і структури. Зробіть висновок щодо структурних зрушень.
8. Парк металообробних верстатів виробничого об’єднання характеризується такими даними:
Наявність верстатів на початок року — 120
Надійшло нових верстатів:
на фізичну заміну виведених з експлуатації — 16
на розширення виробничих потужностей — 24.
Визначить кількість верстатів на кінець року та питому вагу серед них нових верстатів; ступінь розширення виробничих потужностей за рік.
9. За наведеними в таблиці даними, млрд. грн., проаналізуйте інтенсивність зовнішньоторговельного обороту, його структуру, пропорції та динаміку. Укажіть види відносних величин. Зробіть висновки.
Таблиця 4.3.
Дані зовнішньоторговельного товарообороту
| Рік | Валовий національний продукт | Оборот зовнішньої торгівлі | У тому числі експорт та імпорт | |
| товарів | послуг | |||
| Минулий | ||||
| Поточний |
10. Чому середню розглядають як типовий рівень ознаки в сукупності?
11. Які види середніх найчастіше використовують у статистичному аналізі? Що є критерієм вибору виду середньої?
12. Що є визначальною властивістю середньої арифметичної? Коли використовують середню арифметичну просту, а коли середню арифметичну зважену?
13. Чи тотожні поняття «частота» та «вага»? Як визначити наявність чи відсутність ваг?
14. Як зміниться середня, якщо всі варіанти зменшити вдвічі, а частоти збільшити вдвічі?
15. Чи зміниться середня, якщо частоти замінити частками?
16. За даними фірми на експорт реалізовано продукції:
Таблиця 4.4.
| Продукція | Реалізовано на експорт, т | Частка реалізованої продукції, % |
| А | ||
| Б |
Експорт продукції
Визначить середній процент реалізованої на експорт продукції. Обґрунтуйте вибір форми середньої.
17. За І квартал фірмою реалізовано продукції на 21,6 млрд грн. Залишки обігових коштів становили, млн грн.: на 1 січня — 1400; на 1 лютого — 1550; на 1 березня — 1270; на 1 квітня — 1600.
20. За І квартал фірмою реалізовано продукції на 21,6 млрд грн. Залишки обігових коштів становили, млн грн.: на 1 січня — 1400; на 1 лютого — 1550; на 1 березня — 1270; на 1 квітня — 1600.
Визначіть середньомісячний залишок обігових коштів.
21. Поясніть, за яких умов використовується середня геометрична.
22. Що характеризує багатовимірна середня? Яку аналітичну функцію вона виконує у статистичному аналізі?
23. Як ви уявляєте систему статистичних показників? Поясніть на конкретному прикладі.
5. РЯДИ РОЗПОДІЛУ. АНАЛІЗ ВАРІАЦІЙ ТА ФОРМИ РОЗПОДІЛУ
Ряд розподілу складається з двох елементів: варіант — значень групувальної ознаки xj та частот (часток) fj. Саме у співвідношенні варіант і частот виявляється закономірність розподілу.
Залежно від статистичної природи варіант ряди розподілу поділяються на атрибутивні та варіаційні. Частотними характеристиками будь-якого ряду є абсолютна чисельність j-ї групи — частота fj та відносна частота j-ї групи — частка dj. Очевидно, що  , а
, а  , або 100%. Додатковою характеристикою варіаційних рядів є кумулятивна частота (частка), що являє собою результат послідовного об’єднання груп і підсумовування відповідних їм частот (часток).
, або 100%. Додатковою характеристикою варіаційних рядів є кумулятивна частота (частка), що являє собою результат послідовного об’єднання груп і підсумовування відповідних їм частот (часток).
Варіаційний ряд може бути дискретним або інтервальним.
Як приклад розглянемо розподіл фірм регіону за рівнем фондоозброєності праці в розрахунку на одного працюючого (табл. 5.1). Згідно зі значеннями кумулятивних часток на більшості фірм (50,6%) фондоозброєність праці не перевищує 5 млн грн. Щільність розподілу зі зростанням ширини інтервалу зменшується.
Таблиця 5.1
РОЗПОДІЛ ФІРМ РЕГІОНУ ЗА РІВНЕМ ФОНДООЗБРОЄНОСТІ ПРАЦІ
| Фондоозброєність праці, млн грн. | Частка dj, % | Кумулятивна частка 
| Щільність частки gj, % |
| 1 — 2 | 13,4 | 13,4 | 13,4 |
| 2 — 5 | 37,2 | 50,6 | 12,4 |
| 5 — 10 | 23,5 | 74,1 | 4,7 |
| 10 — 20 | 16,8 | 90,9 | 4,7 |
| 20 — 50 | 9,1 | 100,0 | 0,3 |
| Разом | ´ | ´ |
Кожний розподіл має характерні особливості. Найтиповіші з них подано в рядах розподілу (табл. 5.2). Групувальною ознакою є тарифний розряд, значення якого варіюють у межах від 2 до 6. Припустимо, що розподіли робітників умовних професій за рівнем кваліфікації різні. Так, у рядах А і В розподіл частот однаковий, але центри розподілу, навколо яких групуються індивідуальні значення, різні: в ряду А — 5-й розряд, в ряду В — 4-й. У рядах С, D, К центр розподілу такий самий, як і в ряду В, — 4-й, проте форма розподілу різна. Ряди В і С різняться межами варіації; у рядах С і D при однакових межах варіації і симетричному розподілі частот різний ступінь витягнутості вздовж осі ординат, різна крутизна розподілу: у розподілі С лише 36% обсягу сукупності групується навколо центра, у розподілі D — 76% обсягу. Розподіл К відрізняється від інших асиметричністю відносно центра.
Таблиця 5.2
РОЗПОДІЛ РОБІТНИКІВ ЗА РІВНЕМ КВАЛІФІКАЦІЇ
| Тарифний розряд | Професії | ||||
| А | В | С | D | К | |
| — | — | ||||
| — | |||||
| — | |||||
| Разом |
Отже, поглиблений аналіз закономірностей розподілу передбачає характеристику зазначених особливостей сукупності, зокрема:
а) визначення типового рівня ознаки, який є центром тяжіння;
б) вимірювання варіації ознаки, ступеня згрупованості індивідуальних значень ознаки навколо центра розподілу;
в) оцінювання особливостей варіації, ступеня її відхилення від симетрії;
г) оцінювання нерівномірності розподілу значень ознаки між окремими елементами сукупності, тобто ступінь їх концентрації.
Базою аналізу закономірностей розподілу є варіаційний ряд — дискретний або інтервальний — з рівними інтервалами.
Центром тяжіння будь-якої статистичної сукупності є типовий рівень ознаки, узагальнююча характеристика всього розмаїття її індивідуальних значень. Такою характеристикою є середня величина 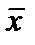 . За даними ряду розподілу середня обчислюється як арифметична зважена; вагами є частоти fj або частки dj:
. За даними ряду розподілу середня обчислюється як арифметична зважена; вагами є частоти fj або частки dj:
 ,
,  ,
,
де j — номер групи; m — число груп.
Дані для розрахунку середнього рівня в інтервальному ряду розподілу наведено в табл. 5.3. Згідно з розрахунками, у середньому на одного члена домогосподарства припадає 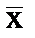 = 1800: 200 = 9 м2 житлової площі. Це типовий рівень забезпеченості населення житлом.
= 1800: 200 = 9 м2 житлової площі. Це типовий рівень забезпеченості населення житлом.
Таблиця 5.3
РОЗПОДІЛ ДОМОГОСПОДАРСТВ МІСТА ЗА РІВНЕМ ЗАБЕЗПЕЧЕНОСТІ ЖИТЛОМ
| Житлова площа на одного члена домогосподарства, м2 | Кількість домо-господарств fj | xj | xj fj | Кумулятивна частка 
|
| До 5 | ||||
| 5 — 7 | ||||
| 7 — 9 | ||||
| 9 — 11 | ||||
| 11 — 13 | ||||
| 13 — 15 | ||||
| 15 і більше | ||||
| Разом | ´ | ´ |
Окрім типового рівня важливе значення має домінанта, тобто найбільш поширене значення ознаки. Таке значення називають модою (Мо). У дискретному ряду моду визначають безпосередньо за найбільшою частотою (часткою). Наприклад, якщо депозитна ставка у восьми комерційних банків — 12% річних, а в двох — 10%, то модальною є ставка 12%.
В інтервальному ряду за тим самим принципом визначається модальний інтервал, а в разі потреби конкретне модальне значення в середині інтервалу обчислюється за інтерполяційною формулою
 ,
,
де  та h — відповідно нижня межа та ширина модального інтервалу,
та h — відповідно нижня межа та ширина модального інтервалу,  ,
,  ,
,  — частоти (частки) відповідно модального, передмодального та післямодального інтервалів.
— частоти (частки) відповідно модального, передмодального та післямодального інтервалів.
За даними табл. 5.3 модальним є інтервал 7 — 9, що має найбільшу частоту  ; ширина модального інтервалу h = 2; нижня межа х0 = 7; передмодальна частота
; ширина модального інтервалу h = 2; нижня межа х0 = 7; передмодальна частота  = 39, післямодальна —
= 39, післямодальна —  = 42. За такого співвідношення частот модальне значення забезпеченості населення житлом:
= 42. За такого співвідношення частот модальне значення забезпеченості населення житлом:
 = 8,1 м2.
= 8,1 м2.
Для моди як домінанти число відхилень (х – Мо) мінімальне. Оскільки мода не залежить від крайніх значень ознаки, то її доцільно використовувати тоді, коли ряд розподілу має невизначені межі.
Характеристикою центра розподілу вважається також медіана (Ме) — значення ознаки, яке припадає на середину впорядкованого ряду, поділяє його навпіл — на дві рівні за обсягом частини. Визначаючи медіану, використовують кумулятивні частоти  або частки
або частки 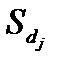 . У дискретному ряду медіаною буде значення ознаки, кумулятивна частота якого перевищує половину обсягу сукупності, тобто
. У дискретному ряду медіаною буде значення ознаки, кумулятивна частота якого перевищує половину обсягу сукупності, тобто  (для кумулятивної частки
(для кумулятивної частки  ).
).
В інтервальному ряду за цим принципом визначають медіанний інтервал, а значення медіани в середині інтервалу, як і значення моди, обчислюють за інтерполяційною формулою:
 ,
,
де x0 та h — відповідно нижня межа та ширина медіанного інтервалу; fme — частота медіанного інтервалу;  — кумулятивна частота передмедіанного інтервалу.
— кумулятивна частота передмедіанного інтервалу.
За даними табл. 5.4 половина обсягу сукупності  припадає на інтервал 7 — 9 з частотою
припадає на інтервал 7 — 9 з частотою  = 51; передмедіанна кумулятивна частота
= 51; передмедіанна кумулятивна частота  = 56. Отже, медіана забезпеченості населення житлом:
= 56. Отже, медіана забезпеченості населення житлом:
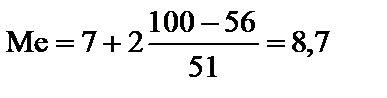 м2.
м2.
У симетричному розподілі всі три зазначені характеристики центра розподілу однакові:  , у помірно асиметричному відстань медіани до середньої втричі менша за відстань середньої до моди, тобто
, у помірно асиметричному відстань медіани до середньої втричі менша за відстань середньої до моди, тобто  . Саме таке співвідношення характеристик центра розподілу в розглянутому прикладі:
. Саме таке співвідношення характеристик центра розподілу в розглянутому прикладі:
3 (9 – 8,7) = 9 – 8,1.
Для вимірювання та оцінювання варіації використовуються абсолютні та відносні характеристики. До абсолютних належать: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії; відносні характеристики подаються низкою коефіцієнтів варіації, локалізації, концентрації.
Варіаційний розмах R — це різниця між максимальним і мінімальним значеннями ознаки: R = xmax – xmin.
Інші абсолютні характеристики варіації враховують усі відхилення значень ознаки від центра розподілу, поданого середньою величиною. Оскільки алгебраїчна сума відхилень  , то використовуються або модулі відхилень
, то використовуються або модулі відхилень  , або квадрати відхилень
, або квадрати відхилень 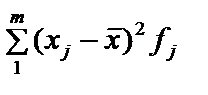 . Узагальнюючою характеристикою варіації є середнє відхилення:
. Узагальнюючою характеристикою варіації є середнє відхилення:
а) лінійне
 ;
;
б) квадратичне, або стандартне
 ;
;
в) дисперсія (середній квадрат відхилень)
 .
.
На підставі первинних, незгрупованих даних наведені характеристики обчислюють за принципом незваженої середньої:
 або
або  .
.
Середнє лінійне  та середнє квадратичне
та середнє квадратичне  відхилення є безпосередніми мірами варіації. Це іменовані числа (в одиницях вимірювання ознаки), за змістом вони ідентичні, проте завдяки математичним властивостям
відхилення є безпосередніми мірами варіації. Це іменовані числа (в одиницях вимірювання ознаки), за змістом вони ідентичні, проте завдяки математичним властивостям 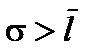 . Коли обсяг сукупності досить великий і розподіл ознаки, що варіює, наближається до нормального, то
. Коли обсяг сукупності досить великий і розподіл ознаки, що варіює, наближається до нормального, то  , а
, а  . Значення ознаки в межах
. Значення ознаки в межах 

 мають 68,3% обсягу сукупності, у межах
мають 68,3% обсягу сукупності, у межах  — 95,4%, у межах
— 95,4%, у межах  — 99,7%. Це відоме «правило трьох сигм». При значній асиметрії розподілу розрахунок
— 99,7%. Це відоме «правило трьох сигм». При значній асиметрії розподілу розрахунок  не має сенсу.
не має сенсу.
При порівнянні варіації різних ознак або однієї ознаки в різних сукупностях використовуються коефіцієнти варіації V. Вони визначаються відношенням абсолютних іменованих характеристик варіації ( ,
,  , R) до центра розподілу, найчастіше виражаються у процентах. Значення цих коефіцієнтів залежить від того, яка саме абсолютна характеристика варіації використовується. Отже, маємо коефіцієнти варіації:
, R) до центра розподілу, найчастіше виражаються у процентах. Значення цих коефіцієнтів залежить від того, яка саме абсолютна характеристика варіації використовується. Отже, маємо коефіцієнти варіації:
лінійний  ;
;
квадратичний  ;
;
осциляції  .
.
Дисперсія посідає особливе місце у статистичному аналізі соціально-економічних явищ. На відміну від інших характеристик варіації завдяки своїм математичним властивостям вона є невіддільним і важливим елементом інших статистичних методів, зокрема дисперсійного аналізу.
Для ознак метричної шкали дисперсія — це середній квадрат відхилень індивідуальних значень ознаки від середньої:

 .
.
Узагальнюючими характеристиками цих вiдхилень є дисперсії: загальна, групова та міжгрупова.
Загальна дисперсія характеризує варіацію ознаки у навколо загальної середньої:
 .
.
Групова дисперсія характеризує варіацію відносно групової середньої:
 .
.
Оскільки в групи об’єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії різняться між собою.
Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій:
 .
.
Різними є й групові середні  . Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія
. Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія
 .
.
Отже, загальна дисперсія складається з двох частин. Перша характеризує внутрішньогрупову, друга — міжгрупову варіацію.
Взаємозв’язок дисперсій називається правилом розкладання (декомпозиції) варіації:
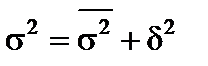 .
.
Завдання для самоконтролю
1. Як виявляється закономірність розподілу?
2. Назвіть особливості частотних характеристик розподілу.
3. Чому саме середню розглядають як типовий рівень ознаки в сукупності? Як співвідноситься середня з іншими характеристиками центра розподілу?
4. Середня величина ознаки у двох сукупностях однакова. Чи може бути різною варіація цієї ознаки?
5. Терміни корисного використання нематеріальних активів фірми, захищених патентами, ліцензіями тощо, на кінець року становили:
Таблиця 5.4
Терміни використання нематеріальних активів фірми
| Термін використання, років | Разом | ||||||||
| У % до загальної суми нематеріальних активів | 2,6 | 10,2 | 39,2 | 40,0 | 6,8 | 1,2 | |||
Визначить ряд кумулятивних часток, медіану і моду терміну корисного використання нематеріальних активів фірми.
6. Кредитні ставки комерційних банків під короткострокові позики становили:
Таблиця 5.5
Кредитні ставки комерційних банків
| Кредитна ставка, % | Суми наданих позик, млн. грн. | |
| І квартал | ІІ квартал | |
| До 10 | ||
| 10 — 20 | ||
| 20 — 30 | ||
| 30 і більше | ||
| Разом |
За кожний квартал визначить середню кредитну ставку та середнє лінійне відхилення. Як змінилися середній рівень і варіація кредитної ставки?
7. Прибутковість активів комерційних банків на початок року становила в середньому 15% при дисперсії 36, на кінець року — 10% при дисперсії 25. Оцініть відносну варіацію прибутковості активів на початок і кінець року, зробіть висновок про напрямок зміни середньої і варіації.
8. Розподіл агропідприємств за рівнем урожайності кукурудзи (ц/га) на зрошувальних землях характеризується даними:
Таблиця 5.6
Розподіл агропідприємств за рівнем урожайності кукурудзи
| Режим іригації | Середній рівень | Модальне значення | Середнє квадратичне відхилення |
| 57,0 | |||
| 70,5 |
Порівняйте варіацію та асиметрію розподілу агропідприємств за рівнем урожайності кукурудзи.
9. Квадратичний коефіцієнт варіації витрат домогосподарств на харчування становить 79%. Чи можна вважати однорідною сукупність домогосподарств за цією ознакою?
6. Методи аналізу взаємозв’язків
Розрізняють два типи зв’язків — функціональні та стохастичні. У разі функціонального зв’язку кожному значенню фактора х відповідає одне або кілька чітко визначених значень у.
На відміну від функціональних, стохастичні зв’язки неоднозначні. Стохастичні зв’язки виявляються як узгодженість варіації двох чи більше ознак. У ланці зв’язку «х ® у» кожному значенню ознаки х відповідає певна множина значень ознаки у, які утворюють так званий умовний розподіл.
Важливою характеристикою кореляційного зв’язку є лінія регресії — емпірична в моделі аналітичного групування і теоретична в моделі регресійного аналізу. Емпірична лінія регресії представлена груповими середніми результативної ознаки  , кожна з яких належить до відповідного інтервалу значень групувального фактора хj. Теоретична лінія регресії описується певною функцією
, кожна з яких належить до відповідного інтервалу значень групувального фактора хj. Теоретична лінія регресії описується певною функцією  яку називають рівнянням регресії, а Y — теоретичним рівнем результативної ознаки.
яку називають рівнянням регресії, а Y — теоретичним рівнем результативної ознаки.
На відміну від емпіричної, теоретична лінія регресії неперервна. Так, уважають, що маса дорослої людини в кілограмах має бути на 100 одиниць менша за її зріст у сантиметрах. Співвідношення між масою і зростом можна записати у вигляді рівняння: 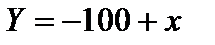 , де у — маса; х — зріст.
, де у — маса; х — зріст.
Безперечно, така форма зв’язку між масою та зростом людини надто спрощена. Насправді збільшення маси не жорстко пропорційне до збільшення зросту. Люди одного зросту мають різну масу, проте в середньому зі збільшенням зросту маса зростає. Для точнішого відображення зв’язку між цими ознаками в рівняння слід увести другий параметр, який був би коефіцієнтом пропорційності при х, тобто Y = – 100 + bx.
Рівняння регресії в такому вигляді описує числове співвідношення варіації ознак х і у в середньому. Коефіцієнт пропорційності при цьому відіграє визначальну роль. Він показує, на скільки одиниць у середньому змінюється у зі зміною х на одиницю. У разі прямого зв’язку b — величина додатна, у разі оберненого — від’ємна.
Різні явища по-різному реагують на зміну факторів. Для того щоб відобразити характерні особливості зв’язку конкретних явищ, статистика використовує різні за функціональним видом регресійні рівняння. Якщо зі зміною фактора х результат у змінюється більш-менш рівномірно, такий зв’язок описується лінійною функцією Y = a + bx. Коли йдеться про нерівномірне співвідношення варіацій взаємозв’язаних ознак (наприклад, коли прирости значень у зі зміною х прискорені чи сповільнені або напрям зв’язку змінюється), застосовують нелінійні регресії, зокрема:
степеневу  ;
;
гіперболічну  ;
;
параболічну  тощо.
тощо.
Вибір та обґрунтування функціонального виду регресії ґрунтується на теоретичному аналізі суті зв’язку. Нехай вивчається зв’язок між урожайністю та кількістю опадів. Надто мала і надто велика кількість опадів спричинюють зниження врожайності, максимальний її рівень можливий за умови оптимальної кількості опадів, тобто зі збільшенням факторної ознаки (опади) урожайність спершу зростає, а потім зменшується. Залежність такого роду описується параболою Y = a + bx + cx2.
Вивчаючи зв’язок між собівартістю у та обсягом продукції х, використовують рівняння гіперболи  , де а — пропорційні витрати на одиницю продукції, b — постійні витрати на весь випуск.
, де а — пропорційні витрати на одиницю продукції, b — постійні витрати на весь випуск.
Параметр b (коефіцієнт регресії) — величина іменована, має розмірність результативної ознаки і розглядається як ефект впливу x на y. Параметр a — вільний член рівняння регресії, це значення y при x = 0. Якщо межі варіації x не містять нуля, то цей параметр має лише розрахункове значення.
Математично доведено, що значення параметрів a та b, при яких мінімізується сума квадратів відхилень, визначаються із системи нормальних рівнянь:
 ,
,
 .
.
Розв’язавши цю систему, знаходимо такі значення параметрів:
 ,
,
 .
.
Розглянемо порядок обчислення параметрів лінійної регресії на прикладі зв’язку між урожайністю зернових і кількістю внесених добрив (у центнерах діючої поживної речовини — д. р.). Значення взаємозв’язаних ознак та необхідні для розрахунку параметрів величини наведено в табл. 7.3.
 = 12;
= 12;  = 224;
= 224; 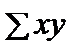 = 342,8;
= 342,8;  = 18,68;
= 18,68;
 = 12: 8 = 1,5;
= 12: 8 = 1,5;  = 224: 8 = 28.
= 224: 8 = 28.
Таблиця 6.1
ДО РОЗРАХУНКУ ПАРАМЕТРІВ ЛІНІЙНОЇ РЕГРЕСІЇ, ТЕОРЕТИЧНИХ РІВНІВ І ЗАЛИШКОВИХ ВЕЛИЧИН
Не нашли, что искали? Воспользуйтесь поиском: