
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Середні величини, їх сутність і значення.
При обробці та аналізі статистичного матеріалу, окрім порівняльних даних (у вигляді відносних величин), часто виникає необхідність одержати узагальнювальну характеристику рівня тих явищ, що вивчаються. Як правило, цифрове значення тієї або іншої ознаки у окремих одиниць сукупності неоднаково. В цьому випадку потрібно визначити середню величину ознаки, яка давала б узагальнювальну характеристику сукупності.
Наприклад, потрібно визначити, наскільки ефективна профілактична діяльність декількох територіальних підрозділів ОВД. Для цього рівень розкриваності злочинів по кожному підрозділу слід виразити одним числом і порівняти одержані величини. Ясно, що рівень, пов'язаний з індивідуальною профілактичною діяльністю кожного співробітника підрозділів, що вивчаються, не може бути використаний для такого порівняння, оскільки він різний залежно від ряду причин (кваліфікації, стажу роботи, завантаженості і т.і.). Виходячи і з цього, необхідно порівнювати не індивідуальні, а узагальнювальні показники рівня розкриваємості. Абсолютне число розкритих злочинів в конкретному підрозділі також непридатне для такого порівняння, оскільки за інших рівних умов, як правило, цей показник буде тим вище, чим більше співробітників в даному підрозділі. Отже, лише розділивши загальну розкриваність по підрозділу на число співробітників і набувши середнього значення розкриваємості по кожному підрозділу, можна порівняти одержані величини і визначити, в якому підрозділі рівень розкриваємості злочинів вищий, а також більш ефективніша профілактична діяльність. Узагальнюючи існуючі у спеціальній літературі поняття, можна зробити висновок, що середньою величиною в статистиці називається узагальнювальний показник, який характеризує усереднене значення будь-якої ознаки сукупності (наприклад, злочинності, розкриття злочинів або кількість справ, що розслідуються) за визначений період на певній території.
Основною умовою правильного наукового використання середньої величини в статистиці є якісна однорідність сукупності, по якій обчислена середня. Тому перед численням середніх величин всі одиниці сукупності розчленовують на однорідні групи, по яких і обчислюють середні. Якщо не провести такого розчленовування, то в результаті можна дійти «огульної» середньої, яка абсолютно неправильно буде характеризувати спостережувану сукупність. Метод середніх величин невід’ємний від методу угрупувань, оскільки саме угрупування забезпечують якісну однорідність досліджуваних статистичних сукупностей.
Але тільки середніх показників недостатньо для оцінки тих або інших явищ. Середні показники порівнюють, згладжують індивідуальні особливості окремих одиниць сукупності і тим самим можуть затушовувати прояв негативних тенденцій.
Середні величини широко використовуються при вивченні соціально-економічних і соціально-правових процесів, що відображають результати діяльності держави, органів і установ, громадських структур (наприклад, середні темпи зростання і приросту об'єму злочинності або розкриваємості, підвищення ефективності системи профілактичних заходів тощо).
Статистична сукупність складається з множини одиниць, об'єктів або явищ однорідних в певному відношенні і одночасно відмінних за величиною ознак. Величина ознаки кожного об'єкта визначається як загальними для всіх одиниць сукупності, так і індивідуальними її особливостями.
Аналізуючи впорядковані ряди розподілу (ранжировані, інтервальні та ін.), можна помітити, що елементи статистичної сукупності явно концентруються навколо деяких центральних значень. Така концентрація окремих значень ознаки навколо деяких центральних значень, як плавило, має місце у всіх статистичних розподілах. Тенденцію окремих значень досліджуваної ознаки групуватися навколо центра розподілу частот називають центральною тенденцією. Для характеристики центральної тенденції розподілу застосовуються узагальнюючі показники, які отримали назву середніх величин.
Обчислюється середня величина у більшості випадків шляхом ділення загального обсягу ознаки на число одиниць, що володіють цією ознакою. Якщо, наприклад, взяти фонд місячної заробітної плати і кількість робітників, що працюють на підприємстві, то середню місячну заробітну плату можна визначити шляхом ділення фонду заробітної плати на кількість робітників.
Середні величини, які обчислюються як з абсолютних, так і з відносних величин, є показниками іменованими і виражаються в тих самих одиницях виміру, що і усереднювана ознака. Вони характеризують одним числом значення досліджуваної сукупності. В середніх величинах знаходить відображення об'єктивний і типовий рівень соціально-економічних явищ і процесів, що відбуваються в будь-якій країні.
У статистичній науці і практиці середні величини мають виключно велике значення. Метод середніх величин є одним з найважливіших статистичних методів, а середня величина - однією з основних категорій статистичної науки. Теорія середніх величин займає одне з центральних місць в теорії статистики. Середні величини є основою для розрахунку показників варіації, помилок вибірки, дисперсійного і кореляційного аналізу.
У випадках, виникнення необхідності надати характеристику сукупності значення якої періодично змінюється, користуються її середнім значенням.
В статистичній сукупності значення ознаки постійно змінюється, тобто варіює. Ця властивість статистичної сукупності, яка при її усередненні повинна бути залишатися незмінною, називається визначальною властивістю середньої по відношенню до досліджуваної ознаки. Інакше кажучи, середня величина замінюючи індивідуальні значення ознаки, не повинна змінювати загального обсягу явища, тобто обов'язкова така рівність: обсяг явища дорівнює добутку середньої величини на чисельність сукупності. Наприклад, якщо з трьох значень злочинності по регіонах (х - = 442; 540; 515) обчислена середня (442+540+515):3=498, то за визначальною властивістю середньою має бути дотримана така рівність: п ~ х = пх; тобто 3 Х 498 = 442+540+512; 1494=1494.
Головне значення середніх величин полягає в їх узагальнюючій функції, тобто заміні множини різних індивідуальних значень ознаки середньою величиною, яка характеризує всю сукупність явищ. Властивість середньої характеризувати не окремі одиниці, а виразити рівень ознаки з розрахунку на кожну одиницю сукупності є її відмінною спроможністю. Ця особливість робить середню узагальнюючим показником рівня варіюючої ознаки, тобто показником, який абстрагується від індивідуальних значень розміру ознаки у окремих одиниць сукупності. Але те, що середня є абстрактною, не позбавляє її наукового дослідження. Абстракція є необхідним ступенем усякого наукового дослідження. В середній величині, як у будь-якій абстракції, здійснюється діалектична єдність індивідуального і загального. Взаємозв'язок середніх і окремих значень усереднюваної ознаки служить вираженням діалектичного зв'язку індивідуального і загального.
Застосування середніх величин має базуватися на розумінні та взаємозв'язку діалектичних категорій загального і індивідуального, масового і одиничного.
Середня величина відображає те загальне, що складається в кожному окремому (одиничному) об'єкті. Завдяки цьому середня отримує велике значення для виявлення закономірностей, притаманних масовим суспільним явищам і не помітних в одиничних явищах.
У розвитку явищ необхідність поєднується з випадковістю. Тому середні величини пов’язані із законом великих чисел. Суть цього зв'язку полягає в тому, що при розрахунку середньої величини випадкові коливання, що мають різну спрямованість, через дію закону великих чисел взаємно урівноважуються, погашаються і у величині середньої чітко відображається основна закономірність, необхідність, вплив загальних умов, характерних для даної сукупності. В середній знаходить відображення типовий, реальний рівень досліджуваних явищ. Оцінка цих рівнів і зміна їх в часі і просторі - одне з головних завдань середніх величин. Так, через середні виявляється, наприклад, закономірність підвищення продуктивності праці, урожайності сільськогосподарських культур, продуктивності тварин. Отже, середні величини являють собою узагальнюючі показники, в яких знаходить своє відображення дія загальних умов, закономірність досліджуваного явища.
За допомогою середніх величин вивчають зміну явищ у часі і просторі, тенденції в їх розвитку, зв'язки і залежності між ознаками, ефективність різних форм організації виробництва, праці і технологій, впровадження науково-технічного прогресу, виявлення нового, прогресивного в розвитку тих чи інших соціально-економічних явищ і процесів.
Середні величини широко застосовуються в статистичному аналізі, оскільки саме в них знаходять своє виявлення закономірності і тенденції розвитку масових суспільних (правових) явищ, варіюючих як у часі, так і у просторі. Так, наприклад, існує закономірність між підвищенням ефективності в правоохоронній (заснованої на професіоналізмі) діяльності та зростанням показників у попередженні або розкритті злочинів.
Середня величина дає узагальнену характеристику досліджуваного явища тільки за однією ознакою, яка відображає одну з найважливіших його сторін. У зв'язку з цим для всебічного аналізу досліджуваного явища необхідно будувати систему середніх величин за рядом взаємопов'язаних і доповнюючих один одного суттєвих ознак.
Для того щоб середня величина відображала дійсно типове і закономірне в досліджуваних суспільних явищах, при її розрахунку необхідно дотримуватись таких умов.
Середню величину, як вже було зазначено вище, потрібно обчислювати тільки за якісно однорідною сукупністю. Тому безпосередньому обчисленню середніх має передувати статистичне групування, яке дає змогу розчленувати досліджувану сукупність на якісно однорідні групи. У зв'язку з цим науковою основою методу середніх величин є метод статистичних групувань.
Ознака, за якою обчислюється середня величина, має бути істотною. В іншому випадку буде отримана величина, що не відповідає середній між декількома явищами сукупності.
Розрахунок середньої величини має базуватися на охопленні всіх одиниць даного типу або досить великої сукупності об'єктів, щоб випадкові коливання взаємно зрівноважували один одного і проявлялася закономірність, типові і характерні розміри досліджуваної ознаки.
Загальною вимогою при розрахунку будь-якого виду середніх величин є збереження незмінним загального обсягу ознаки в сукупності, при заміні індивідуальних її значень середнім значенням (так звана визначальна властивість середньої).
У статистиці застосовуються різні види середніх величин: середня арифметична, середня гармонійна, середня геометрична.
Крім вищезазначених на практиці використовують ще й такі види середніх величин як: середня хронологічна, середня прогресивна, середня багатовимірна, середня ковзна, а також середні структурні: мода, медіана.
Будь-яку з вищезазначених середніх можна визначити як просту (коли значення варіант спостерігається один раз або однакову кількість разів) і як зважений, коли значення варіант повторюється декілька разів.
Уведемо такі позначення і поняття середніх:
х - середнє значення досліджуваної ознаки;
х - окремі значення усереднюваної ознаки (варіанти);
п - число одиниць досліджуваної сукупності;
/- частота повторень (вага) варіант;
W = xf- обсяг явищ.
Ознаку за якою знаходять середню називають усередненою ознакою. Величину ознаки кожної окремої одиниці сукупності називають варіантою, або значенням досліджуваної ознаки. Частоту повторень варіантів у сукупності (наприклад, загальній кількості вчинених злочинів) називають статистичною вагою.
Вибір того чи іншого виду середньої визначається цілями і завданнями дослідження і наявною інформацією.
Загальною умовою правильного обчислення усіх видів середніх є збереження незмінним загального обсягу варіюючої ознаки при заміні індивідуальних значень ознаками їхньої середньої. Так, середня арифметична застосовується тоді, коли обсяг варіюючої ознаки утворюється як сума окремих варіант; середня гармонічна - коли обсяг варіюючої ознаки утворюється як сума обернених значень окремих варіант; середня геометрична - коли обсяг варіюючої ознаки утворюється як добуток окремих варіант; середня квадратична - коли обсяг варіюючої ознаки утворюється як сума квадратів окремих варіант.
Розглянемо перелічені вище види середніх величин більш докладно.
Найбільш поширеним видом середніх величин в статистиці є середня арифметична, що є результатом ділення суми індивідуальних значень ознак на їх кількість. Середня арифметична величина буває простою і зваженою.
Середня арифметична проста являє собою частку від ділення суми індивідуальних значень ознаки на їх загальне число. її обчислюють за формулою
Середня арифметична проста застосовується в тих випадках, коли відомі дані про окремі значення ознаки та їх число в сукупності. В статистичній практиці вона застосовується, як правило, для розрахунку середніх рівнів ознак, наданих у вигляді абсолютних показників.
Для з'ясування методики розрахунку середньою арифметичною використовуємо наступні позначення:
X - арифметична ознака
X (X1, X2,... X3) - варіанти певної ознаки
n - число одиниць сукупності
 - середня величина ознаки
- середня величина ознаки
Залежно від початкових даних середня арифметична може бути розрахована двома способами:
1. Якщо дані статистичного спостереження не згруповані, або згруповані варіанти мають однакові частоти, то розраховується середня арифметична проста:

Допустимо, що кількість правопорушень по 10 населеним пунктам регіону за звітний період склало: 3100, 3600, 4500, 4900, 5300, 5400, 5600, 5700, 5900, 6000. Стан злочинності одного населеного пункту саме по собі не може дати уявлення про її рівень по всьому регіону. Для цього треба визначити середній рівень злочинності. Його в даному прикладі можна визначити так: підсумовуємо стан злочинності по всіх населених пунктах і одержаний підсумок розділимо на число населених пунктів в обстежуваному регіоні. Це дасть наступне рівняння:
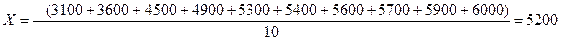
Тобто середньорічний рівень злочинності по регіону складає 5200 злочинів. Це проста середня арифметична величина. Простою вона називається тому, що обчислюється простим підсумовуванням індивідуальних значень ознаки і діленням цієї суми на число значень. В статистичній практиці вона застосовується, як правило, для розрахунку середніх рівнів ознак наданих у вигляді абсолютних показників.
2. Якщо згруповані варіанти в даних мають різні частини, то розраховується середня арифметична зважена:

 - чисельність (частоти) варіантів
- чисельність (частоти) варіантів
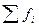 - сума частот
- сума частот
Для прикладу середньої зваженої візьмемо дані про стан злочинності в різних населених пунктах, у табл. 2.1
Таблиця 2. 1
Стан злочинності по населених пунктах регіону (дані умовні)
| Населені пункти регіону | |||||
| Пункти | |||||
| Назва пунктів | Пункт А. | Пункт Б. | Пункт С. | Пункт Д. | Пункт Е. |
| Кількість вчинених злочинів | |||||
| Кількість населених пунктів, в яких повторюються (співпадає) кількість злочинних проявів |
У даному прикладі тільки в двох населених пунктах стан злочинності за даний період склав 2700 епізодів, в чотирьох - 2000 і т.і., тобто кожен варіант повторюється неоднакове число разів. Тому при обчисленні середнього рівня злочинності не можна користуватися формулою середньої арифметичної простій. Щоб визначити рівень злочинності по досліджуваних населених пунктах, спочатку треба визначити загальний стан злочинності для всіх населених пунктів. Для цього помножують по кожній групі кількість злочинів на число населених пунктів і одержані дані підсумовують. Середній рівень злочинності по всій сукупності населених пунктів визначається діленням одержаної суми на число населених пунктів. У нашому прикладі частотами є 2, 3, 4, 5, 6. Вони показують, що кількість злочинів, що дорівнює 2700 фактам, зустрічається в 2 населених пунктах, тобто 2 рази, 2000 - 4 рази тощо. Частоти ще називають вагами середньої величини, звідси і відбувається назва середньої зваженої.
Позначивши умовно частоти літерою Х, розрахунок середній арифметичній зваженій можна виразити наступною формулою:

 - середнє значення досліджуваної ознаки (варіанти)
- середнє значення досліджуваної ознаки (варіанти)
Xf – обсяг явищ
f – частота повторень варіант
Таким чином, при численні середньої арифметичної зваженої величини необхідно всі значення варіант помножити на їхню частоту, одержані рівняння підсумувати і цю суму розділити на суму частот, тобто загальний обсяг сукупності.
Частоти f називають вагою, а множення варіантів Х на частоти - зважуванням. Замість частот можливе застосування часток d. Тоді форма середньоарифметичної зваженої буде виглядати таким чином:
 = x1d1+x2d2+x3d3+ … +xmdm=
= x1d1+x2d2+x3d3+ … +xmdm= 
Середня арифметична має певні властивості, найсуттєвішими з яких є:
1) сума відхилень усіх значень правової ознаки від середнього її значення дорівнює 0;
2) добуток середнього значення дорівнює сумі індивідуальних значень ознаки, тобто загальному обсягу цієї ознаки;
3) сума квадратів відхилень кожного значень ознаки від середньої величини завжди менша за будь-яку величину[15].
Якщо частоти різні, то розрахунок середньої величини роблять за середньою арифметичною зваженою[16].
Середня називається арифметичною зваженою, тому що визначається з урахуванням питомої ваги окремих значень ознаки загальної сукупності (х f)
Розглядаючи формули середньої арифметичної зваженої можна помітити, що вона майже не має відміни від простої середньої арифметичної. В ній підсумовування f (кількість) разів одного і того ж самого варіанта (х) замінюють множенням його на число повторень (частоту - f).
Покажемо це на прикладі (таб. 2.1)
Таблиця 2.2
Не нашли, что искали? Воспользуйтесь поиском: