
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Результаты выборочного обследования доходов населения
| Район | Численность населения, чел. | Обследовано, чел. | Доход в расчете на 1 человека | |
| средняя, тыс. руб. | дисперсия | |||
| I II III | 2,9 2,5 2,7 | 1,3 1,1 1,6 |
Необходимо определить границы среднедушевых доходов населения по области в целом при уровне вероятности 0,997.
Решение. Рассчитаем среднюю из внутригрупповых дисперсий:

Средняя и предельная ошибки выборки:


Рассчитаем выборочную среднюю:
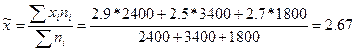 тыс.руб.
тыс.руб.
В результате проведенных расчетов с вероятностью 0,997 можно сделать вывод, что среднедушевые доходы жителей данной области находятся в следующих границах (тыс. руб.):

При определении необходимого объема типической выборки учитывается средняя из внутригрупповых дисперсий:
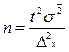 (повторный отбор);
(повторный отбор);
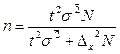 (безповторный отбор).
(безповторный отбор).
Полученное значение общего объема выборки необходимо распределить по типическим группам пропорционально их численности, чтобы определить, какое количество единиц следует отобрать из каждой группы:

где Ni – объем i -и группы;
n, - объем выборки из /-и группы.
Серийная выборка. Эта выборка используется в тех случаях, когда единицы изучаемой совокупности объединены в небольшие равновеликие группы или серии. Единицей отбора в этом случае является серия. Серии отбираются с использованием собственно-случайной либо механической выборки, а внутри отобранных серий обследуются все без исключения единицы.
В основе расчета средней ошибки серийной выборки лежит межгрупповая дисперсия:
 (повторный отбор);
(повторный отбор);
 (бесповторный отбор),
(бесповторный отбор),
где xi - число отобранных i - серий;
R - общее число серий.
Межгрупповую дисперсию при равновеликих группах вычисляют следующим образом:
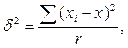
где хi – средняя i-и серии;
х – общая средняя по всей выборочной совокупности.
Пример
В целях контроля качества комплектующих из партии изделий, упакованных в 50 ящиков по 20 изделий в каждом, была произведена 10%-ная серийная выборка. По попавшим в выборку ящикам среднее отклонение параметров изделия от нормы соответственно составило 9 мм, 11, 12, 8 и 14 мм. С вероятностью 0,954 определите среднее отклонение параметров по всей партии в целом.
Решение. Выборочная средняя:
 мм.
мм.
Величина межгрупповой дисперсии:

С учетом установленной вероятности Р = 0,954 (t = 2) предельная ошибка выборки составит:
 мм.
мм.
Произведенные расчеты позволяют заключить, что среднее отклонение параметров всех изделий от нормы находится в следующих границах:

Для определения необходимого объема серийной выборки при заданной предельной ошибке используются следующие формулы:
 (повторный отбор);
(повторный отбор);
 (безповторный отбор).
(безповторный отбор).
Не нашли, что искали? Воспользуйтесь поиском: