
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сложение взаимно перпендикулярных колебаний
Рис.1
5.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты , происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем
 (145.1)
(145.1)
где — разность фаз обоих колебаний, А и В — амплитуды складываемых колебаний. Уравнение траектории результирующего колебания находится исключением из выражений (145.1) параметра t. Записывая складываемые колебания в виде

и заменяя во втором уравнении cos t на х/А и sin t на  , получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно:
, получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно:
 (145.2)
(145.2)
Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз . Рассмотрим некоторые частные случаи, представляющие физический интерес:
1) = m (m =0, ±1, ±2,...). В данном случае эллипс вырождается в отрезок прямой
 (145.3)
(145.3)
где знак плюс соответствует нулю и четным значениям т (рис. 205, а), а знак минус — нечетным значениям т (рис. 205, б). Результирующее колебание является гармоническим колебанием с частотой и амплитудой 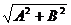 , совершающимся вдоль прямой (145.3), составляющей с осью х угол = arctg
, совершающимся вдоль прямой (145.3), составляющей с осью х угол = arctg  . В данном случае имеем дело с линейно поляризованными колебаниями;
. В данном случае имеем дело с линейно поляризованными колебаниями;
2) = (2 m+ 1)  (m =0, ± 1, ±2,...). В данном случае уравнение примет вид
(m =0, ± 1, ±2,...). В данном случае уравнение примет вид
 (145.4)
(145.4)
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 206). Кроме того, если А=В, то эллипс (145.4) вырождается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.

Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. * Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 207 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху; разность фаз принимается равной ).
6. Гармонические колебания в электрическом контуре
Рассмотрим замкнутую электрическую цепь, состоящую из конденсатора емкостью С и катушки индуктивностью L, без активного сопротивления. Такая цепь называется идеальным колебательным контуром.
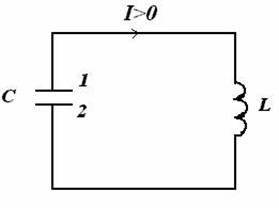
Если конденсатор был предварительно заряжен, то после замыкания цепи в ней пойдет ток. Закон Ома для участка цепи 1 - L - 2 запишется следующим образом:
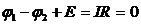
где Е - э.д.с. самоиндукции.
Если в этом уравнении сделать подстановки:
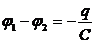

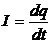
то придем к следующему уравнению относительно заряда q:

Сравнивая его с уравнением свободных гармонических колебаний, видим, что полученное уравнение также является уравнением свободных гармонических колебаний заряда на обкладках конденсатора с циклической частотой:

Колебания заряда в контуре происходят по закону:

сравните с уравнением колебаний маятника,
|
а колебания тока -

В этих формулах: q0 - амплитуда заряда, I0 - амплитуда тока,

Ток в контуре опережает заряд конденсатора по фазе на /2.
Разность потенциалов на обкладках конденсатора также меняется по синусоидальному закону (синхронно с колебаниями заряда):

Амплитуду тока можно выразить через амплитуду напряжения:

В таком виде формула напоминает закон Ома, а размерность знаменателя соответствует размерности сопротивления. Поэтому величину, стоящую в знаменателе называют волновым сопротивлением контура. Это сопротивление не следует путать с активным сопротивлением R (которого в нашем идеализированном контуре нет). Сопротивление изменяющемуся току оказывают не столкновения носителей заряда (электронов) в проводнике с ионами кристаллической решетки с безвозвратной потерей электромагнитной энергии, а э.д.с. самоиндукции в катушке в соответствии с законом
| Фарадея.
|
7.3.1. Механические затухающие колебания
Механическая система: пружинный маятник с учетом сил трения.
Силы, действующие на маятник:
Упругая сила.  , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
, где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления):  . Знак "минус" показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
. Знак "минус" показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:

Закон движения пружинного маятника – это второй закон Ньютона:
m a = F упр. + F сопр.
Учитывая, что 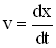 и
и 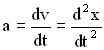 , запишем второй закон Ньютона в виде:
, запишем второй закон Ньютона в виде:
 .
.
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
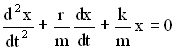
Обозначим  , где β – коэффициент затухания,
, где β – коэффициент затухания,  , где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
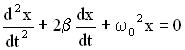 .
.
Это линейное дифференциальное уравнение второго порядка.
Уравнение затухающих колебаний есть решение такого дифференциального уравнения:
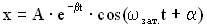
 .
.
Период затухающих колебаний:
 .
.
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
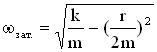 ,
,  .
.
Графики зависимости смещения от времени 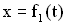 и амплитуды от времени
и амплитуды от времени  представлены на Рисунках 3.1 и 3.2.
представлены на Рисунках 3.1 и 3.2.

Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.
| 8Свободные затухающие электрические колебания |  
|
Всякий реальный контур обладает активным сопротивлением (рис. 4.3). Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего колебания затухают.
 Рис. 4.3
По второму закону Кирхгофа:
Рис. 4.3
По второму закону Кирхгофа:
Обозначим
При
где
Рис. 4.4 На рис. 4.4 показан вид затухающих колебаний заряда q и силы тока I. Если сравнить электрические затухающие колебания с механическими (рис. 3.1), то хорошо видны общие закономерности этих явлений: колебаниям q соответствует x – смещение маятника из положения равновесия, силе тока I – скорость υ. |
9,ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, происходящие под действием внешней переменной силы (вынуждающей силы).
Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.
Рассмотрим вынужденные колебания на примере реального (с трением) пружинного маятника. Будем отталкиваться от уравнения движения (второй закон Ньютона), которое мы написали для затухающих колебаний. При наличии дополнительной вынуждающей силы F (t) необходимо дописать ее в правую часть уравнения. В каноническом виде дифференциальное уравнение вынужденных механических колебаний имеет вид:

Для пружинного маятника:
 и
и 
Для того, чтобы возникли периодические колебания, вынуждающая сила сама должна быть периодической. Пусть  (писать здесь начальную фазу смысла нет, поскольку нас будут интересовать только установившиеся вынужденные колебания, то есть "забывшие" свое начало). - частота вынуждающей силы. Для нахождения уравнения установившихся колебаний необходимо найти решение дифференциального уравнения:
(писать здесь начальную фазу смысла нет, поскольку нас будут интересовать только установившиеся вынужденные колебания, то есть "забывшие" свое начало). - частота вынуждающей силы. Для нахождения уравнения установившихся колебаний необходимо найти решение дифференциального уравнения:
 при
при  .
.
Общее решение этого неоднородного дифференциального уравнения представляет собой, как известно из теории дифференциальных уравнений, сумму общего решения однородного уравнения и любого частного решения неоднородного. Общее решение однородного уравнения нам известно, это - уравнение затухающих колебаний. Оно нас не интересует, так как при  оно исчезает. В качестве частного решения неоднородного уравнения выберем очевидное - мы знаем, что вынужденные установившиеся колебания совершаются с частотой вынуждающей силы. Поэтому нашим искомым решением будет являться:
оно исчезает. В качестве частного решения неоднородного уравнения выберем очевидное - мы знаем, что вынужденные установившиеся колебания совершаются с частотой вынуждающей силы. Поэтому нашим искомым решением будет являться:
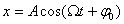
где А - амплитуда вынужденных колебаний, ۪ - сдвиг фаз между смещением и приложенной силой.
Получившиеся колебания подчиняются закону синуса (или косинуса), то есть являются синусоидальными или гармоническими. Но это не свободные колебания в системе без трения; здесь вынуждающая сила постоянно поставляет энергию в систему, в точности компенсирующую потери на преодоление сил трения.
Необходимо теперь найти амплитуду вынужденных колебаний и сдвиг фаз. Для этого необходимо подставить выражение для х в дифференциальное уравнение вынужденных колебаний. Обратите внимание, что необходимо найти два неизвестных из одного уравнения. Это возможно, если в процессе вычислений воспользоваться дополнительным (очевидным в процессе выкладок) условием. Попытайтесь проделать это.
Для амплитуды и сдвига фаз получаются следующие выражения:
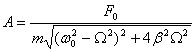

здесь - частота свободных (незатухающих) колебаний маятника; - коэффициент затухания.
Обратите внимание, что амплитуда вынужденных колебаний зависит от соотношения частоты вынуждающей силы и собственной частоты маятника. Максимальное значение амплитуды получается, если 
Частота  называется резонансной частотой, а достижение максимума амплитуды колебаний при изменении частоты называется явлением резонанса. График зависимости А () носит название резонансной кривой. Обратите внимание, что резонансная частота механических колебаний зависит от коэффициента затухания (а с ним и от коэффициента силы трения). Если силы трения отсутствуют, амплитуда колебаний стремится к бесконечности.
называется резонансной частотой, а достижение максимума амплитуды колебаний при изменении частоты называется явлением резонанса. График зависимости А () носит название резонансной кривой. Обратите внимание, что резонансная частота механических колебаний зависит от коэффициента затухания (а с ним и от коэффициента силы трения). Если силы трения отсутствуют, амплитуда колебаний стремится к бесконечности.

Помимо поведения амплитуды при резонансной частоте рассмотрим ещё два предельных случая:  и
и 
В первом мы получим обычное статическое смещение маятника под действием постоянной силы F0 (статическое растяжение пружины):

Во втором случае амплитуда равна нулю: инерция маятника не может успевать реагировать на бесконечную частоту.
Зависимость сдвига фаз от соотношения частот представлена на рисунке. Сдвиг фаз между смещением и вынуждающей силой обусловлен инерцией маятника.

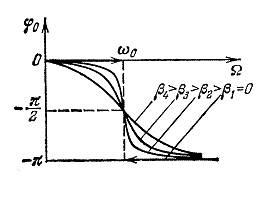
Резона́нс (— явление, при которомамплитуда вынужденных колебаний имеет максимум при некотором значении частотывынуждающей силы. Часто это значение близко к частоте собственных колебаний, фактически может совпадать, но это не всегда так и не является причиной резонанса.
В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемойдобротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
10.
Не нашли, что искали? Воспользуйтесь поиском:

 .
.
 , или
, или 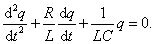
 – коэффициент затухания и, учитывая, что собственная частота контура
– коэффициент затухания и, учитывая, что собственная частота контура  , получим уравнение затухающих колебаний в контуре с R, L и С:
, получим уравнение затухающих колебаний в контуре с R, L и С: .
.
 , т.е.
, т.е.  , решение этого уравнения имеет вид:
, решение этого уравнения имеет вид:
 – частота затухающих колебаний контура, или
– частота затухающих колебаний контура, или  , т.е.
, т.е.  .
.