
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Векторы на плоскости (R2), в пространстве R3 и в n-мерном пространстве Rn.
МАТРИЦЫ
1. Найти произведение элементов главной диагонали матрицы.
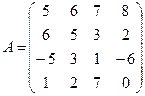
А) 25 Б) 0 В) 5 Г) 48
2. Найти матрицу 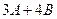 , если
, если  и
и 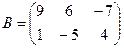 .
.
А) 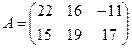 ; Б)
; Б)  ; В)
; В) 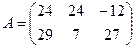 ; Г)
; Г) 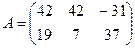 .
.
3. Укажите размерность матрицы, которую можно умножить как слева, так и справа на матрицу 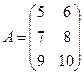
А) 3х2 Б) 2х3 В) 3х3 Г) 3х1
4. Найти элемент с23 матрицы С=АхВ, если 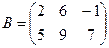 и
и 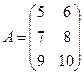 .
.
А) 49 Б) 94 В) 48 Г) 84
5. Решением уравнения ХА= В, где А,В – квадратные матрицы одного и того же порядка, причем А – невырожденная матрица, является матрица Х
А) Х=А-1В Б) Х=АВ-1 В) Х=В-1А Г) Х=ВА-1
6. Даны матрицы  . Могут ли быть перемножены матрицы:
. Могут ли быть перемножены матрицы:
А) В,А и С,В? Б) В,С и А,В? В) В,А и А,С? Г) С,А и В,С?
7. Укажите матрицу, ранг которой равен двум.
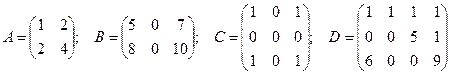
А) А Б) В В) С Г) D
8) Даны матрицы 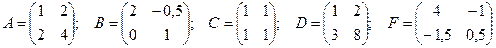 .
.
Обратной к D является:
А) А Б) В В) С Г) F
9) Дана матрица 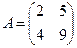 . Обратной к ней является:
. Обратной к ней является:
А) 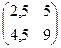 Б)
Б) 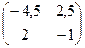 В)
В)  Г)
Г) 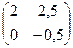
ОПРЕДЕЛИТЕЛИ
10. Как изменится определитель матрицы третьего порядка, если все его элементы умножить на число 3?
А) Увеличится в 3 раза;
Б) Не изменится;
В) Увеличится в 27 раз;
Г) Увеличится в 9 раз.
11. Какому числу равно алгебраическое дополнение элемента a32 определителя:
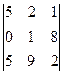 ?
?
А) 40 Б) 4 В) -40 Г) 24
12. Вычислите определитель произведения А˟В, если 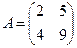 и
и 
А) 34Б) 35В) 36Г)37
13. Вычислить определитель 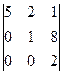
А) 8Б) 7В) 9Г) 6
14. Как изменится определитель, если из его первой строки вычесть третью, умноженную на 2?
А) Изменит свой знак;
Б) Не изменится;
В) Станет равным нулю;
Г) Увеличится в - 2 раза.
15. Определитель матрицы системы 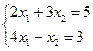 равен:
равен:
А) -18Б) -14В) 19Г) 16
16. Найдите значение определителя матрицы, обратной к данной матрице А:
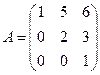
А) 2Б) -4В) -2Г) 4
17. Существует ли определитель матрицы 
А) Да, и равен нулю;
Б) Нет;
В) Да, и равен -7;
Г) Да, и равен -8.
18. Вычислить элемент матрицы с22, обратной к матрице 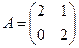
А) 0,5Б) 0,6В) 0,7Г) 0,8
Векторы на плоскости (R2), в пространстве R3 и в n-мерном пространстве Rn.
19. Даны векторы  . Какие из них являются коллинеарными?
. Какие из них являются коллинеарными?
А)  Б)
Б)  В)
В)  Г)
Г) 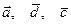
20. Скалярное произведение двух векторов 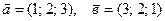 равно
равно
А) 13Б) 10В) 12Г) вектору 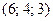
21. Даны векторы  . Какие из них ортогональны?
. Какие из них ортогональны?
А) 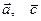 Б)
Б) 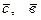 В)
В) 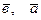 Г) нет ортогональных векторов.
Г) нет ортогональных векторов.
22. Даны векторы 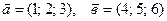 . Найти линейную комбинацию
. Найти линейную комбинацию 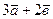 .
.
А) 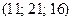 Б)
Б)  В)
В) 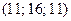 Г)
Г) 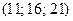
23. Ранг системы векторов 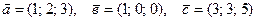 равен:
равен:
А) 2Б) 3В) 4Г) 1
24. Даны векторы 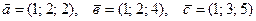 . Базисом данной системы является
. Базисом данной системы является
А) Любые два вектора;
Б) 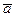 ;
;
В)  ;
;
Г) 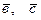 .
.
25. Векторы 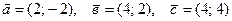 заданы в единичном ортонормированном базисе пространства R2. Вектор
заданы в единичном ортонормированном базисе пространства R2. Вектор 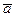 в базисе
в базисе 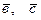 имеет координаты:
имеет координаты:
А)  Б)
Б)  В)
В) 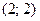 Г)
Г) 
26. Длина вектора 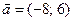 равна
равна
А) 5Б) 4В) 40Г) 10
27. Угол между векторами  равен
равен
А) 00Б) 900В) 1800Г) 600
28. Даны точки А(3;8) и В(5;5). Найти координаты вектора 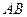 .
.
А) 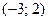 Б)
Б) 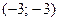 В)
В)  Г)
Г) 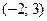
Не нашли, что искали? Воспользуйтесь поиском: