
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ықтималдықтар теориясы
Зіндік жұмыс
1. Екіойын сүйегі лақтырылды. Түскен ұпайдың қосындысы: а)  ға тең; ә)
ға тең; ә)  дан кем емес; б)
дан кем емес; б)  дан кем рет ықтималдықтарын табу керек.
дан кем рет ықтималдықтарын табу керек.

| 
| 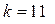
| 
| 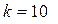
| |||||

| 
| 
| 
| 
| |||||
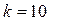
| 
| 
| 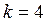
| 
| |||||

| 
| 
| 
| 
| |||||

| 
| 
| 
| 
| |||||
| 
| 
| 
| 
|
2. 25 бұйым бар. Оның  бірінші сортты бұйымдар. Бақылау үшін кез келген 8 бұйым алынды. Оның ішінде
бірінші сортты бұйымдар. Бақылау үшін кез келген 8 бұйым алынды. Оның ішінде 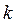 бірінші сортты бұйымдар болуының ықтималдығын табу керек.
бірінші сортты бұйымдар болуының ықтималдығын табу керек.
| № | 
| 
| № | 
| 
| № | 
| 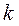
| № | 
| 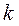
| № | 
| 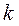
|
3. Үш бригада белгілі бір жұмысты істейді. Осы жұмысты орындау ықтималдығы бірінші бригада үшін -  екінші бригада үшін –
екінші бригада үшін –  үшінші бригада үшін -
үшінші бригада үшін -  -ке тең. Осы жұмысты: а) үш бригаданың орындау; ә) тек екі бригаданың орындау; б) тек бір бригаданың орындау; в) үш бригаданың да орындамауының; г) ең болмаса бір бригаданың орындау ықтималдығын табу керек.
-ке тең. Осы жұмысты: а) үш бригаданың орындау; ә) тек екі бригаданың орындау; б) тек бір бригаданың орындау; в) үш бригаданың да орындамауының; г) ең болмаса бір бригаданың орындау ықтималдығын табу керек.
| № | 
| 
| 
| № | 
| 
| 
|
| 0,84 | 0,82 | 0,88 | 0,83 | 0,80 | 0,77 | ||
| 0,78 | 0,80 | 0,84 | 0,85 | 0,82 | 0,79 | ||
| 0,92 | 0,88 | 0,90 | 0,87 | 0,90 | 0,93 | ||
| 0,90 | 0,92 | 0,94 | 0,89 | 0,86 | 0,83 | ||
| 0,86 | 0,88 | 0,94 | 0,91 | 0,87 | 0,83 | ||
| 0,82 | 0,80 | 0,78 | 0,93 | 0,89 | 0,86 | ||
| 0,80 | 0,84 | 0,86 | 0,84 | 0,79 | 0,75 | ||
| 0,76 | 0,73 | 0,70 | 0,83 | 0,79 | 0,77 | ||
| 0,72 | 0,69 | 0,66 | 0,77 | 0,74 | 0,71 | ||
| 0,74 | 0,71 | 0,68 | 0,70 | 0,80 | 0,70 | ||
| 0,76 | 0,79 | 0,82 | 0,70 | 0,75 | 0,65 | ||
| 0,77 | 0,80 | 0,83 | 0,77 | 0,73 | 0,81 | ||
| 0,79 | 0,82 | 0,85 | 0,71 | 0,75 | 0,79 | ||
| 0,81 | 0,84 | 0,87 | 0,73 | 0,78 | 0,83 | ||
| 0,83 | 0,86 | 0,89 | 0,75 | 0,81 | 0,84 |
4. Болттар дайындайтын фабрикада барлық бұйымдардың  -ын бірінші станокта, ал қалғанын екінші станокта шығарады. Бұл станоктарда шығатын болттардың сәйкесінше
-ын бірінші станокта, ал қалғанын екінші станокта шығарады. Бұл станоктарда шығатын болттардың сәйкесінше  ,
, 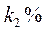 -ы жарамсыз болсын. Кездейсоқ алынған:
-ы жарамсыз болсын. Кездейсоқ алынған:
а) болттың жарамсыз;
ә) жарамсыз болт  ші машина жасағандығының ықтималдықтарын табу керек.
ші машина жасағандығының ықтималдықтарын табу керек.
| № | 
| 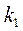
| 
| 
| № | 
| 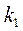
| 
| 
| № | 
| 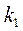
| 
| 
|
5. Цехта 7 мотор бар. Әрбір мотордың жұмыс істеу ықтималдығы р -ға тең. Төмендегі берілген оқиғалардың ықтималдықтарын табу керек:
а) барлық моторлар жұмыс жасайды; ә) барлық моторлар жұмыс істемейді; б) тек 3 мотор жұмыс істейді; в) 3-тен кем мотор жұмыс істейді; г) 3-тен кем емес мотор жұмыс істейді; ғ) 3-тен артық емес мотор жұмыс істейді; д) 3-тен артық мотор жұмыс істейді; е) ең болмаса бір мотор жұмыс істейді.
| № | 
| № | 
| № | 
| № | 
| № | 
|
| 0,75 | 0,71 | 0,65 | 0,81 | 0,92 | |||||
| 0,76 | 0,72 | 0,66 | 0,82 | 0,93 | |||||
| 0,77 | 0,83 | 0,67 | 0,73 | 0,87 | |||||
| 0,78 | 0,84 | 0,68 | 0,74 | 0,88 | |||||
| 0,69 | 0,85 | 0,79 | 0,95 | 0,94 | |||||
| 0,70 | 0,86 | 0,80 | 0,91 | 0,95 |
6. Әр п тәуелсіз тәжірибе нәтижесінде А оқиғасының пайда болу ықтималдығы р -ға тең. Осы сынау кезінде А оқиғасының
а) m рет; ә) m 1 -ден кем емес және m 2-ден артық емес пайда болу ықтималдығын табу керек.
| № | п | р | m | m 1 | m 2 | № | п | р | m | m 1 | m 2 |
| 0,60 | 0,60 | ||||||||||
| 0,80 | 0,80 | ||||||||||
| 0,90 | 0,960 | ||||||||||
| 0,40 | 0,4 | ||||||||||
| 0,75 | 0,75 | ||||||||||
| 0,36 | 0,36 | ||||||||||
| 0,50 | 0,50 | ||||||||||
| 0,2 | 0,20 | ||||||||||
| 0,25 | 0,25 | ||||||||||
| 0,64 | 0,64 | ||||||||||
| 0,75 | 0,75 | ||||||||||
| 0,60 | 0,90 | ||||||||||
| 0,90 | 0,64 | ||||||||||
| 0,20 | 0,80 | ||||||||||
| 0,40 | 0,40 |
7. Математикалық үміті  және дисперсиясы
және дисперсиясы  ықтималдығы
ықтималдығы  тең болатын Х дискретті кездейсоқ шамасының
тең болатын Х дискретті кездейсоқ шамасының  екі мән қабылдайды, мұндағы
екі мән қабылдайды, мұндағы  Кездейсоқ шаманың үлестірім заңын жазу керек.
Кездейсоқ шаманың үлестірім заңын жазу керек.
| № | 
| 
| 
| № | 
| 
| 
|
| 3,1 | 0,09 | 0,9 | 5,8 | 0,36 | 0,1 | ||
| 3,2 | 0,16 | 0,8 | 1,7 | 0,09 | 0,1 | ||
| 3,3 | 0,21 | 0,7 | 2,6 | 0,24 | 0,4 | ||
| 2,8 | 0,96 | 0,6 | 3,2 | 2,16 | 0,6 | ||
| 3,5 | 0,25 | 0,5 | 3,4 | 0,64 | 0,8 | ||
| 3,6 | 0,24 | 0,4 | 3,1 | 0,09 | 0,9 | ||
| 3,7 | 0,21 | 0,3 | 2,3 | 0,21 | 0,7 | ||
| 3,8 | 0,16 | 0,2 | 2,4 | 0,24 | 0,6 | ||
| 3,9 | 0,09 | 0,1 | 2,2 | 0,16 | 0,8 | ||
| 2,2 | 0,36 | 0,9 | 2,5 | 0,25 | 0,5 | ||
| 1,8 | 0,16 | 0,2 | 3,3 | 0,81 | 0,9 | ||
| 1,4 | 0,24 | 0,6 | 4,8 | 0,16 | 0,2 | ||
| 2,6 | 0,64 | 0,2 | 4,6 | 0,24 | 0,4 | ||
| 2,7 | 0,21 | 0,3 | 4,7 | 0,21 | 0,3 | ||
| 4,1 | 0,21 | 0,9 | 4,5 | 0,25 | 0,5 |
8. Х кездейсоқ шамасының  интегралдық функциясы берілген. f(x) дифференциалдық функциясын, М(Х) математикалық үмітін, D(X) дисперсиясын тауып, Х кездейсоқ шаманың мәндері
интегралдық функциясы берілген. f(x) дифференциалдық функциясын, М(Х) математикалық үмітін, D(X) дисперсиясын тауып, Х кездейсоқ шаманың мәндері
| № | 
| 
| 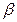
|

| -0,5 | 2,5 | |

| -0,5 | ||

| -0,5 | 2,5 | |

| 0,5 | 1,5 | |

| |||

| 0,5 | 2,5 | |

| -0,5 | 2,5 | |

| -1 | 1,5 | |

| -0,5 | 2,5 | |

| -0,5 | 2,5 | |

| -1,5 | 0,5 | |

| 0,5 | 2,5 | |

| -0,5 | 1,5 | |

| 0,5 | 3,5 | |

| 1,5 | 3,5 | |

| 0,1 | 0,5 | |

| 0,15 | 0,35 | |

| -0,5 | 0,1 | |

| -0,5 | 0,1 | |

| 0,08 | 0,12 | |
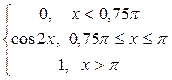
| 
| 
| |

| 
| 
| |

| 0,2 | 2,5 | |

| -4 | ||

| -1 | 1,5 | |

| 0,5 | 2,5 | |

| -0,2 | 0,2 | |

| 2,2 | 3,8 | |

| 
| ||

| -0,5 | 2,5 |
Тапсырмаларды шығару жолы
1. Екіойын сүйегі лақтырылды. Түскен ұпайдың қосындысы: а) 5-ке тең; ә) 5-тен кем емес; б) 5-тен кем рет ықтималдықтарын табу керек.
Шешуі. а) Барлық  элементар оқиғалар кеңістігін жазайық.
элементар оқиғалар кеңістігін жазайық.
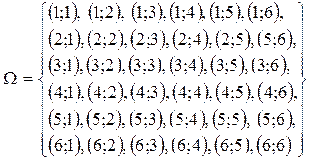
Түскен ұпайдың қосындысы 5-ке тең болуын  оқиғасы арқылы белгілейік.
оқиғасы арқылы белгілейік.  оқиғасына қолайлы болатын элементар оқиғаларын жазайық:
оқиғасына қолайлы болатын элементар оқиғаларын жазайық:
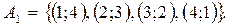
 оқиғасының ықтималдығының классикалық анықтамасы бойынша
оқиғасының ықтималдығының классикалық анықтамасы бойынша
 мұндағы п - барлық элементар оқиғалардың саны (п =36,
мұндағы п - барлық элементар оқиғалардың саны (п =36,  кеңістігін қара); т -
кеңістігін қара); т -  оқиғасының пайда болуына ықпал ететін оқиғалар саны (т= 4). Осыдан
оқиғасының пайда болуына ықпал ететін оқиғалар саны (т= 4). Осыдан
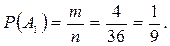
ә) Түскен ұпайдың қосындысы 5-тен кем емес болуын  оқиғасы арқылы белгілейік, онда
оқиғасы арқылы белгілейік, онда

 оқиғасының пайда болуына ықпал ететін оқиғалар саны т= 30-ге тең. Осыдан
оқиғасының пайда болуына ықпал ететін оқиғалар саны т= 30-ге тең. Осыдан 
б) Түскен ұпайдың қосындысы 5-тен кем болуын  оқиғасы арқылы белгілейік, онда
оқиғасы арқылы белгілейік, онда 
 оқиғасының пайда болуына ықпал ететін оқиғалар саны т= 6-ге тең. Осыдан
оқиғасының пайда болуына ықпал ететін оқиғалар саны т= 6-ге тең. Осыдан 
2. Үш сортты 25 бұйым бар. Оның 9-ы бірінші сортты бұйымдар. Бақылау үшін кез келген 8 бұйым алынды. Оның 5-і бірінші сортты бұйымдар болуының ықтималдығын табу керек.
Шешуі. А оқиғасы – «алынған 8 бұйымның 5-і бірінші сортты бұйымдар». А оқиғасының ықтималдығын келесі формуламен табамыз

Есептің берілгені бойынша N =25, т =8, n =9, k =5, сонда

3. Үш бригада белгілі бір жұмысты істейді. Осы жұмысты орындау ықтималдығы бірінші бригада үшін - 0,8; екінші бригада үшін – 0,7; үшінші бригада үшін - 0,9-ге тең. Осы жұмысты: а) үш бригаданың орындау; ә) тек екі бригаданың орындау; б) тек бір бригаданың орындау; в) үш бригаданың да орындамауының; г) ең болмаса бір бригаданың орындау ықтималдығын тап.
Шешуі. А1 оқиғасы – «жұмысты бірінші бригаданың орындауы»,
А2 оқиғасы – «жұмысты екінші бригаданың орындауы»,
А3 оқиғасы – «жұмысты үшінші бригаданың орындауы».

Онда осы жұмысты бригадаларының орындамауының ықтималдықтары сәйкесіше 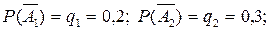
 .
.
а) В1 оқиғасы– «жұмысты үш бригаданың орындауы», онда 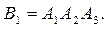 Осыдан
Осыдан 
ә) В2 оқиғасы – «жұмысты тек екі бригаданың орындауы». Онда 
Осыдан


б) В3 оқиғасы – «жұмысты тек бір бригаданың орындауы». Онда  Осыдан
Осыдан

в) В4 оқиғасы – «жұмысты үш бригаданың да орындамауы». Онда  Осыдан
Осыдан 
г) В5 оқиғасы – «жұмысты ең болмаса бір бригаданың орындауы». Онда В5 оқиғасы мен В4 оқиғасы толық топ құрайды. Осыдан

4. Болттар дайындайтын фабрикада барлық бұйымдардың 19%-ын бірінші станокта, ал қалғаны екінші станокта шығарады. Бұл станоктарда шығатын болттардың сәйкесінше 6%, 8%-ы жарамсыз болсын. Кездейсоқ алынған: а) болттың жарамсыз; ә) жарамсыз болт екінші машина жасағандығының ықтималдықтарын табу керек.
Шешуі.а) А1 оқиғасы – «кездейсоқ алынған болттың жарамсыз болуы».
В1 оқиғасы – «кездейсоқ алынған болттың бірінші станокта шығарады»,
В2 оқиғасы – «кездейсоқ алынған болттың екінші станокта шығарады». Онда 
Ал шартты ықтималдықтар сәйкесінше 
тең болады. Осыдан А1 оқиғасысының ықтималдығы толық ықтималдық формуласымен есетеледі, яғни

ә) Кездейсоқ алынған болттың жарамсыз болсын. Оның ықтималдығы  тең. Онда жарамсыз болттың екінші машина жасағандығының ықтималдығы Бейес формуласымен есептеледі, яғни
тең. Онда жарамсыз болттың екінші машина жасағандығының ықтималдығы Бейес формуласымен есептеледі, яғни

5. Цехта 7 мотор бар. Әрбір мотордың жұмыс істеу ықтималдығы р =0,80-ге тең. Төмендегі берілген оқиғалардың ықтималдықтарын табу керек: а) барлық моторлар жұмыс жасайды; ә) барлық моторлар жұмыс істемейді; б) тек 3 мотор жұмыс істейді; в) 3-тен кем мотор жұмыс істейді; г) 3-тен кем емес мотор жұмыс істейді; ғ) 3-тен артық емес мотор жұмыс істейді; д) 3-тен артық мотор жұмыс істейді; е) ең болмаса бір мотор жұмыс істейді.
Шешуі.  онда
онда
а) 
ә) 
б) 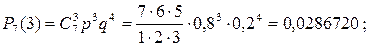
в) 

г) 

немесе 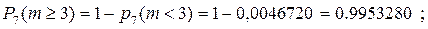
ғ) 

д) 

немесе 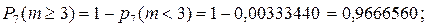
е) 
6. Әр п =100 тәуелсіз тәжірибе нәтижесінде А оқиғасының пайда болу ықтималдығы р =0,8-ке тең. Осы сынау кезінде А оқиғасының а) m =88 рет; ә) m 1 =75-ден кем емес және m 2=90-нан артық емес пайда болу ықтималдығын табу керек.
Шешуі. а) 
Онда 
Қосымша № 1 кестесі бойынша  Осыдан
Осыдан

ә) Лапластың интегралдық теоремасын қолданамыз: Есептің шарты бойынша 
Онда

Лаплас функциясы тақ функция, яғни  болғандықтан
болғандықтан

Қосымша № 2 кестесі бойынша  ,
,
осыдан 
7. Математикалық үміті  және дисперсиясы
және дисперсиясы  ықтималдығы
ықтималдығы  тең болатын Х дискретті кездейсоқ шамасының
тең болатын Х дискретті кездейсоқ шамасының  екі мән қабылдайды, мұндағы
екі мән қабылдайды, мұндағы  Кездейсоқ шаманың үлестірім заңын жазу керек.
Кездейсоқ шаманың үлестірім заңын жазу керек.
Шешуі. Үлестірім заңы  мұндағы
мұндағы 
 осыдан
осыдан 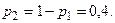 Математикалық үмітпен диспресияның
Математикалық үмітпен диспресияның


формулалары бойынша 
немесе  теңдеулер жүйесін қарастырамыз.
теңдеулер жүйесін қарастырамыз.


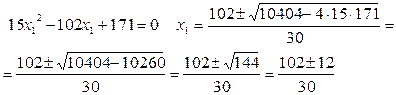
 немесе
немесе 
бірақ  болғандықтан
болғандықтан  болады.
болады.
. Х кездейсоқ шамасының 
интегралдық функциясы берілген. f(x) дифференциалдық функциясын, М(Х) математикалық үмітін, D(X) дисперсиясын тауып, Х кездейсоқ шаманың мәндері (-0,5; 1) интервалына түсу ықтималдығын тап.
Шешуі. Алдымен үлестірім тығыздығын табу керек.

 ,
,



Бақылау сұрақтары
1. Оқиғалардың түрлерін атаңыз.
2. Ықтималдықтың классикалық, геометриялық анықтамалары.
3. Ықтималдықты қосудың негізгі теоремаларын тұжырымдаңыз.
4. Ықтималдықты көбейтудің негізгі теоремаларын тұжырымдаңыз.
5. Толық ықтималдық формуласының мағынасы неде?
6. Бейес формуласының мағынасы неде?
7. Бернулли формуласы.
8. Муавр-Лапластың локальдық және интегралдық теоремалары.
9. Пуассон формуласы.
10. Кездейсоқ шаманың үлестірім заңы.
11. Дискретті кездейсоқ шамалар дегеніміз не?
12. Дискретті кездейсоқ шаманың сандық сипаттамалары.
13. Дискретті кездейсоқ шаманың биномдықүлестірім заңы.
14. Дискретті кездейсоқ шаманың Пуассон үлестірім заңы.
15. Үзіліссіз кездейсоқ шаманың үлестірім функциясы дегеніміз не?
16. Үзіліссіз кездейсоқ шаманың үлестірім тығыздығы дегеніміз не?
17. Үзіліссіз кездейсоқ шаманың сандық сипаттамалары.
18. Үзіліссіз кездейсоқ шаманыңбірқалыпты үлестірім заңы.
19. Үзіліссіз кездейсоқ шаманыңкөрсеткішті үлестірімзаңы.
20. Үзіліссіз кездейсоқ шаманың қалыпты үлестірім заңы.
Не нашли, что искали? Воспользуйтесь поиском: