Образцы решения типовых задач

Задача 1. Решить систему уравнений методом Крамера:

Решение:

Вычислим определитель третьего порядка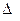

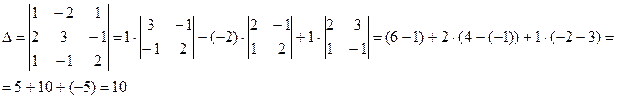
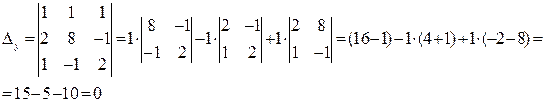
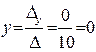
Ответ: , ,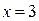

Задача 2. Решить систему уравнений методом обратной матрицы:

Решение:

Обозначим через А – матрицу коэффициентов при неизвестных; Х – матрицу-столбец неизвестных , , 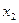, 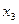Н – матрицу-столбец свободных членов:

; ;

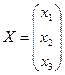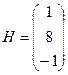
С учетом этих обозначение данная система уравнений примет следующую матричную форму:

Если матрица А – невырожденная (ее определитель отличен от нуля), то она имеет обратную матрицу . Умножив обе части уравнения (4) на получим:

Т.к. (Е – единичная матрица), а 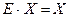, то

Для нахождения решения системы уравнений необходимо вычислить обратную матрицу .

1. Вычислим определитель исходной матрицы: , следовательно матрица имеет себе обратную матрицу

2. Транспонируем матрицу А:

3. Составим матрицу алгебраических дополнений:

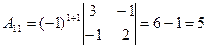
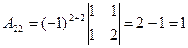
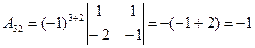
Обратная матрица согласно имеет вид:

Ответ: , ,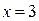

Задача 3. Решить систему уравнений методом Гаусса:

= = =

= = =

Ответ: , ,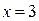

Задача 4. Даны вершины треугольника АВС , ,

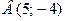Найти:

1. Длину стороны АВ;
2. Уравнение стороны АВ и CD;
3. Внутренний угол А;
4. Уравнение высоты CD и ее длину;
5. Уравнение окружности, для которой высота CD есть диаметр;

Решение:

1. Расстояние 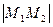между точками и определяется по формуле:

Подставив в эту формулу координаты точек А и В имеем:

2. Уравнение прямой, проходящей через точки и , имеет вид:

Подставив в (2) координаты точек А и В, получим уравнение прямой 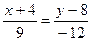АВ

; ;

(АВ)

(АВ):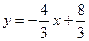

Уравнение прямой (АС):

Подставив в (2) координаты точек А и С:

; ;

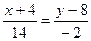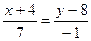
(АС):

3. Угол между двумя прямыми, угловые коэффициенты которых равны и , определяется по формуле:

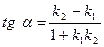
Подставив в данную формулу 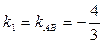, , получим:

4. Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку

Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом k имеет вид: . Подставив координаты точки С и 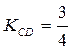, получим уравнение высоты CD:

(CD):

Определим координаты точки D, решив систему уравнений (АВ) и (CD), т.к. точка D получена пересечением этих прямых:

, , ,

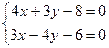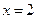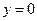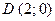
5. Уравнение окружности радиуса К с центром в точке имеет вид:

Т.к. CD - диаметр искомой окружности, то ее центр Е есть середина отрезка CD:

,

,

Используя формулу, получаем уравнение искомой окружности:

Задача 5. Даны векторы , , , . Показать, что векторы , , образуют базис трехмерного пространства и найти координаты вектора в этом базисе.

Решение:

Векторы , , могут образовывать базис трехмерного пространства, если они линейно независимые векторы.

Векторы , , линейно независимы, если в их линейной комбинации, равной нулю, все коэффициенты равны 0.

,

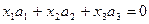Рассмотрим линейную комбинацию векторов

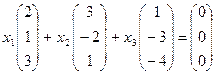
Решим систему уравнений методом Гаусса:

= = =

=

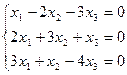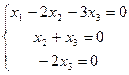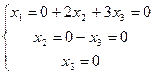
Следовательно, векторы , , линейно независимы и образуют базис трехмерного пространства.

Найдем разложение вектора в этом базисе

= = =

= = = ,

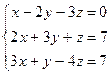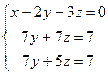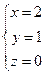Ответ:

Задача 6. Вычислить предел

1.

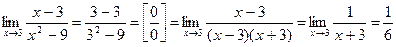
(Метод разложения на множители)

2.

(Метод домножения на сопряженное, I замечательный предел)

3.

(Деление на высшую степень)

4.

(II замечательный предел)

Задача 7. Найти:

Решение:

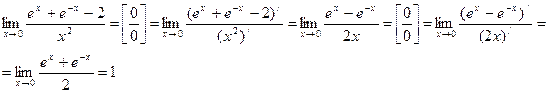
Ответ:

Задача 8. Найти для функции

Решение:

Задача 9. Исследовать функцию:

Общая схема исследования функции:

1. Область определения;

2. Исследование поведения функции в окрестностях точек разрыва, вертикальная асимптота;

3. Горизонтальная, наклонная асимптота;

4. Исследование функции на четность и нечетность

5. Исследование функции на периодичность

6. Точки пересечения с осями координат: с осью , с осью ;

7. Точки экстремума функции;

8. Промежутки знакопостоянства производной (I-е достаточное условие экстремума функции);

9. Промежутки выпуклости (вогнутости), точка перегиба графика функции;

10. График функции

1. Область определения: ,

2. 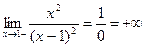, , 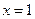- вертикальная асимптота

3. Горизонтальная асимптота:

- горизонтальная асимптота

Наклонная асимптота:

4. 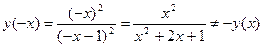, , т.е. функция не является четной и не является нечетной.

5. На периодичность функция не исследуется, т.к. не содержит тригонометрического выражения

6. Точки пересечения с осью

, , ,

- точка пересечения с осями ,

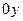
7. Точки экстремума:

- точка экстремума

, , ,

- точка перегиба графика функции

,

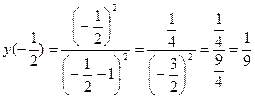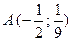
- точка min

Итак: - горизонтальная асимптота

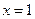- вертикальная асимптота

- точка перегиба графика функции

- точка min

Задача 10.Путём надлежащего преобразования подынтегрального выражения вычислить интеграл: .

Решение:

Не нашли, что искали? Воспользуйтесь поиском: