Переходный электромагнитный процесс при внезапном трёхфазном КЗ в простейшей цепи. Векторные диаграммы, дифференциальные уравнения.

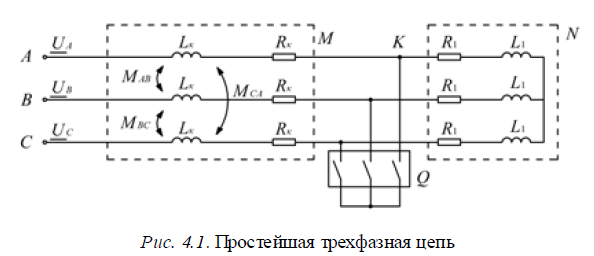
Ответ: Постановка задачи и допущения. Нормальный режим. Трехфазную симметричную цепь с сосредоточенными активными и индуктивными сопротивлениями при отсутствии в ней трансформаторных связей называют простейшей трехфазной цепью. Электромагнитный процесс в такой цепи рассмотрим при допущении, что ее питание осуществляется от источника бесконечной мощности. Такой источник характеризуется неизменностью напряжения на шинах по амплитуде и по частоте. Этому определению соответствуют условия (2.4). Однако любой реальный источник обладает конечной мощностью, но если она во много раз превышает мощность элементов, за которыми рассматривается КЗ, то напряжение на шинах питающей системы изменяется незначительно, что дает возможность в практических расчетах это изменение не учитывать. Кроме того, наличие автоматического регулирования возбуждения (АРВ) дополнительно способствует принятию этого допущения. При принятии этого допущения имеет место преувеличение тока КЗ, что, как правило, не влияет на выбор устанавливаемого оборудования. В качестве основного допущения считаем, что между токами и напряжениями рассматриваемых цепей сохраняется линейная зависимость и, следовательно, они могут быть связаны линейными дифференциальными уравнениями с постоянными коэффициентами. На рис. 4.1 представлена трехфазная симметричная цепь, питаемая источником с неизменным синусоидальным напряжением:

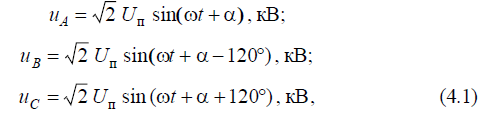где U п – действующее значение напряжения источника питания; – фаза включения – угол между вектором напряжения фазы А и действительной осью (рис. 4.2).

В рассматриваемой схеме емкость фаз относительно земли и друг друга не учитывается вследствие ничтожно малого ее влияния на переходный электромагнитный процесс. Это исключает возможность возникновения колебательных контуров на промышленной частоте, что значительно упрощает анализ протекания переходного процесса в цепи. В нормальном режиме работы цепи по фазам протекает ток, определяемый напряжением источника питания и результирующим сопротивлением:

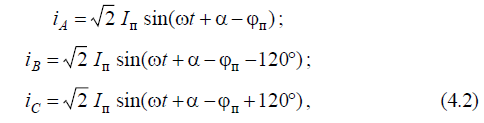где – действующее значение периодической составляющей тока; – полное сопротивление цепи; – активное сопротивление цепи; – индуктивное сопротивление цепи; – угол сдвига между напряжением и током той же цепи. При КЗ в точке K (рис. 4.1) простейшая электрическая цепь распадается на две независимые цепи (обозначим их М и N), одна из которых – М – остается присоединенной к источнику, а другая – N – превращается в короткозамкнутый контур, ток в котором будет поддерживаться до тех пор, пока запасенная в нем энергия магнитногополя не перейдет в тепло, выделяющееся в активном сопротивлении R 1. Для части схемы N дифференциальное уравнение баланса напряжений будет где Решением уравнения (4.3) будет где i 0 – начальное значение свободного тока; T а1 – постоянная времени затухания свободного тока. Уравнение (4.4) показывает, что на участке N имеется лишь свободный ток, который затухает по экспоненциальному закону с постоянной времени T а1, величина которой определяется из выражения

Так как цепь симметрична, то выражение (4.4) правомерно по структуре для всех трех фаз. Начальные значения токов i 0 по фазам будут различны. Векторная диаграмма и осциллограмма протекания переходного

процесса в цепи N представлены на рис. 4.2. Необходимо помнить, что любую синусоидальную величину можно представить в виде неизменного по величине вектора, вращающегося относительно неподвижной оси t–t с частотой вращения w c. Проекции этого вектора на неподвижную ось t–t дают мгновенное значение этого тока. Проекции вращающихся векторов токов IA, IB, IC на ось t–t дают начальные мгновенные значения токов iOA, iOB, iOC, которые затухают с одинаковыми постоянными времени T a1. Касательная к любой точке экспоненты в принятом для оси времени t масштабе дает значение постоянной времени T a1. Это свойство используется для опытного определения постоянных времени затухания апериодических составляющих свободных токов. Для большей точности точку, к которой проводят подкасательную, нужно брать в начальной (более крутой) части кривой. За время t = T а1 апериодический ток уменьшается в e = 2,71 раз или до 1 / e = 0,368 своего начального значения. В соответствии с этим величине T а1 можно дать следующее определение: постоянная времени T a1 – время, в течение которого апериодическая составляющая уменьшается до 0,368 своего начального значения. После затухания апериодической составляющей заканчивается переходный процесс в части цепи N. В одной из фаз свободный ток может отсутствовать, если в момент возникновения КЗ предшествующий ток в этой фазе проходил через нуль. При этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по направлению. Рассмотрим протекание переходного процесса на участке М, получающем питание от источника бесконечной мощности. Так как суммарное сопротивление цепи, к которой присоединен источник, уменьшилось, то ток в общем случае должен увеличиться и должен измениться и угол φ сдвига тока относительно напряжения. Обратимся к векторной диаграмме (рис. 4.3) для начального момента трехфазного КЗ. Пусть векторы характеризуют нормальный режим цепи. Ось абсцисс является осью отсчета углов, а вертикаль t–t является неподвижной осью времени.

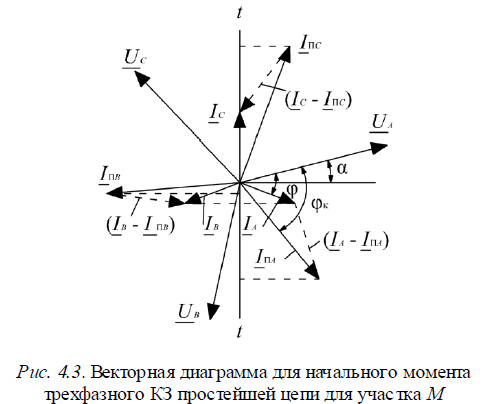В момент КЗ сопротивление цепи М внезапно уменьшается. Следовательно, мгновенно должен возрасти периодический ток этой цепи, причем его сдвиг по фазе также изменится. Напряжение источника сохранится постоянным на все время переходного процесса, а поэтому новое значение периодической составляющей тока не будет затухать. Допустим, что векторы

характеризуют периодический ток установившегоcя режима КЗ. Поскольку цепь содержит индуктивность, то значение полного тока в такой цепи в момент нарушения режима не может измениться скачком. Периодическая же составляющая тока в момент КЗ увеличилась скачкообразно, изменится магнитный поток, обусловленный этой составляющей тока. Изменение магнитного потока вызовет наведение в цепи ЭДС и появление свободной составляющей тока, начальное значение которой полностью компенсирует приращение мгновенного значения периодической составляющей. Это – апериодическая составляющая (на рис. 4.3 для фазы А Таким образом, наряду с периодической составляющей тока КЗ на участке М возникает апериодическая составляющая тока КЗ. Сложение токов периодической и апериодической составляющих дает значение полного тока КЗ. Рассмотрим основные соотношения переходного процесса для участка М. Поскольку при трехфазном КЗ симметрия фаз не нарушается, рассмотрим основные соотношения для одной фазы, например, для фазы А. По второму закону Кирхгофа для любого момента времени имеем соотношение

которое, имея в виду, что iА + iВ + iС = 0, можно представить, опуская

индекс фазы:

где – результирующая индуктивность фазы. Общее решение дифференциального уравнения (4.7) будет

где ZK – полное сопротивление цепи КЗ;  K – аргумент комплексного сопротивления цепи КЗ; 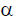– угол, определяющий направление вектора напряжения фазы А при t = 0, или фаза включения. Следовательно, значение тока КЗ определится выражением

где i п – вынужденная (периодическая) составляющая тока КЗ; i a – апериодическая (свободная) составляющая тока КЗ. При рассматриваемых условиях амплитуда периодической составляющей тока КЗ

остается неизменной. Чем больше периодическая составляющая тока, тем больше смещение кривой полного тока относительно оси времени t – t. Мгновенные значения определяются как проекции векторов на ось времени t – t. Поэтому начальное значение i a(o) можно рассматривать как проекцию вектора 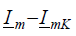на эту линию. При таком представлении наглядно видно, что, в зависимости от момента возникновения КЗ, начальное значение i a(o) может изменяться от возможной наибольшей величины, когда вектор параллелен оси времени, до нуля, когда этот вектор перпендикулярен оси времени. В последнем случае апериодическая составляющая тока в данной фазе отсутствует, так как мгновенное значение предшествующего тока совпадает с мгновенным значением периодической составляющей нового режима.

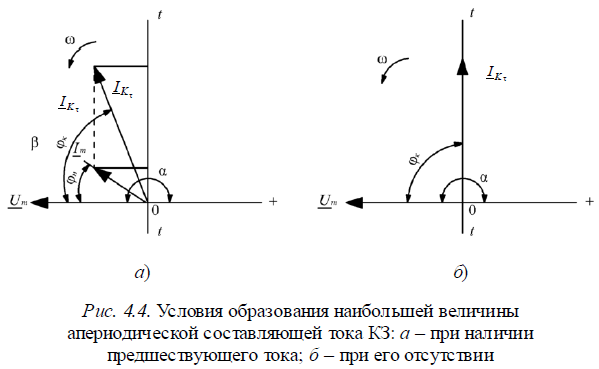
Возможное наибольшее значение апериодической составляющей тока КЗ зависит от фазы включения 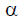и от предшествующего режима цепи. Максимальное значение i a(o) получается при условиях, показанных на рис. 4.4, т. е. когда разность 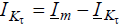параллельна оси времени t – t.

Не нашли, что искали? Воспользуйтесь поиском: