Зависимость сопротивления металлов от температуры.

Сверхпроводимость.

Если металл находится в твердом (или жидком) состоянии, то его атомы пребывают в ионизированном состоянии, т.е. расщепляются на один или несколько электронов и на положительный ион. Эти ионы, располагаясь в узлах кристаллической решетки и совершая лишь небольшие колебания около своих положений равновесия, образуют твердый скелет металлического тела. Отщепленные же ионов так называемые "свободные" электроны беспорядочно движутся в промежутках между ионами, образуя собой особого рода электронный "газ".

В отсутствие внешнего электрического поля электроны эти находятся в совершенно беспорядочном тепловом движении; возникновение же поля ведет к увеличению электронов в направлении действующих на них сил поля, т.е. к появлению электрического тока. Сталкиваясь в своем движении с ионами металла, электроны передают избыток кинетической энергии, приобретенной ими под действием сил поля, что ведет к увеличению энергии теплового движения (колебания) ионов, т.е. к нагреванию металла (выделению джоулева тепла).

С точки зрения этого представления о механизме тока в металлах, ряд наблюдаемых в них явлений получает простое истолкование и объяснение. К числу их относятся, например, термоионные явления, состоящие в испускании металлами в окружающее их пространство потока свободных (в подлинном смысле слова) электронов. При обычных температурах находящиеся в металлах "свободные" электроны не могут выйти за поверхность металла ввиду того, что в поверхностном слое металла они подвергаются действию задерживающих сил, направленных внутрь металла. Но при нагревании металла скорость теплового движения его электронов возрастает, так что при достаточно высоких температурах заметная часть этих электронов приобретает столь большой запас кинетической энергии, что им удается преодолеть тормозящие силы поверхностного слоя и выйти наружу.

Все металлы являются не только хорошими проводниками электричества, но и хорошими проводниками тепла. С точки зрения электронной теории, это совпадение объясняется не простой случайностью, а является следствием одной общей причины – присутствия в металлах свободных электронов. В металлах, в отличие от непроводников, передача тепла осуществляется не только столкновениями атомов, но также, и притом по преимуществу, свободными электронами. Приобретая в нагретом участке добавочную энергию движении, легкоподвижные электроны сравнительно быстро переносят ее в своем движении в смежные участки тела и тем самым значительно ускоряют процесс теплопроводности.

Однако наиболее прямое доказательство того факта, что носителями тока в металлах действительно являются электроны, принесли с собой опыты Толмена, измерившего силу электрических токов, возникающих в металле при сообщении ему ускорения и обусловленных отставанием "свободных" электронов от движения кристаллической решетки металла.

Пусть в единице металла находится n свободных электронов массы m и заряда е. Ввиду беспорядочности движения электронов в отсутствие внешнего электрического поля все направления скорости электронов равновероятны, электронный газ в целом покоится по отношению к положительным ионам решетки и средняя плотность тока равны нулю. Пусть, однако по какой-либо причине возникло добавочное упорядоченное движение электронов относительно решетки со средней скоростью u. При подсчете средней плотности тока j достаточно учесть лишь это упорядоченное движение и можно вовсе пренебречь движением беспорядочным.

Через единицу перпендикулярного вектору u сечения проводника за единицу времени пройдут все электроны, находившиеся от него на расстоянии, меньшем или равном u, т.е. все электроны, расположенные в цилиндре сечения 1 и высоты u (см. рис. 4). Число их равно nu, несомый же ими заряд равен enu; стало быть,

. (5.1)

Воспользуемся этой формулой, чтобы определить зависимость электропроводности металла от других физических величин, характеризующих его свойства. В первом приближении будем рассматривать "электронный газ" в металле как газ идеальный, т.е. будем считать, что в промежутках между столкновениями с другими электронами и ионами электроны движутся по законам движения материальных точек, подверженных действию лишь силы внешнего (макроскопического) поля E.

В отсутствие внешнего поля Е средняя скорость электронов относительно решетки равна нулю. Под воздействием поля Е электроны приобретают некоторую добавочную скорость u, параллельную действующей на них силе е Е. Это накопление скорости, параллельной силе е Е, происходит лишь во время свободного полета электронов между двумя последовательными столкновениями его с ионами решетки. При каждом таком столкновении направление и величина скорости электрона изменяется по закону случая. Стало быть непосредственно после столкновения среднее значение u равно нулю, а непосредственно перед столкновением

,

где равно ускорению, сообщаемому силой е Е, а τ – обозначает среднюю продолжительность свободного полета электронов. Таким образом, среднее значение u равно

.

С другой стороны, если l есть длина свободного пробега электрона, то

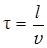
где v – средняя скорость беспорядочного движения электронов в отсутствие внешнего поля, ибо во всех практически интересных случаях v >> u, и поэтому при подсчете среднего численного (а не векторного) значения скорости электрона добавочной скоростью u можно пренебречь

Внося полученные нами выражения в (5.1), получим:

.

Таким образом, плотность тока оказывается пропорциональной напряженности поля Е, как того требует закон Ома (2.6), коэффициент пропорциональности, т.е. электропроводность металла λ, оказывается равной

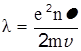. (5.2)

Предположим, что к электронам в металле приложима классическая статистическая механика. Согласно основным положениям этой механики, средняя энергия поступательного теплового движения молекул любого газа зависит лишь от абсолютной температуры Т, но не от химической природы и молекулярного веса газа и равна:

, (5.3)

где k – постоянная Больцмана. Применяя это соотношение к электронному газу в металле, получим из (5.2):

. (5.4)

Существует одно явление, механизм которого смогла полностью объяснить лишь квантовая теория. Это явление сверхпроводимости.

Сопротивление всех чистых (лишенных примесей) металлов при приближении к абсолютному нулю температуры стремится к нулю (примерно, как Т⁵), но в некоторых металлах изменение это происходит не плавно: при некоторой вполне определенной температуре сопротивление внезапно (скачком) падает до нуля или, во всяком случае, до неизмеримо малой величины. Резкость этого скачка характеризуется тем, что в некоторых металлах он происходит при изменении Т всего на 0,001⁰.

Температура скачка называется критической температурой Т_с, а состояние металла ниже этой температуры, характеризуемое отсутствием сопротивления постоянному току, называется сверхпроводящим состоянием. Явления сверхпроводимости экспериментально установлены примерно у 20 чистых металлов и у ряда сплавов.

Поскольку в сверхпроводящем состоянии металлов сопротивление равно нулю, в них не должно иметь место выделение джоулева тепла, и токи, раз возникнув, должны сохраняться неопределенно долгое время в отсутствие всякой сторонней э.д.с. Следует однако отметить, что в полях высокой частоты в сверхпроводниках происходит выделение джоулева тепла.

Сверхпроводящее состояние отличается от других состояний вещества еще одной особенностью: магнитное поле в глубь сверхпроводников не проникает, т.е. напряженность и индукция магнитного поля внутри сверхпроводников равны нулю. Этот факт, в связи с выявившейся обратимостью перехода металлов при критической температуре в сверхпроводящее состояние, лег в основу термодинамической теории проводимости, в которой переход металлов в сверхпроводящее состояние рассматривается как фазовый переход и которая позволила количественно связать между собой магнитные и тепловые характеристики сверхпроводников.

Не нашли, что искали? Воспользуйтесь поиском: