
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
АРИФМЕТИЧЕСКИЕ И ГЕОМЕТРИЧЕСКИЕ ПРОГРЕССИИ
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана числовая последовательность х 1, х 2, …, хn, ….
Обозначение числовой последовательности { хn }.
При этом числа х 1, х 2, …, хn, … называются членами последовательности.
Основные способы задания числовых последовательностей
1. Одним из наиболее удобных способов является задание последовательности формулой её общего члена: хn = f (n), n Î N.
Например, хn = n 2 + 2 n + 3 Þ х 1 = 6, х 2 = 11, х 3 = 18, х 4 = 27, …
2. Непосредственным перечислением конечного числа первых членов.
Например, 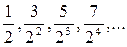 Þ
Þ 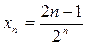
3. Рекуррентным соотношением, т.е. формулой, выражающей n-член через предшествующие один или несколько членов.
Например, рядом Фибоначчи называется последовательность чисел
1, 1, 2, 3, 5, 8, 13, 21, …, которая определяется рекуррентно:
х 1 = 1, х 2 = 1, хn +1 = xn + xn –1 (n = 2, 3, 4, …).
Арифметические операции над последовательностями
1. Суммой (разностью) последовательностей { аn } и { bn } называется последовательность { cn } = { an ± bn }.
2. Произведением последовательностей { аn } и { bn } называется последовательность { cn } = { an × bn }.
3. Частным последовательностей { аn } и { bn }, bn ¹ 0, называется последовательность { cn } = { an ×/ bn }.
Свойства числовых последовательностями
1. Последовательность { хn } называется ограниченной сверху, если существует такое действительное число М, что для всех натуральных значений n справедливо неравенство хn £ M.
2. Последовательность { хn } называется ограниченной снизу, если существует такое действительное число m, что для всех натуральных значений n справедливо неравенство хn ³ m.
3. Последовательность { хn } называется возрастающей, если для всех натуральных значений n справедливо неравенство хn < хn +1.
4. Последовательность { хn } называется убывающей, если для всех натуральных значений n справедливо неравенство хn > хn +1.
5. Последовательность { хn } называется невозрастающей, если для всех натуральных значений n справедливо неравенство хn ³ хn +1.
6. Последовательность { хn } называется неубывающей, если для всех натуральных значений n справедливо неравенство хn £ хn +1.
Последовательности возрастающие, убывающие, невозрастающие, неубывающие называются монотонными последовательностями, при этом возрастающие и убывающие – строго монотонными.
Основные приёмы, применяемые при исследовании последовательности на монотонность
1. Использование определения.
а) Для исследуемой последовательности { хn } составляется разность
хn – хn +1, и далее выясняется, сохраняет ли эта разность постоянный знак при любых n Î N, и если да, то какой именно. В зависимости от этого делается вывод о монотонности (немонотонности) последовательности.
б) Для знакопостоянных последовательностей { хn } можно составить отношение хn +1/ хn и сравнить его с единицей.
Если это отношение при всех n больше единицы, то для строго положительной последовательности делается вывод о её возрастании, а для строго отрицательной, соответственно, об убывании.
Если это отношение при всех n не меньше единицы, то для строго положительной последовательности делается вывод о её неубывании, а для строго отрицательной, соответственно, о невозрастании.
Если это отношение при некоторых номерах n больше единицы, а при других номерах n меньше единицы, то это говорит о немонотонном характере последовательности.
2. Переход к функции действительного аргумента.
Пусть необходимо исследовать на монотонность числовую последовательность
аn = f (n), n Î N.
Введём в рассмотрение функцию действительного аргумента х:
f (х) = а (х), х ³ 1,
и исследуем её на монотонность.
Если функция дифференцируема на рассматриваемом промежутке, то найдём её производную и исследуем знак.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
Возвращаясь к натуральным значениям аргумента, распространяем эти результаты на исходную последовательность.
Число а называется пределом последовательности хn, если для любого сколь угодно малого положительного числа e найдётся такое натуральное число N, что для всех номеров n > N выполнено неравенство | xn – a | < e.
а = 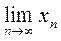
Вычисление суммы n первых членов последовательности
1. Представление общего члена последовательности в виде разности двух или нескольких выражений таким образом, чтобы при подстановке большая часть промежуточных слагаемых сократилась, и сумма существенно упростилась.
2. Для проверки и доказательства уже имеющихся формул нахождения сумм первых членов последовательностей может быть использован метод математической индукции.
3. Некоторые задачи с последовательностями удаётся свести к задачам на арифметические или геометрические прогрессии.
Арифметические и геометрические прогрессии
| Арифметическая прогрессия | Геометрическая прогрессия |
| Определение Числовая последовательность { хn }, n Î N, называется арифметической прогрессией, если каждый её член, начиная со второго, равен предыдущему, сложенному с одним и тем же постоянным для данной последовательности числом d, т.е. аn +1 = an + d, где d – разность прогрессии, аn – общий член (n -й член) | Определение Числовая последовательность { хn }, n Î N, называется геометрической прогрессией, если каждый её член, начиная со второго, равен предыдущему, умноженному на одно и то же постоянное для данной последовательности числом q, т.е. bn +1 = bn × q, b 1 ¹ 0, q ¹ 0, где q – знаменатель прогрессии, bn – общий член (n -й член) |
| Монотонность Если d > 0, то прогрессия возрастающая. Если d < 0, то прогрессия убывающая. | Монотонность Если b 1 > 0, q > 1 или b 1 < 0, 0 < q < 1, то прогрессия возрастающая. Если b 1 < 0, q > 1 или b 1 > 0, 0 < q < 1, то прогрессия убывающая. Если q < 0, то прогрессия немонотонная |
| Формула общего члена аn = a 1 + d ×(n – 1) Если 1 £ k £ n – 1, то аn = ak + d ×(n – k) | Формула общего члена bn = b 1 × qn – 1 Если 1 £ k £ n – 1, то bn = bk × qn – k |
Характеристическое свойство
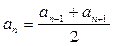 Если 1 £ k £ n – 1, то
Если 1 £ k £ n – 1, то 
| Характеристическое свойство
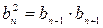 Если 1 £ k £ n – 1, то
Если 1 £ k £ n – 1, то 
|
| Свойство an + am = ak + al, если n + m = k + l | Свойство bn × bm = bk × bl, если n + m = k + l |
Сумма первых n членов
Sn = a 1 + a 2 + … + an
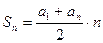 или или 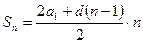
| Сумма
Sn = b 1 + b 2 + … + bn
Если q ¹ 1, то 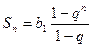 .
Если q = 1, то Sn = b 1× n.
Если | q | < 1 и n ® ¥, то .
Если q = 1, то Sn = b 1× n.
Если | q | < 1 и n ® ¥, то 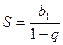
|
| Операции над прогрессиями 1. Если { аn } и { bn } арифметические прогрессии, то последовательность { an ± bn } тоже является арифметической прогрессией. 2. Если все члены арифметической прогрессии { аn } умножить на одно и то же действительное число k, то полученная последовательность тоже будет арифметической прогрессией, разность которой соответственно изменится в k раз | Операции над прогрессиями Если { аn } и { bn } геометрические прогрессии со знаменателями q 1 и q 2 соответственно, то последовательность: 1) { an × bn } тоже является геометрической прогрессией со знаменателем q 1× q 2; 2) { an / bn } тоже является геометрической прогрессией со знаменателем q 1/ q 2; 3) {| an |} тоже является геометрической прогрессией со знаменателем | q 1| |
Основные методы решения задач на прогрессии
1. Один из наиболее распространённых методов решения задач на арифметические прогрессии состоит в том, что все задействованные в условии задачи члены прогрессии выражаются через разность прогрессии d и какой-либо один его член, чаще всего первый a 1. Исходя из условий задачи, составляется и решается система с неизвестными d и а 1.
2. Широко распространён и считается стандартным метод решения задач на геометрические прогрессии, когда все фигурирующие в условии задачи члены геометрической прогрессии выражаются через знаменатель прогрессии q и какой-либо один его член, чаще всего первый b 1. Исходя из условий задачи, составляется и решается система с неизвестными q и b 1.
Образцы решения задач
Задача 1.
Задана последовательность хn = 4 n (n 2 + 1) – (6 n 2 + 1). Найти сумму Sn первых n членов этой последовательности.
Решение. Преобразуем выражение для общего члена последовательности:
хn = 4 n (n 2 + 1) – (6 n 2 + 1) = 4 n 3 + 4 n – 6 n 2 – 1 = n 4 – n 4 + 4 n 3 – 6 n 2 + 4 n – 1 =
= n 4 – (n 4 – 4 n 3 + 6 n 2 – 4 n + 1) = n 4 – (n – 1)4.
Sn = x 1 + x 2 + x 3 + … + xn = (14 – 04) + (24 – 14) + (34 – 24) + … + (n 4 – (n – 1)4) = n 4.
Задача 2.
Задана последовательность аn = 3 n + 2. Вычислить сумму 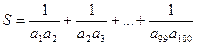 .
.
Решение. Каждое слагаемое суммы S имеет вид
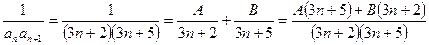 .
.
Отсюда, A (3 n + 5) + B (3 n + 2) = 1,
(3 A + 3 B) n + (5 A + 2 B) = 1.
Приравняем коэффициенты при соответствующих степенях n.
n 1 | 3 A + 3 B = 0,
n0 | 5 A + 2 B = 1.
Решая полученную систему, получим А = 1/3, В = –1/3.
Таким образом, 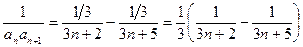 , и
, и
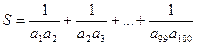 =
= 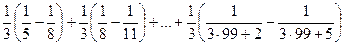 =
=
= 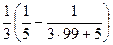 =
= 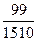 .
.
Задача 3.
Последовательность задана рекуррентно а 1 = 2, аn +1 = 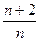 аn. Является ли число 1980 членом этой последовательности? Если да, то определить его номер.
аn. Является ли число 1980 членом этой последовательности? Если да, то определить его номер.
Решение. Выпишем первые n членов этой последовательности:
а 1 = 2, 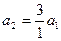 ,
,  ,
,  ,
, 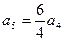 ,…,
,…, 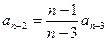 ,
, 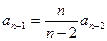 ,
,  .
.
Перемножим эти равенства:
а 1 а 2 а 3 а 4 а 5… an -2 an -1 an = 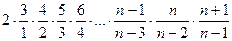 а 1 а 2 а 3 а 4 а 5… an -2 an -1.
а 1 а 2 а 3 а 4 а 5… an -2 an -1.
Отсюда, an = n (n + 1).
Тогда, 1980 = n (n + 1) Û n 2 + n – 1980 = 0 Û n = –45 < 0, n = 44 Î N.
Ответ: да, n = 44.
Задача 4.
Найти сумму S = а 1 + а 2 + а 3 + … + аn чисел а 1, а 2, а 3, …, аn, которые при любом натуральном n удовлетворяют равенству Sn = а 1 + 2 а 2 + 3 а 3 + … + nаn = 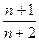 .
.
Решение. S 1 = a 1 = 2/3.
Для n > 1, nan = Sn – Sn –1 = 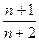 –
–  =
= 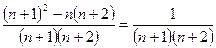 .
.
Отсюда, 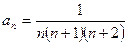 =
= 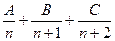 =
=  ,
,
А (n + 1)(n + 2) + Bn (n + 2) + Cn (n + 1) = 1
(A + B + C) n 2 + (3 A + 2 B + C) n + 2 A = 1,
Приравняем коэффициенты при соответствующих степенях n.
n 2 | A + B + C = 0,
n 1 | 3 A + 2 B + C = 0,
n0 | 2 A = 1.
Решая полученную систему, получим А = 1/2, В = –1, C = 1/2.
Итак, 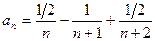 =
=  =
=  =
= 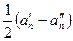 ,
,
где 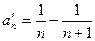 ,
, 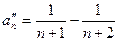 , n > 1,
, n > 1,
S ¢ = 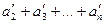 =
= 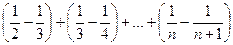 =
= 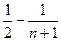 .
.
S ¢¢ = 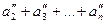 =
= 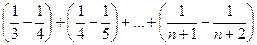 =
= 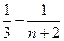 .
.
S = а 1 + а 2 + а 3 + … + аn = а 1 +  =
=
= а 1 + 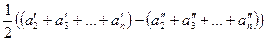 = а 1 +
= а 1 + 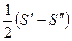 =
=  =
=
=  .
.
Задача 5.
Найти наибольший член последовательности  .
.
Решение. Положим bn = – n 2 + 8 n –7 = 9 – (n – 4)2,  .
.
Последовательность { bn } достигает своего максимума при n = 4, а последовательность { сn } – при n = 3. Кроме того, при 1 £ n £ 3 обе последовательности возрастают (b 1 < b 2 < b 3, c 1 < c 2 < c 3), а при n ³ 4 – убывают
(b 4 > b 5 > …, c 4 > c 5 > …). Поэтому своё наибольшее значение их сумма может достигать при n = 3 или при n = 4. Так как а 3 = 11 > а 4 = 10,5, то приходим к ответу:
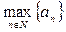 = а 3.
= а 3.
Задача 6.
Вычислить сумму первых 100 членов последовательности { n /5 n }.
Решение. Воспользуемся следующим полезным приёмом.
 .
. 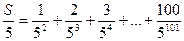 .
.
S – 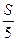 =
=  =
=  =
=  .
.
Отсюда, S = 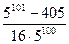 .
.
________________________________________________________________
Задания для самостоятельного решения
1. Даны числа х 1, х 2, …, х 1983, такие, что х 1 = х 2013 = 2013 и 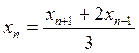 при n = 2, 3, …, 2012. Докажите, что все числа xn равны 2013.
при n = 2, 3, …, 2012. Докажите, что все числа xn равны 2013.
2. Последовательность (хn) задана рекуррентно следующим образом: х 1 = 0 и хn +1 = 5 xn + 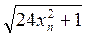 для n = 1, 2, …. Докажите, что все члены последовательности, начиная со второго, являются натуральными числами.
для n = 1, 2, …. Докажите, что все члены последовательности, начиная со второго, являются натуральными числами.
3. Члены последовательности (an) определяются рекуррентным способом: 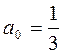 и
и  при n = 1, 2, …. Докажите, что последовательность (an) монотонна.
при n = 1, 2, …. Докажите, что последовательность (an) монотонна.
4. Длины сторон треугольника образуют арифметическую прогрессию, разность d которой положительна. Докажите, что в этом треугольнике есть два угла, меньшие 60о.
5. Найдите три различных натуральных числа, образующих арифметическую прогрессию и таких, что их произведение является полным квадратом.
6.Вычислите сумму 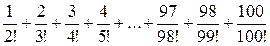 .
.
7. Последовательность (an) задана формулой  , где n Î N. Найти сумму первых 2013 членов последовательности.
, где n Î N. Найти сумму первых 2013 членов последовательности.
8. Последовательность (an) задана формулой  . Вычислить сумму S = a 1 + a 2 + a 3 + a 4 + a 5 + …
. Вычислить сумму S = a 1 + a 2 + a 3 + a 4 + a 5 + …
9. Последовательность (an) задана формулой  , где n Î N. Найти сумму первых 100 членов последовательности.
, где n Î N. Найти сумму первых 100 членов последовательности.
10. Целые числа a, b, c образуют геометрическую прогрессию. Может ли последняя цифра в десятичной записи числа N = a 3 + b 3 + c 3 – 3 abc быть равной 0, а предпоследняя цифра при этом быть равной 2?
11. Найдите наименьший член последовательности (аn), где 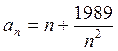 .
.
12. Докажите, что не существует строго возрастающей последовательности целых неотрицательных чисел а 1, а 2, а 3, …, для которой при любых n и m выполняется соотношение аmn = am + an.
13. Найдите 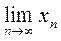 , если числа xn определяются рекуррентными соотношениями
, если числа xn определяются рекуррентными соотношениями 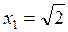 и
и  для n Î N.
для n Î N.
14. Последовательности (an) и (bn) заданы рекуррентным способом: а 1= а >0, b 1= b >0, 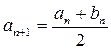 ,
, 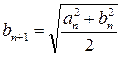 для n ³ 1. Докажите, что при любом n выполняется неравенство
для n ³ 1. Докажите, что при любом n выполняется неравенство 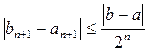 .
.
15. Вычислите предел последовательности { an }, где { an } – дробная часть числа 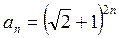 .
.
16. Числа an, bn определяются рекуррентными соотношениями a 1 = b 1 = 1 и an +1 = an + 3 bn, bn +1 = an + bn для натуральных n ³1. Докажите, что последовательность  имеет предел. Найдите этот предел.
имеет предел. Найдите этот предел.
| <== предыдущая лекция | | | следующая лекция ==> |
| Расход на оплату труда (Роn) | | | Песни к празднику Последний звонок: учителю физкультуры |
Не нашли, что искали? Воспользуйтесь поиском: