Практическое занятие 11

Численное интегрирование.

Цель занятия

Знакомство студентов с методом численного интегрирования Гаусса и вычисление вероятности возникновения искрового перекрытия с опоры на провод ВН при ударе молнии в опору.

Общие сведения о перенапряжениях при ударе молнии в опору

При ударе молнии в опору линии электропередачи по опоре протекает ток молнии и создаёт на сопротивлении заземления опоры (у основания опоры) напряжение в соответствии с законом Ома U = I_m*R _и. Опора ЛЭП имеет индуктивность, которая зависит от типа опоры и её высоты. В табл. 11.1. приведены удельные индуктивности (L _уд) различных типов опор.

Таблица 11.1. Удельные индуктивности (L _уд) различных типов опор

Ток молнии достигает своего максимального значения за некоторое время (4 ÷ 8 мкс или 1 мкс), называемое длительностью фронта молнии Т1. Для упрощения расчётов принимается, что нарастание тока происходит линейно с крутизной a = I_m / T 1. На индуктивности опоры возникает напряжение , где h _тр - высота верхней траверсы опоры. Суммарное напряжение на опоре (на верхней траверсе опоры) определяется:

, (11.1)

где 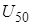- напряжение, при котором происходит искровое перекрытие с опоры на провод ВН (с вероятностью 50% для импульсных напряжений).

Ток молнии и крутизна тока молнии величины случайные с некоторым распределением вероятностей появления. Так вероятность обнаружить молнию с током больше I_m можно определить по одной из формул:

или (11.2)

а вероятность обнаружить молнию с крутизной больше чем а - по формуле:

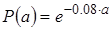(11.3)

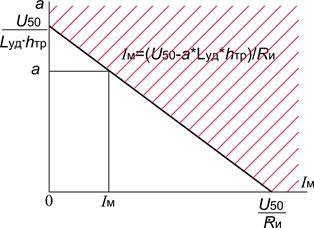
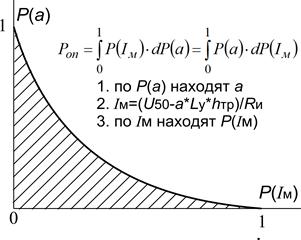
Для определения вероятности искрового пробоя между опорой и проводом ВН нужно найти вероятности всех возможные значения тока молнии и крутизны тока молнии, при которых выполняется (11.1). Если по осям отложить значения крутизны и тока молнии, то все значения, при которых выполняется (11.1) находятся в опасной зоне, заштрихованной красными линиями (рис. 11.1а). Более удобное для расчёта представление зоны опасных параметров получается в осях вероятностей рис. 11.1б). 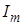Вероятность обнаружить молнию с каким-либо током и с какой-либо крутизной лежит в диапазоне от 0 до 1. Для определения вероятности искры Р _оп достаточно найти площадь под кривой опасных параметров рис. 11.1б, т.е. вычислить определённый интеграл, представленный на рис. 11.1б.

а)

б)

Рис. 11.1 Зона опасных параметров (а) и вероятность искрового перекрытия (площадь заштрихованной области) (б)

Для вычисления определённых интегралов разработано множество различных методов. Одним из таких методов численного интегрирования является метод Гаусса. Метод заключается в разбиении площади на множество мелких элементарных площадей таким образом, чтобы одну из сторон можно было заменить прямой линией. Применим этот метод для вычисления вероятности искрового перекрытия с опоры на провод. Разделим весь интервал возможных значений вероятности крутизны молнии на 1000 частей и определим площадь одной произвольной части. Эта часть ограничена в двух сторон параллельными оси х прямыми линиями, отстоящими друг от друга на расстоянии D у. С третьей стороны площадки расположена ось у, а с четвёртой стороны -кривая опасных параметров. При малых расстояниях D у между линиями кривую опасных параметров можно заменить прямой. Тогда эта элементарная площадь превращается в прямоугольную трапецию, площадь которой равна полусумме оснований умноженной на высоту. Эту же площадь трапеции можно представить в виде площади прямоугольника у которого одна сторона равна D у, а другая вероятности тока молнии с опасными параметрами. Площадь под кривой опасных параметров будет равна сумме всех элементарных площадей. В примере величина D у = 0,001. Тогда алгоритм расчёта вероятности искрового перекрытия будет состоять в повторении 1000 раз следующих действий:

1. задаётся вероятность середины интервала D у = 0,001 ( = 0,0005);

2. находится крутизна молнии, соответствующая этой вероятности в соответствии с формулой (11.3) a = Ln()/(-0.08);

3. по формуле (11.1) находится ток молнии, при котором возникает перекрытие: . При расчёте по этой формуле может оказаться так, что числитель станет отрицательным. Это означает, что для перекрытия достаточно второго слагаемого в (11.1) и ток равен 0. Это ограничение выглядит как условие: если 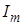< 0, тогда току молнии присвоить значение 0 (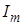:= 0);

4. по найденному току молнии определить вероятность возникновения молнии с таким током в соответствии с (11.2).

5. вычислить площадь элементарной трапеции ;

6. добавить вычисленную площадь dS к переменной, в которой эта площадь будет накапливаться.

Задание 1

ЗапуститеДельфи. Создайте заголовок формы «Расчёт вероятности искры при ударе молнии в опору». Сохраните программу в папке практика 11. Проверьте число сохранённых файлов (должно быть не менее 6).

Положите на форму компонент Panel, удалите её заголовок и измените цвет на clSkyBlue.

Положите на панель следующие компоненты: а) одну из трёх типов кнопок запуска Button и измените её заголовок на «Старт»; б) 5 компонент LabeledEdit из дополнительной палитры компонентов и измените их заголовки на следующие: «высота опоры, м», «длина гирлянды, м» и «Unom, кВ», «удельная индуктивность, мкГн», «R импульсное, Ом». В поля Text компонентов впишите 22, 1,2, 110, 0,7 и 5 соответственно. Измените размеры панели так, чтобы компоненты занимали большую часть площади панели, а саму панель с компонентами переместите в верхний левый угол формы. Положите на форму под панелью отладочное поле вывода Memo, выровняйте его по ширине с панелью, измените вертикальный размер до края формы и вставьте линейки прокрутки.

Положите на форму справа от панели компонент Chart из дополнительного набора и измените его размер так, чтобы он занимал всю оставшуюся часть формы. Подготовьте компонент Chart к выводу графиков.

Задание 2

Двойным щелчком на кнопке «Старт» создайте заготовку процедуры. В разделе описания переменных опишите переменные с плавающей запятой Hop, L, Lgir, Lud, Unom, U50, Ri, sum, Im, Pim, a, Pa и две целочисленные переменные n, i.

В теле цикла обнулите значение переменной sum (sum:=0;) и очистите графики (Chart1.series[0].clear;).

Введите значения пяти переменных из компонент LabeledEdit (Hop - высота опоры до верхней траверсы; Lgir - длина гирлянды; Unom - номинальное напряжение ЛЭП; Lud - удельная индуктивность; Ri - импульсное сопротивление заземления опоры). Выведите значения переменных в поле memo.

Вычислите импульсную прочность гирлянды изоляторов, которая равна напряжению импульсов, при котором возникает искра вдоль гирлянды в 50 случаев из 100 поданных импульсов, Обычно обозначается символом U 50% и называется пятидесятипроцентным напряжением:

U 50:=500* Lgir; {в кВ}.

Вычислите индуктивность опоры от земли до верхней траверсы с учётом взаимной индуктивности с каналом молнии:

L:=1.24* Hop* Lud;{в мкГн. 1.24- коэффициент взаимоиндукции}.

Создайте заготовку цикла интегрирования по всем возможным значениям вероятности амплитуды тока молнии и крутизны фронта молнии:

for i:=1 to 1000 do

begin

end; {for i}

В тело цикла вставьте последовательность интегрирования, которая приведена в разделе описания алгоритма расчёта с выравниванием по позиции на 1-2 пробела правее первой позиции начала цикла begin:

pa:=(i -0.5)*0.001; // вероятность обнаружения молнии с некой крутизной

//- пробегает все значения от 0 до 1 с шагом 0,001;

a:=-ln(pa)/0.064; //определение крутизны фронта молнии по заданной вероятности;

im:=(u50-a*L)/ Ri; //Ток молнии, при котором происходит перекрытие гирлянды;

if im <0 then im:=0; //ограничение, поскольку ток молнии не может быть < 0 по модулю;

pim:=1/(1+0.0021* im +0.00014*sqr(im)+0.000024* im *sqr(im));

//pim - вероятность обнаружить ток молнии, достаточный для искры;

sum:= sum+pim /1000; //суммирование.

После выхода из цикла в переменной накопится значение вероятности искры (результат интегрирования). Выведите это значение в поле memo так, чтобы было понятно, что выводится. Измените несколько раз значения Ri, Lud, Hop, Lgir, Unom и ответьте на вопрос: как изменяется вероятность возникновения искрового пробоя воздуха вдоль гирлянды изоляторов (обратное перекрытие) от этих параметров.

Задание 3

Постройте график зависимости вероятности пробоя от изменения сопротивления заземления опоры. Для этого перед циклом по I вставьте начало цикла по n:

for n:=1 to 1000 do

begin

и определите возможный диапазон изменения переменной. Например для импульсного заземления можно задать диапазон 2 -102 Ома и шагом 0.1:

Ri:=2+n/10;.

Далее должен следовать цикл по i, созданный ранее. После команды вывода в поле memo вставьте команду построения графика:

Chart1.series [0]. AddXY (Ri, sum *1000);

И закройте цикл по n:

end; {for n}.

Запустите программу на исполнение, исправьте ошибки.

Не нашли, что искали? Воспользуйтесь поиском: