Транспортная задача. Основным здесь является, как правило, распределение ресурсов, находящихся у n производителей (поставщиков)

Основным здесь является, как правило, распределение ресурсов, находящихся у n производителей (поставщиков), по m потребителям этих ресурсов (клиентам).

Наиболее часто встречаются следующие задачи, которые приводятся к транспортным:

- прикрепление потребителей ресурса к производителям;

- привязка пунктов отправления к пунктам назначения;

- взаимная привязка грузопотоков прямого и обратного направлений;

- оптимальная загрузка промышленного оборудования;

- оптимальное распределение объемов выпуска продукции между предприятиями и др.

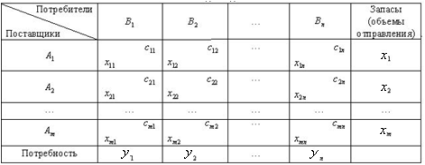
В общем виде исходные данные представлены в таблице 1. Строки транспортной таблицы соответствуют пунктам отправления (в последней клетке каждой строки указан объем запаса продукта x_i ), а столбцы — пунктам назначения (послед­няя клетка каждого столбца содержит значение потребности y_j). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о пе­ревозке из i -го пункта в j -й: в правом верхнем углу находится цена перевозки единицы продукта, а в левом нижнем — значе­ние объема перевозимого груза для данных пунктов.

Таблица 1

Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения:

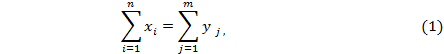
Если такого равенства нет (потребности выше запасов или наоборот), то задачу называют открытой, т.е.:

Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):

В транспортных задачах должны соблюдаться следующие условия:

- рассматриваются однородные ресурсы;

- условия задачи описываются только уравнениями;

- все переменные выражаются в одинаковых единицах измерения;

Решение начинается с составления некоторого опорного плана задачи (допустимого плана перевозок).

Существует два основных метода нахождения опорных планов:

1) метод северо-западного угла (или диагональный метод);

2) метод наименьшей стоимости (минимального тарифа).

Эти методы отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода.

а) Метод северо-западного угла

При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) остав­шейся части таблицы. Заполнение таблицы начи­нается с клетки неизвестного x ₁₁ и заканчивается в клетке неизвест­ного x_mn, т. е. идет как бы по диагонали таблицы перевозок (см. таблицу 2):

Пример:

Таблица 2

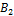
				Объемы
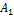
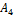
Потребности

Заполнение таблицы начинается с ее северо-западного угла, т.е. клетки с неизвестным x ₁₁. Первая база A ₁ может частично удовле­творить потребность первого заказчика B ₁ (x ₁=80, y ₁=120, x ₁ < y ₁).

Вписываем значение x ₁₁= 80 в клетку x ₁₁ и исключаем из рассмотрения первую строку. Заказчику B ₁ требуется еще объем 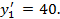В оставшейся новой таблице с тремя строками A ₂ ,A ₃ A ₄ и тремя столбцами B ₁ ,B ₂ ,B ₃, северо-западным углом будет клетка для неизвестного x ₂₁. Вторая база с запасом может полностью удовлетворить потребность первого заказчика B ₁ (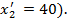

Вписываем значение x ₂₁ = 40 в клетку x ₂₁ и исключаем из рассмотрения первый столбец. На базе A ₂ остается остаток (запас) 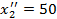. В оставшейся новой таблице с тремя строками A ₂ ,A ₃ A ₄ и двумя столбцами B ₂ ,B ₃ северо-западным углом будет клетка для неизвестного x ₂₂. Теперь заказчик B ₂ может принять с базы A ₂ объем 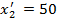и у него останется еще не удовлетворенная потребность .

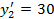Вписываем значение x ₃₂ = 30 в клетку x ₃₂ и исключаем из рассмотрения второй столбец. Потребность второго заказчика B ₂ полностью удовлетворена (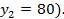

Теперь переходим к заполнению клетки для неизвестного x ₃₃ и т.д.

В результате у нас останется одна база A ₄ с запасом груза и один пункт B ₃ с потреб­ностью y ₃=70. Соответственно этому имеется одна свободная клетка, которую и заполняем, положив x ₄₃=70. План составлен. Базис образован неизвестными x ₁₁ ,x ₂₁ ,x ₂₂ ,x ₃₂ ,x ₃₃ ,x ₄₃.

Число заполняемых клеток в базисе должно быть равно m+n- 1.

Правиль­ность составленного плана можно проверить, подсчитав суммы чисел, стоящих в заполненных клетках по строкам и столбцам.

Общий объем перевозок для этого плана составит:

б) Метод минимального тарифа

При этом методе на каждом шаге построения опорного плана первой заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них (см. таблицу 3):

Таблица 3

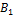
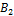
				Объемы
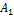
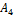
Потребности

В данном случае заполнение таблицы начинается с клетки для неизвест­ного x ₃₂, для которого мы имеем значение c ₃₂ = 1, наименьше из всех значений c_ij. Эта клетка находится на пересечении третьей строки и второго столбца, соответствующим третьей базе A ₃ и вто­рому заказчику B ₂. Третья база A ₃ не может полностью удовлетворить потребность второго заказчика B ₂ (x ₃=60, y ₂=80, x ₃ < y ₂).

Вписываем значение x ₃₂ = 60 в клетку x ₃₂. У заказчика B ₂ останется не удовлетворенная потребность .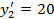

Этот объем мы можем взять с базы A ₄ 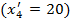и полностью удовлетворить потребность второго заказчика B ₂ (y ₂=80). Исключаем из рассмотрения второй столбец. В оставшейся новой таблице с четырьмя строками A ₁ ,A ₂ ,A ₃ A ₄ и двумя столбцами B ₁ ,B ₃ клеткой с наименьшим значе­нием c_ij будет клетка c ₁₁=2.

Заполняем описанным выше способом эту клетку (x ₁=80) и аналогично заполняем следующие клетки. В резуль­тате оказываются заполненными следующие клетки:

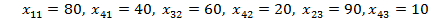
Теперь мы приходим к другому опорному плану. Общий объем перевозок для этого плана составит:

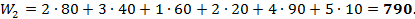
в) Уточнение опорного плана

 

На основании полученного базисного решения выполним уточнение опорного плана по следующему алгоритму:

 

1) Составляем матрицу потенциалов , :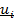

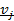· записываем в клетки с заполненными объемами таблицы 3, соответствующие им тарифы, которые будут считаться базовыми (см. таблицу 4):

 

Таблица 4

Матрица потенциалов

	2

 

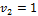
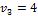
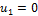
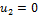
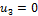
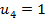
· остальные клетки матрицы и значения самих потенциалов 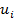, 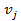определяем, исходя из правила: цифра в клетке есть сумма потенциалов соответствующей строки и столбца, значение 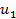принимаем равным нулю;

2) Составляем матрицу разностей:

· из исходных тарифов (см.таблицу 3) вычитаем значения потенциалов в соответствующих клетках (см.таблицу 4) и получаем таблицу 5:

Таблица 5

Матрица разностей

		-1
		-1

· если все элементы в матрице разностей неотрицательные, то данный план перевозок является наилучшим, и решение на этом заканчивается;

· если данное условие не выполнено, то выбирается клетка с наименьшим отрицательным элементом (если наименьших отрицательных элементов в матрице более одного, то из них выбирается тот, который соответствует меньшему значению исходного тарифа, если и тарифы у них одинаковы - выбирается любой из этих элементов);

3) Составляем новый план перевозок:

· в выбранную клетку записываем некоторую вспомогательную переменную t (t > 0 ) и выравниваем суммы по строкам и столбцам (см.таблицу 6):

 

Таблица 6

80- t		t
40+ t		10- t

 

· значение t выбирается таким образом, чтобы одна из заполненных клеток таблицы 6 стала равной нулю, а остальные остались бы положительными, т.е. t =10;

· корректируем план перевозок и определяем новый объем (см.таблицу 7):

 

Таблица 7

 

 

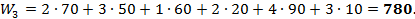
4) Проверяем, является ли полученный план наилучшим:

Таблица 8

Матрица потенциалов

	2	1	3

 

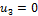
Таблица 9

Матрица разностей

Полученный план перевозок является наилучшим.

 

Решить следующие задачи самостоятельно:

Таблица 10

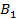
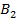
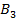
				Объемы
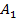
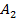
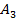
Потребности

Ответ: 1390

Таблица 11

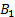
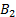
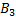
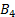
					Объемы
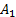
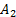
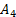
Потребности

Ответ: 875

 

⇐ Предыдущая12345Следующая ⇒

---

Не нашли, что искали? Воспользуйтесь поиском: