
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Төртбұрыштар ауданы.
Пифагор теоремасы-
18-билет
1 .Төртбұрыш туралы түсініктер.
Төртбұрыштар ауданы.
3.Дөңгелек және шеңбер. Шеңбер циркульдің көмегімен салынады. Егер циркуль ашасының бір ұшын О нүктесіне қойып, қарындаш салынған екінші ұшын О нүктесінен айналдырсақ, онда шыққан тұйық сызық шеңбер деп аталады. О нүктесін шеңбер центрі деп атайды. Шеңбердің кез-келген нүктесін центрмен қосатын кесінді шеңбердің радиусы деп аталады. Шеңбердің центрі арқылы өтіп, оның екі нуктесін қосатын кесінді диаметр деп аталады. Дөңгелек шеңбермен шектелген. Дөңгелектің барлық нүктелері оның центрінен дөңгелекті шектейтін шеңбердің радиусына тең немесе одан кіші аралықта орналасқан.
19-билет
1.Жазықтықтағы геометриялық фигуралар және олардың қасиеттері.
2.Арифметикалық прогрессиялар-1-реттік арифметикалық қатар — әрбір келесі саны (2-саннан бастап) алдыңғысына бір тұрақты d санын қосқанда шығатын сандар тізбегі.
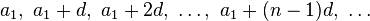
d саны арифметикалық прогрессияның айырмасы деп аталады. Сонымен әрбір арифметикалық прогрессия мына түрде жазылады:
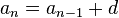
Арифметикалық прогрессияның жалпы мүшесі

формуласымен өрнектеледі. Арифметикалық прогрессияның жалпы мүшесінің тағы бір қасиеті мынадай:. Егер d>0 болса, онда арифметикалық прогрессия өспелі, егер d<0 болса, онда кемімелі болады. Арифметикалық прогрессияның ең қарапайым мысалына натурал сандар тізбегі жатады. Арифметикалық прогрессия мүшелерінің саны шектелген не шектелмеген болуы мүмкін. Арифметикалық прогрессияның алғашқы n мүшесінің қосындысы
 формуласы арқылы есептеледі.
формуласы арқылы есептеледі.
3.Геометриялық прогрессия — әрбір мүшесі (екіншісінен бастап) алдыңғы мүшесінен қандай да бір еселік деп аталатын тұрақты санға (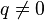 ) көбейтуден шығатын сан қатары:
) көбейтуден шығатын сан қатары:  . Геометриялық Прогрессия q>1 болса, өспелі Геометриялық Прогрессия, 0<q<1 болса, кемімелі Геометриялық Прогрессия, ал q<0 болса, ауыспа таңбалы Геометриялық Прогрессия деп аталады. Геометриялық Прогрессияның кез келген мүшесі (bk) бірінші мүшесі (b1) мен еселігі (q) арқылы мына формуладан табылады::
. Геометриялық Прогрессия q>1 болса, өспелі Геометриялық Прогрессия, 0<q<1 болса, кемімелі Геометриялық Прогрессия, ал q<0 болса, ауыспа таңбалы Геометриялық Прогрессия деп аталады. Геометриялық Прогрессияның кез келген мүшесі (bk) бірінші мүшесі (b1) мен еселігі (q) арқылы мына формуладан табылады::  . Ал Геометриялық Прогрессияның (еселігі 1-ге тең емес) алғашқы n мүшесінің қосындысы (Sn) мына формула бойынша анықталады:
. Ал Геометриялық Прогрессияның (еселігі 1-ге тең емес) алғашқы n мүшесінің қосындысы (Sn) мына формула бойынша анықталады:
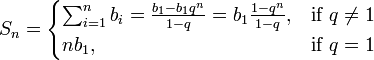
Егер |q|<1 болса, және мүше саны (n) шексіз өссе, онда Sn қосындысы шегіне ұмтылады. Осы S саны шексіз кемімелі геометриялық прогрессияның қосындысы деп аталады. а1+а1q+...+а1qn+... (|q|<1 болғанда) өрнегі геометриялық қатар деп аталатын жинақты қатардың қарапайым мысалы болып есептеледі. Мұндай геометриялық қатардың қосындысы мынаған тең:
Егер.
20-билет
1 .Тригонометрия элементтері-
2.Тригонометриялық формулалар-келтіру, қосу, қос бұрыштың формулалары, тригонометриялық тепе-теңдік болып бөлінеді. Қосу формулалары; 
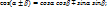
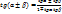
Қос бұрыштың формулалары; 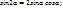


Tригонометриялық тепе-теңдік; 
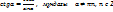
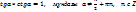
3.Тригонометриялық теңдеулер-айнымалысы тригонометриялық функция таңбасының ішінде болатын теңдеу. Кейбір тригонеметриялық теңдеулердің ерекше атауы бар. 
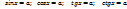 (мұндағы
(мұндағы  саны кез келген нақты сан, яғни
саны кез келген нақты сан, яғни  ) түрінде берілген теңдеулерді қарапайым тригонометриялық теңдеулер деп атайды.
) түрінде берілген теңдеулерді қарапайым тригонометриялық теңдеулер деп атайды.
| <== предыдущая лекция | | | следующая лекция ==> |
| Раздел 5. Бухгалтерский учет | | |
Не нашли, что искали? Воспользуйтесь поиском: