Перетворювач координат

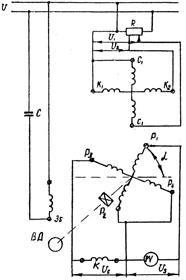
Рис. 17.6. Схема для вирішення прямокутного трикутника

За допомогою поворотних трансформаторів здійснюється перетворення координат на площині (від декартової системи до полярної; від однієї декартової системи до іншої, яка повернута на певний кут α, та низку інших перетворень), визначення гіпотенузи прямокутного трикутника та одного з гострих кутів за двома катетами.

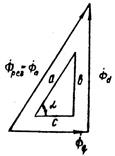
Рис. 17.7. Заданий прямокутний трикутник

Схема для вирішення прямокутного трикутника наведена на рис.17.6. На схемі наведено механічне з’єднання роторів поворотного трансформатора та виконавчого двигуна з амплітудно-фазовим керуванням через редуктор.

Будемо вважати, що задано прямокутний трикутник, який має сторони з довжинами а, b, с (рис.17.7).

Відомі катети b і с. потрібно визначити гіпотенузу а й кут α.

Довжини катетів задаємо за допомогою подільника R (рис.17.6) у вигляді напруг:

, (17.66)

. (17.67)

МРС головної та компенсаційної обмоток створюють пульсуючий магнітні потоки та , осі яких нерухомі у просторі. Якщо машина не насичена, то модулі та пропорційні до напруг 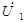та . Додаючись, потоки та створюють результуючий магнітний потік 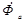, вектор якого створює за осями головної й компенсаційної обмоток такі ж кути, як і гіпотенуза а з катетами b та с. Подовжня та поперечна складові результуючого потоку наближено дорівнюють:

; (17.68)

. (17.69)

Результуючий потік дорівнює:

. (17.70)

Цей потік наводить в роторних обмотках ЕРС:

; (17.71)

. (17.72)

Припустимо, що в початковий момент часу (до вмикання та ) α=0, тобто осі обмоток Р₃-Р₄ та С₁-С₂ співпадають (рис.17.6). При подачі напруг та потік наведе в обмотках ротора ЕРС у відповідності з (17.71), (17.72). Виконавчий двигун почне обертатись, і його обертання буде продовжуватись до того моменту часу, доки на затискачах обмотки керування «К» буде напруга, тобто до тих пір, доки обмотка Р₃-Р₄ не займе положення, при якому її вісь буде перпендикулярною до осі магнітного потоку . Тому ротор повернеться на кут α. При цьому:

; .

Нехтуючи спадом напруги в обмотці, можливо записати:

. (17.73)

Таким чином, гіпотенуза а пропорційна напрузі при нерухомому роторі, а кут α дорівнює одному з гострих кутів прямокутного трикутника.

Рис. 17.8. Схема вмикання перетворювача координат

За допомогою поворотного трансформатора можливо перетворювати одну систему координат в іншу, повернуту на деякий кут α. Для цього суміщують вихідну систему координат з осями обмоток статора, а перетворену – з осями обмоток ротора (рис.17.8).

При вмиканні обмоток С₁-С₂ та К₁-К₂ на синфазні напруги 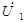та створюються магнітні потоки за співвідношеннями (17.68), (17.69). У вторинних обмотках кожен з цих потоків наводить відповідну ЕРС:

; (17.74)

. (17.75)

Складові ЕРС у (17.74), (17.75) дорівнюють:

; (17.76)

. (17.77)

; (17.78)

. (17.79)

Підставляючи з (17.76)÷(17.79) у (17.74), (17.75) з урахуванням (17.68), (17.69) одержимо, вважаючи ; :

; (17.80)

; (17.81)

Формули (17.80), (17.81) відповідні співвідношенням між координатами повернутих осей у декартовій системі. Якщо

, (17.82)

. (17.83)

то

, (17.84)

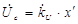. (17.85)

Оскільки за схемою рис.17.6 визначається довжина гіпотенузи прямокутного трикутника й кут α за двома катетами, це відповідно переходу від декартової системи координат (катети) до полярної (гіпотенуза й кут).

В цьому режимі, як і в попередніх, здійснюється симетрування:

а) первинне при z₁=z_к; z_s≠z_c;

б) вторинне при z_s=z_c; z₁≠z_к;

в) первинне та вторинне при z₁=z_к; z_s=z_c;

При первинному симетруванні перетворювача координат 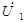та , які співпадають за фазою, повинні бути задані в одних масштабах. При вторинному симетруванні – навпаки. Найзручнішим видом симетрування є сукупне первинне та вторинне.

Не нашли, что искали? Воспользуйтесь поиском: