Тема: Обработка результатов эксперимента

Лабораторная работа № 8

Цель работы: Изучение возможностей пакета Ms Excel при решении задач обработки экспериментальных данных. Приобретение навыков обработки результатов эксперимента.

Одной из распространенных задач в науке, технике, экономике является аппроксимация экспериментальных данных, алгебраических данных аналитическими выражениями. Возможность подобрать параметры уравнения таким образом, чтобы его решение совпало с данными эксперимента, зачастую является доказательством (или опровержением) теории.

Рассмотрим следующую математическую задачу. Известные значения некоторой функции f образуют таблицу:

Таблица 8.1

Необходимо построить аналитическую зависимость y=f(x), наиболее близко описывающую результаты эксперимента. Построим функцию y=f(x, a₀ a₁,..., a_k) таким образом, чтобы сумма квадратов отклонений измеренных значений y_i от расчетных f(x_i,a₀, a₁,..., a_k) была наименьшей (см. рис. 8.1).

Рис. 8.1

Математически эта задача равносильна следующей: найти значение параметров a₀, a₁, a₂,...,a_k при которых функция принимала минимальное значение.

8.1)

Эта задача сводится к решению системы уравнений:

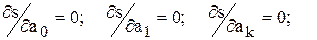(8.2)

Если параметры a_i входят в зависимость y=f(x,a_o,a₁, …, a_k) линейно, то мы получим систему линейных уравнений:

(8.3)

Решив систему (8.3), найдем параметры a_o, a₁,..., a_k и получим зависимость y = f(x, a_o, a₁,..., a_k).

Не нашли, что искали? Воспользуйтесь поиском: