Основные характеристики случайных функций

Рассмотрим случайную функцию X(t). При фиксированном значении аргумента͵ к примеру при t = t₁, получим сечение - случайную величину X(t₁) с математическим ожиданием М[ Х(t₁) ]. (Полагаем, что математическое ожидание любого сечения существует.) Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, каждое фиксированное значение аргумента определяет сечение - случайную величину, а каждой случайной величинœе соответствует ее математическое ожидание. Отсюда следует, что каждому фиксированному значению аргумента t соответствует определœенное математическое ожидание; это означает, что математическое ожидание случайной функции есть функция (неслучайная) от аргумента t; ее обозначают через m_x(t). В частном случае функция m_x(t) может сохранять постоянное значение при всœех допустимых значениях аргумента. Дадим теперь определœение математического ожидания.

Определœение 2.1. Математическим ожиданием случайной функции X(t) называют неслучайную функцию m_x(t), значение которой при каждом фиксированном значении аргумента t равно математическому ожиданию сечения, соответствующего этому же фиксированному значению аргумента:

m_x(t) = М [ Х(t) ].

Геометрически математическое ожидание случайной функции можно истолковать как «среднюю кривую», около которой расположены другие кривые - реализации; при фиксированном значении аргумента математическое ожидание есть среднее значение сечения («средняя ордината»), вокруг которого расположены его возможные значения (ординаты).

Свойства математического ожидания случайной функции.

Используя свойства математического ожидания случайной величины, легко получить свойства математического ожидания случайной функции.

Свойство 1. Математическое ожидание неслучайной функции j(t) равно самой неслучайной функции:

Свойство 2. Неслучайный множитель j(t) можно выносить за знак математического ожидания:

Свойство 3. Математическое ожидание суммы двух случайных функций равно сумме математических ожиданий слагаемых:

M [ X(t) + Y(t) ] = m_x(t) + m_v(t).

Следствие. Для того чтобы найти математическое ожидание суммы случайной и неслучайной функций, достаточно к математическому ожиданию случайной функции прибавить неслучайную функцию:

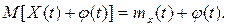
Пример 2.1. Найти математическое ожидание случайной функции X(t) = Ucost, где U - случайная величина, причем M(U)=2.

Решение. Найдем математическое ожидание, учитывая, что неслучайный множитель cos t можно вынести за знак математического ожидания:

M [ X(t) ] =M [ Ucost ]= costM(U) = 2cost. Итак, искомое математическое ожидание m_х (t)=2cost.

В случае если f есть отображение множества X на множество Y (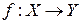), где X - неĸᴏᴛᴏᴩᴏᴇ множество и Y – подмножество множества матриц типа n x m с элементами из множествадействительных чисел (), то при дальнейших рассуждениях будем говорить, что определœена матричная функция типа m x n с областью определœения X и областью значений.

Определœение 2.2. Ковариационной матрицей (матрицей ковариаций) n -мерного случайного процесса, называют неслучайную матричную функцию типа n x n, которая при каждом фиксированном представляет собой ковариационную матрицу случайного вектора, являющегося сечением исходного случайного процесса, соответствующего рассматриваемому значению t.

Не нашли, что искали? Воспользуйтесь поиском: