ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Правильный ответ 2.
Электричество и магнетизм 3 Магнитостатика
3.3.1-1
| Относительно статических магнитных полей справедливы утверждения: | 1: Силовые линии магнитного поля являются замкнутыми. * 2: Магнитное поле не совершает работы над движущимися электрическими зарядами. * 3: Статические магнитные поля являются потенциальными. |
Ответы: 1, 2
3.3.1-2
| Относительно статических магнитных полей справедливы утверждения: | 1: Магнитное поле действует только на движущиеся электрические заряды. * 2: Магнитное поле является вихревым. * 3: Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность отличен от нуля. |
Ответы: 1, 2
3.3.1-3
| Относительно статических магнитных полей справедливы утверждения: | 1: Магнитное поле действует на заряженную частицу с силой, пропорциональной скорости частицы. * 2: Циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура определяется токами, охватываемыми этим контуром. * 3: Силовые линии магнитного поля разомкнуты. |
Ответы: 1, 2
3.3.2-1
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем J1=2J2. Индукция  магнитного поля равна нулю в некоторой точке интервала….
| 1: b 2: a 3: d * 4: c |
Для нахождения индукции 
результирующего магнитного поля в некоторой точке необходимо воспользоваться принципом суперпозиции магнитных полей. Для этого определяются направления магнитных индукций 
и 
2-х полей, создаваемых каждым проводником с током в отдельности, и вектор находится геометрически: 
.
Правило нахождения направления вектора в данной точке поля: через эту точку проводится силовая линия магнитного поля (окружность). Вектор направлен по касательной к силовой линии в данной точке. Направление магнитной силовой линии, а значит, и вектора определяется по правилу правого винта: если большой палец правой руки расположить по направлению тока, то направление обхвата проводника четырьмя пальцами покажет направление линий магнитной индукции.
и 
определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током: 
, 
. Для того, чтобы индукция результирующего магнитного поля в некоторой точке равнялась нулю, векторы и в этой точке должны быть равными по модулю и противоположными по направлению.
В данной задаче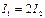 
. Следовательно, B1=B2 при r 1=2 r 2.
Этому условию соответствуют 2 точки: A и D.
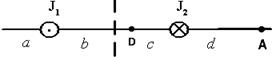
Но в точке D векторы и сонаправлены, а в точке A направлены противоположно.
Т.о., вектор равен нулю в некоторой точке интервала d.
Ответ: 3
3.3.2-2
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем J2=2J1. Индукция  магнитного поля равна нулю в некоторой точке участка….
| 1: a * 2: b 3: c 4: d |
В данной задаче 
. Следовательно, B1=B2 при r 2=2 r 1. Этому условию соответствуют 2 точки: A и D. 
. Но в точке D векторы и сонаправлены, а в точке A направлены противоположно. 
Т.о., вектор равен нулю в некоторой точке интервала 
.
Ответ: 1
3.3.2-3
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем J2=2J1. Индукция  магнитного поля равна нулю в некоторой точке участка….
| 1: a * 2: d 3: b 4: c |
В данной задаче . Следовательно, B1=B2 при r 2=2 r 1. Этому условию соответствуют 2 точки: A и D. 
. Но в точке D векторы и сонаправлены, а в точке A направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала 
.
Ответ: 1
3.3.2-4
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем J1=2 J2. Индукция  магнитного поля равна нулю в некоторой точке участка….
| 1: c * 2: a 3: b 4: d |
В данной задаче 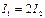. Следовательно, B1=B2 при r 1=2 r 2. Этому условию соответствуют 2 точки: A и D. 
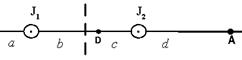. Но в точке A векторы и сонаправлены, а в точке D направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала 
.
Ответ: 1
3.3.2-5
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем J2=2J1. Индукция  магнитного поля равна нулю в некоторой точке участка….
| 1: b * 2: a 3: c 4: d |
В данной задаче . Следовательно, B1=B2 при r 2=2 r 1. Этому условию соответствуют 2 точки: A и D. 
. Но в точке A векторы и сонаправлены, а в точке D направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала 
.
Ответ: 1
3.3.2-6
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем J1=2J2. Индукция  магнитного поля равна нулю в некоторой точке участка….
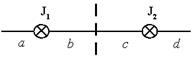
| 1: c * 2: a 3: b 4: d |
В данной задаче 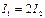. Следовательно, B1=B2 при r 1=2 r 2. Этому условию соответствуют 2 точки: A и D. 
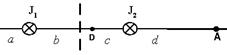. Но в точке A векторы и сонаправлены, а в точке D направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала .
Ответ: 1
3.3.2-7
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем J2=2J1. Индукция  магнитного поля равна нулю в некоторой точке участка….
| 1: a * 2: b 3: c 4: d |
В данной задаче . Следовательно, B1=B2 при r 2=2 r 1. Этому условию соответствуют 2 точки: A и D.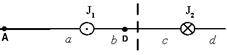 
. Но в точке D векторы и сонаправлены, а в точке A направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала .
Ответ: 1
3.3.2-8
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем J2=2J1. Индукция магнитного поля равна нулю в некоторой точке участка….
| 1: a * 2: d 3: b 4: c |
В данной задаче . Следовательно, B1=B2 при r 2=2 r 1. Этому условию соответствуют 2 точки: A и D. 
. Но в точке D векторы и сонаправлены, а в точке A направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала .
Ответ: 1
3.3.2-9
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем J1=2J2. Индукция  магнитного поля равна нулю в некоторой точке участка….
| 1: c * 2: a 3: b 4: d |
В данной задаче 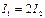. Следовательно, B1=B2 при r 1=2 r 2. Этому условию соответствуют 2 точки: A и D. 
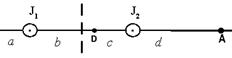. Но в точке A векторы и сонаправлены, а в точке D направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала .
Ответ: 1
3.3.2-10
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем J2=2J1. Индукция  магнитного поля равна нулю в некоторой точке участка….
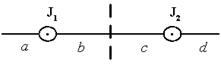
| 1: b * 2: a 3: c 4: d |
В данной задаче . Следовательно, B1=B2 при r 2=2 r 1. Этому условию соответствуют 2 точки: A и D. 
. Но в точке A векторы и сонаправлены, а в точке D направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала .
Ответ: 1
3.3.2-11
На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем J1=2J2. Индукция магнитного поля равна нулю в некоторой точке участка….
| 1: c * 2: a 3: b 4: d |
В данной задаче 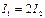. Следовательно, B1=B2 при r 1=2 r 2. Этому условию соответствуют 2 точки: A и D. 
. Но в точке A векторы и сонаправлены, а в точке D направлены противоположно. Т.о., вектор равен нулю в некоторой точке интервала .
Ответ: 1
3.3.2-12
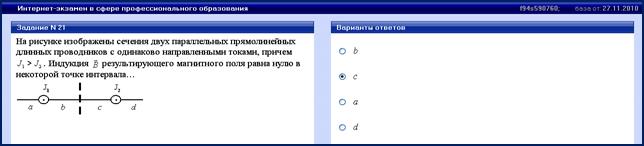
Правильный ответ 2.
3.3.3-1
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I1=2I2, то вектор  индукции результирующего поля в точке А направлен…
| 1: вниз* 2: вверх 3: вправо 4: влево |
Для нахождения магнитной индукции в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций и 2-х полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: . Правило нахождения направления вектора в данной точке поля: через эту точку проводится силовая линия магнитного поля (окружность). Вектор направлен по касательной к силовой линии в данной точке. Направление магнитной силовой линии, а значит, и вектора определяется по правилу правого винта: если большой палец правой руки расположить по направлению тока, то направление обхвата проводника четырьмя пальцами покажет направление линий магнитной индукции. и определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током: , . В данной задаче 
и 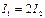. Отсюда: 
. Т.о., результирующий вектор направлен вниз.
Ответ: 1
3.3.3-2
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I1=2I2, то вектор  индукции результирующего поля в точке А направлен…
| 1: вниз* 2: вверх 3: вправо 4: влево |
, . В данной задаче 
, .
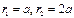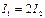Отсюда: 
. Т.о., результирующий вектор направлен вниз.
Ответ: 1
3.3.3-3
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I1=2I2, то вектор  индукции результирующего поля в точке А направлен…
| 1: вверх* 2: вниз 3: вправо 4: влево |
, . В данной задаче , .
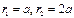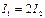Отсюда: . Т.о., результирующий вектор направлен вверх.
Ответ: 1
3.3.3-4
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I2=2I1, то вектор  индукции результирующего поля в точке А направлен…
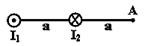
| 1: вниз* 2: вверх 3: вправо 4: влево |
, . В данной задаче 
, 
.
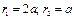Отсюда: 
. Т.о., результирующий вектор направлен вниз.
Ответ: 1
3.3.3-5
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I2=2I1, то вектор индукции результирующего поля в точке А направлен…
| 1: вверх* 2: вниз 3: вправо 4: влево |
, . В данной задаче , .
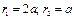Отсюда: . Т.о., результирующий вектор направлен вверх.
Ответ: 1
3.3.3-6
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I1=2I2, то вектор индукции результирующего поля в точке А направлен…
| 1: влево 2: вверх* 3: вниз 4: вправо |
, . В данной задаче 
, 
.
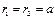Отсюда: 
. Т.о., результирующий вектор направлен вверх.
Ответ: 2
3.3.4-1
В однородном магнитном поле на горизонтальный проводник с током, направленным вправо, действует сила Ампера, направленная перпендикулярно плоскости рисунка от наблюдателя. При этом линии магнитной индукции поля направлены …
| 1. вправо 2. влево 3. вниз* 4. вверх |
Правило левой руки: если расположить ладонь левой руки так, что В входили в ладонь, а 4 вытянутых пальца совпадали с направлением тока, то отставленный большой палец укажет направление силы Ампера
Ответ: 3
3.3.5-1
Траектория движения протона в однородном магнитном поле представляет собой окружность, расположенную в плоскости рисунка. Если протон вращается по часовой стрелке, то линии магнитной индукции поля направлены …
| 1. 
2.  *
3. 
4. 
|
Скорость по касательной, сила к центру, заряд положительный,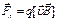 
. Вектор индукции магнитного поля направлен к нам.
Ответ: 2
3.3.6-1
На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы 1 …
| 1: q = 0 2: q > 0 3: q < 0* |
Сила Лоренца 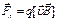. Используя определение направления векторного произведения, с учётом указанных на рисунке направлений векторов скорости и индукции магнитного поля заряд частицы 1 должен быть отрицательным.
Ответ: 3
3.3.6-2
На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы 2 …
| 1: q = 0* 2: q > 0 3: q < 0 |
Сила Лоренца 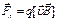. Поскольку движение частицы 2 не изменяется (траектория прямолинейная), то сила Лоренца, действующая на частицу 2 равна нулю. Поскольку скорость и индукция магнитного поля не равны нулю, то причина равенства нулю сила Лоренца заключена в равенстве нулю заряда частицы 2.
Ответ: 1
3.3.6-3
На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы 3 …
| 1: q > 0* 2: q = 0 3: q < 0 |
Сила Лоренца 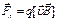. Используя определение направления векторного произведения, с учётом указанных на рисунке направлений векторов скорости и индукции магнитного поля заряд частицы 3 должен быть положительным.
Ответ: 1
3.3.6-4
На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы 1 …
| 1: q > 0* 2: q = 0 3: q < 0 |
Сила Лоренца 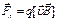. Используя определение направления векторного произведения, с учётом указанных на рисунке направлений векторов скорости и индукции магнитного поля заряд частицы 1 должен быть положительным.
Ответ: 1
3.3.6-5
На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы 3 …
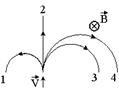
| 1:q < 0* 2:q > 0 3:q = 0 |
Сила Лоренца 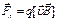. Используя определение направления векторного произведения, с учётом указанных на рисунке направлений векторов скорости и индукции магнитного поля заряд частицы 3 должен быть отрицательным.
Ответ: 1
3.3.6-6
Не нашли, что искали? Воспользуйтесь поиском: