КЛЮЧЕВЫЕ ОПЕРАЦИИ ЦИФРОВОЙ ОБРАБОТКИ

Существуют многочисленные алгоритмы ЦОС как общего типа для сигналов в их классической временной форме (телекоммуникации, связь, телевидение и пр.), так и специализированные в самых различных отраслях науки и техники (геоинформатике, геологии и геофизике, медицине, биологии, военном деле, и пр.). Все эти алгоритмы, как правило – блочного типа, построенные на комбинациях достаточно небольшого набора типовых цифровых операций, к основным из которых относятся свертка, корреляция, фильтрация, функциональные преобразования, модуляция.

Линейная свертка – основная операция ЦОС, особенно в режиме реального времени. Для двух конечных последовательностей h(n) и x(n) свертка определяется выражением:

или (1.9)

Часто используют частный случай формулы свертки:

(1.9а)

где: _* - символьное обозначения операции свертки. Как правило, в системах обработки одна из последовательностей x(n) представляет собой обрабатываемые данные (сигнал на входе системы), вторая h(n) – оператор (импульсная характеристика) системы, а функция y(n) – выходной сигнал системы. В компьютерных системах с памятью для входных данных оператор h(n) может быть двусторонним от –N₁ до +N₂, например – симметричным h(-n) = h(n), с соответствующим изменением пределов суммирования в (1.9а), что позволяет получать выходные данные без сдвига относительно входных. Пример выполнения свертки приведен на рис. 1.4.

Рис. 1.4. Примеры дискретной свертки

Преобразование свертки однозначно определяет выходной сигнал для установленных значений входного сигнала при известном импульсном отклике системы.

Корреляция существует в двух формах: автокорреляции и взаимной корреляции.

Взаимно-корреляционная функция (ВКФ, cross-correlation function - CCF), и ее частный случай для центрированных сигналов функция взаимной ковариации (ФВК) – это показатель степени сходства формы и свойств двух сигналов. Таким образом, ВКФ показывает степень сходства для сдвинутых экземпляров двух разных сигналов и для аналоговых сигналов имеет следующий вид вид:

(1.10)

Для двух дискретных последовательностей x(k) и y(k) длиной К с нулевыми средними значениями оценка взаимной ковариации может быть выполнена по формулам:

K_xy(n) = (1/(K-n+1)) x(k) y(k+n), n = 0, 1, 2, … (1.11)

K_xy(n) = (1/(K-n+1)) x(k-n) y(k), n = 0, -1, -2, … (1.11')

Рис. 1.5. Функция взаимной ковариации двух детерминированных сигналов

Пример определения сдвига между двумя детерминированными сигналами, представленными радиоимпульсами, по максимуму ФВК приведен на рис. 1.5. По максимуму ФВК может определяться и сдвиг между сигналами, достаточно различными по форме.

На рис. 1.6 приведен аналогичный пример ФВК двух одинаковых по форме сигналов, на один из которых наложен шумовой сигнал. Мощность шума превышает мощность сигнала. Вычисление ФВК на рисунке выполнено в двух вариантах. Вариант 1 полностью соответствует формуле (1.11). Но в условиях присутствия в сигналах достаточно мощных шумов вычисление ФВК обычно выполняется по варианту 2 – с постоянным нормировочным множителем

Рис. 1.6. ФВК двух сигналов, один из которых сильно зашумлен.

На рис. 1.7 приведен пример вычисления функции взаимной ковариации двух одинаковых сигналов, скрытых в шумах. ФВК позволяет не только определить величину сдвига между сигналами, но и уверенно оценить период колебаний в исследуемых радиоимпульсах.

Рис. 1.7. ФВК двух зашумленных радиоимпульсов.

Автокорреляционная функция (АКФ, correlation function, CF) является количественной интегральной характеристикой формы сигнала, дает информацию о структуре сигнала и его динамике во времени. Она, по существу, является частным случаем ВКФ для одного сигнала и представляет собой скалярное произведение сигнала и его копии в функциональной зависимости от переменной величины значения сдвига:

B_x(n) = (1/(K-n+1)) x(k) x(k+n), n = 0, 1, 2, … (1.12)

АКФ имеет максимальное значение при n=0 (умножение сигнала на самого себя), является четной функцией B_xy(-n)=B_xy(n), и значения АКФ для отрицательных координат обычно не вычисляются. АКФ центрированного сигнала K_x(n) представляет собой функцию автоковариации.

Рис. 1.8. Автокорреляционные функции.

В качестве примера на рис. 1.8 приведены два сигнала – прямоугольный импульс и радиоимпульс одинаковой длительности Т, и соответствующие данным сигналам формы их АКФ. Амплитуда колебаний радиоимпульса установлена равной амплитуды прямоугольного импульса, при этом энергии сигналов будут одинаковыми, что подтверждается равными значениями максимумов АКФ. При конечной длительности импульсов длительности АКФ также конечны, и равны удвоенным значениям длительности импульсов (при сдвиге копии конечного импульса на интервал его длительности как влево, так и вправо, произведение импульса со своей копией становится равным нулю). Частота колебаний АКФ радиоимпульса равна частоте колебаний заполнения радиоимпульса (боковые минимумы и максимумы АКФ возникают каждый раз при последовательных сдвигах копии радиоимпульса на половину периода колебаний его заполнения).

Линейная цифровая фильтрация является одной из операций ЦОС, имеющих первостепенное значение. Она может определяться как

(1.13)

Реализацией этого соотношения является структурная схема фильтра, представленного на рис. 1.9. Как видно, она соответствует прямому порядку выполнения сложений и умножений.

Рис. 1.9. Прямая форма трансверсального фильтра

Такую структуру из-за сходства с линией задержки с отводами иногда называют фильтром с многоотводной линией задержки или трансверсальным фильтром (z^-1 – задержка на один интервал дискретизации).

При описании фильтра в виде линейного разностного уравнения N -го порядка с постоянными коэффициентами, имеющего вид:

(1.14)

следует, что для построения цифрового фильтра необходимо иметь настоящие и предыдущие значения выходной, входной и промежуточной последовательностей. Это подразумевает необходимость задержки или запоминания этих величин. Наряду с этим следует обеспечить умножение задержанных выборок на коэффициенты и суммирование полученных результатов.

Цифровой фильтр может быть построен либо на базе регистра памяти, арифметического устройства и устройства управления вычислительной машины, либо в виде специализированного цифрового устройства. В первом случае структура фильтра может рассматриваться как детализация расчетного алгоритма, на основе которого строится программа. Во втором случае ее удобно представлять в виде конкретной схемы специализированного устройства. Текущий отчет отклика определяется текущим и предшествующим значениями входной последовательности .

Выходная последовательность фильтра должна обязательно зависеть хотя бы от одного отсчета входной последовательности. Кроме того, текущий отчет отклика может зависеть и от своих же отсчетов, задержанных на определенное число временных отсчетов, т.е. предшествующих отсчетов отклика. В зависимости от наличия или отсутствия этой зависимости фильтры делятся на:

- рекурсивные (БИХ- фильтры);

- нерекурсивные (КИХ- фильтры).

Для рекурсивных фильтров соотношение между входной последовательностью 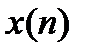и откликом фильтра 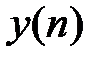записывается следующим образом:

В нерекурсивных фильтрах связь между входной последовательностью и откликом имеет вид:

Разностное уравнение для рекурсивных фильтров, показывающее связь между входной последовательностью 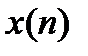и откликом фильтра , записывается следующим образом:

, (1.15)

То есть передаточная характеристика равна:

, где . (1.16)

Корни числителя называются нулями фильтра, корни знаменателя – полюсами.

Так как , то выражение (1.15) можно записать в виде:

(1.17)

Поскольку это разностное уравнение может быть записано непосредственно из выражения для передаточной функции, то форму построения цепи соответствующей этому разностному уравнению называют прямой формой 1.

Простая структура реализации данного разностного уравнения показана на рис. 1.10.

Рис.1.10. Прямая форма (direct form I)

Здесь z^-1 – элементы памяти, осуществляющие задержку дискретной последовательности на 1 такт (согласно свойствам z-преобразования это соответствует умножению z-преобразования на z^-1), т.к. некоторое количество предыдущих отсчетов входного сигнала хранится в ячейках памяти, которые образуют дискретную линию задержки.

b_i и a_i – вещественные коэффициенты, на которые умножаются отсчеты.

К основным операциям фильтрации сигнала относят операции сглаживания, прогнозирования, дифференцирования, интегрирования и разделения сигналов, а также выделение информационных (полезных) сигналов и подавление шумов (помех). Основными методами цифровой фильтрации данных являются частотная селекция сигналов и оптимальная (адаптивная) фильтрация.

Дискретные преобразования позволяют описывать сигналы с дискретным временем в частотных координатах или переходить от описания во временной области к описанию в частотной. Переход от временных (пространственных) координат к частотным необходим во многих приложениях обработки данных.

Самым распространенным преобразованием является дискретное преобразование Фурье.

(1.18)

Существует и обратное дискретное преобразование Фурье. Переход от дискретного спектра к временным отсчетам сигнала выражается следующей формулой:

(1.19)

Это выражение отличается от формулы прямого ДПФ (1.18) лишь знаком в показателе комплексной экспоненты и наличием множителя 1/ N перед оператором суммирования.

Алгоритм быстрого преобразования Фурье

Для вычисления одного коэффициента ДПФ по формуле (1.18) необходимо выполнить N комплексных умножений и сложений. Таким образом, расчет всего ДПФ, содержащего N коэффициентов, потребует пар операций «умножение ̶ сложение». Число операций возрастает пропорционально квадрату размерности ДПФ. Однако, если N не является простым числом и может быть разложено на множители, процесс вычислений можно ускорить, разделив анализируемый набор отсчетов на части, вычислив их ДПФ и объединив результаты. Такие способы вычисления ДПФ называются быстрым преобразованием Фурье (БПФ; английский термин — Fast Fourier Transform, FFT) и повсеместно используются на практике.

При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени либо по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).

Модуляция сигналов. Системы регистрации, обработки, интерпретации, хранения и использования информационных данных становятся все более распределенными, что требует коммуникации данных по высокочастотным каналам связи. Как правило, информационные сигналы являются низкочастотными и ограниченными по ширине спектра, в отличие от широкополосных высокочастотных каналов связи, рассчитанных на передачу сигналов от множества источников одновременно с частотным разделением каналов. Перенос спектра сигналов из низкочастотной области в выделенную для их передачи область высоких частот выполняется операцией модуляции. При модуляции значения информационного (модулирующего) сигнала переносятся на определенный параметр высокочастотного (несущего) сигнала.

Самые распространенные схемы модуляции для передачи цифровой информации по широкополосным каналам – это амплитудная (amplitude shift keying – ASK), фазовая (phase shift keying – PSK) и частотная (frequensy shift keying – FSK) модуляции. При передаче данных по цифровым сетям используется также импульсно-кодовая модуляция (pulse code modulation – PCM).

Не нашли, что искали? Воспользуйтесь поиском: