Явление самоиндукции

Явление самоиндукции является частным случаем явления электромагнитной индукции. Если в некотором контуре протекает электрический ток, то он создает магнитное поле и магнитный поток через поверхность контура. При изменениях тока изменяется магнитный поток, и возникает ЭДС индукции противодействующая этому изменению по правилу Ленца. Ее и называют ЭДС индукции .

Величина индукции магнитного поля, а значит и магнитный поток через его поверхность, пропорциональны протекающему току:

. (20.10)

Коэффициент пропорциональности в формуле (20.10) называется индуктивностью контура. Единицей индуктивности является 1 генри (Гн).

Индуктивность определяется геометрическими параметрами контура и магнитными свойствами окружающей среды. Для того, чтобы более конкретно представить влияние на величину индуктивности этих факторов вычислим индуктивность соленоида, близкого к идеальному, т.е. с длиной 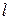, большой по сравнению с геометрическими размерами сечения, имеющего площадь 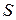(). Индукция магнитного поля соленоида при силе тока в нем

(20.11)

где - количество витков на единицу длины соленоида;

- магнитная проницаемость среды внутри соленоида.

Количество витков в соленоиде , и через каждый из них магнитное поле создает поток

. (20.12)

Потокосцепление (полный поток)

. (20.13)

Очевидно, что индуктивность соленоида выражается соотношением

, (20.14)

где есть объем соленоида.

Если в области действия магнитного поля ферромагнетики отсутствуют, то магнитная проницаемость остается постоянной и ЭДС индукции

. (20.15)

20.5. Токи при замыкании и размыкании цепи с индуктивностью

Влияние самоиндукции на протекание тока в цепи очень наглядно демонстрируется характером изменения тока в цепи, содержащей индуктивность и активное сопротивление при ее подключении и отключении от источника тока. В положении переключателя, показанном на рисунке, в цепи идет ток

. (20.16)

Предположим, что в некоторый момент времени переключатель мгновенно отключает источник тока и замыкает индуктивность на резистор. В отсутствие источника сила тока в цепи начнет убывать, но возникнет ЭДС самоиндукции, которая будет ее поддерживать. Падение напряжения на резисторе должно быть равно ЭДС самоиндукции :

. (20.17)

Разделим на :

(20.18)

Разделим в (20.17) переменные:

(20.19)

После интегрирования получаем:

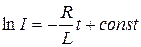. (20.20)

Потенцирование этого соотношения дает зависимость тока от времени:

. (20.21)

При ток равен начальному значению , поэтому и константа равна этому току:

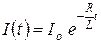. (20.22)

Графически эта зависимость выглядит так, как это показано на рисунке. Решение аналогичного уравнения для нарастания тока в цепи приводит к соотношению

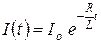. (20.23)

Не нашли, что искали? Воспользуйтесь поиском: