
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методы решения задач линейного программирования
Симплекс-метод
Основным методом решения ЗЛП является симплексный метод. Перед его использованием ЗЛП необходимо привести к канонической форме записи. При этом используются следующие приемы:
1. Для перехода от задачи максимизации к задаче минимизации целевую функцию необходимо умножить на –1.
2. Переменные, на которых не наложено ограничение неотрицатель-ности, заменяются во всех ограничениях и в целевой функции разностью двух неотрицательных переменных
xj = uj- wj uj, wj ³ 0.
3. Переход к ограничениям с неотрицательными правыми частями осуществляется умножением левой и правой частей ограничений с отрицательными правыми частями на –1. При этом знаки соответствующих неравенств меняются на противоположные.
4. Переход от ограничений-неравенств к ограничениям-равенствам производится путем введения дополнительных неотрицательных переменных. При этом если знак неравенства £, дополнительная переменная прибавляется к левой части ограничения, а если ³, то вычитается. Таким образом, ограничение-неравенство
ai1x1 + ai2x2 +…+ ainxn £ bi
преобразуется в ограничение-равенство
ai1x1 + ai2x2 +…+ ainxn + xn+1 = bi (xn+1 ³ 0),
где xn+1 – дополнительная переменная, xn+1³0.
Ограничение-неравенство:
ai1x1 + ai2x2 +…+ ainxn ³ bi
преобразуется в ограничение-равенство следующим образом:
ai1x1 + ai2x2 +…+ ainxn - xn+1 = bi (xn+1 ³ 0)
В каждое ограничение-неравенство вводится своя дополнительная переменная. Число вводимых дополнительных неотрицательных переменных равно числу преобразуемых неравенств.
Рассмотрим ЗЛП в канонической форме:

Вектор X = (x1,…, xn), удовлетворяющий системе ограничений ЗЛП, называется допустимым решением или планом.
План, X*=(x1*,…,xn*), при котором целевая функция принимает оптимальное значение, называется оптимальным.
Перепишем ЗЛП в векторной форме.

где A1,…,An – m-мерные вектор-столбцы, составленные из коэффициентов при переменных в системе ограничений:
 .
.
B – вектор-столбец свободных членов системы ограничений:
 .
.
План X = (x1,…, xn) называется опорным планом ЗЛП, если система векторов Аj, входящих в разложение  с положительными коэффи-циентами xj, линейно независима. Так как векторы Аj являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем m.
с положительными коэффи-циентами xj, линейно независима. Так как векторы Аj являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем m.
Симплексный метод решения ЗЛП основан на переходе от одного опорного плана к другому, при котором значение целевой функции убывает. Указанный переход возможен, если известен какой-нибудь исходный опорный план. Такой план можно легко указать, если ЗЛП записана в форме:

Векторная форма данной задачи имеет вид:

где

Переменные, которые входят только в одно уравнение системы ограничений с коэффициентом равным 1, называют базисными переменными (в рассматриваемом примере это переменные x1… xm). Остальные переменные называются свободными. Тогда, приравнивая базисные переменные соответствующим правым частям ограничений, а свободные переменные нулю, получим опорный план X = (b1, b2,…, bm,0,…,0), определяемый системой единичных векторов, А1,…, Аm, которые образуют базис m-мерного пространства.
Для удобства расчетов в симплексном методе все данные по задаче аносят в симплекс-таблицу:
Таблица 5
| xd | сd | B | с1 | c2 | … | cn | |
| X1 | x2 | … | xn | ||||
| xd1 | cd1 | b1 | A11 | a12 | … | a1n | |
| xd2 | cd2 | b2 | A21 | a22 | … | a2n | |
| … | … | … | … | … | … | … | |
| xdm | cdm | bm | Am1 | am2 | … | amn | |
| F | D1 | D2 | … | Dn | |||
В верхнюю строку таблицы заносятся коэффициенты при всех переменных в целевой функции. В первом столбце таблицы записываются базисные переменные в той последовательности, в которой они входят в систему ограничений, во втором – коэффициенты целевой функции при базисных переменных, в третьем – правые части всех ограничений, в последующих столбцах – коэффициенты при соответствующих переменных в системе ограничений. В нижней строке таблицы записываются оценки по каждой переменной, определяемые следующим образом:  . Очевидно, что для базисных переменных оценки равны нулю.
. Очевидно, что для базисных переменных оценки равны нулю.
На каждой итерации симплекс-метода осуществляется вывод из базиса какой-либо переменной и включение в него другой переменной с соответствующим пересчетом элементов таблицы. Перед решением задачи ее необходимо привести к канонической форме.
Основные шаги симплекс – метода:
1. Определение начального опорного плана.
2. Составление симплекс-таблицы.
3. Вычисление оценок  .
.
4. Анализ оценок.
4.1. Если  , то получено оптимальное решение.
, то получено оптимальное решение.
4.2. Если существует хотя бы одна оценка Dj > 0, для которой  , то целевая функция не ограничена снизу на множестве допустимых решений (ЗЛП не имеет решения).
, то целевая функция не ограничена снизу на множестве допустимых решений (ЗЛП не имеет решения).
4.3. Из всех оценок Dj > 0 выбирается максимальная: 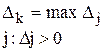
Переменная xk, которой соответствует максимальная оценка, стано-
вится на текущей итерации базисной, а k-й столбец объявляется
ведущим столбцом.
5. Определение ведущей строки. Для этого находятся отношение правых частей ограничений к положительным элементам ведущего столбца и среди них выбирается минимальное:
 .
.
S-я строка объявляется ведущей строкой. Элемент, находящийся в симп-
лекс-таблице на пересечении s-й строки и k-го столбца ask, называется ведущим элементом.
6. Пересчет элементов симплекс-таблицы.При этом элементы ведущей строки as1,…, asn, bs делятся на ведущий элемент ask. Пересчет остальных элементов осуществляется по правилу прямоугольника.

| k-й столбец | j-й столбец | ||
| s-я строка | ask | аsj | ||
| i-я строка | aik | аij | ||
Пусть ask – ведущий элемент. Элемент aij– пересчитывается следующим образом:
 .
.
7. Переход к шагу 3
Оптимальное решение определяется следующим образом: базисные переменные приравниваются соответствующим правым частям, остальные нулю.
Пример
x1-x2-3x3®min
2x1-x2+x3 £ 1
4x1-2x2+x3 ³ -2
3x1+x3 £ 5
x1, x2, x3 ³ 0
Приведем к каноническому виду
x1-x2-3x3®min
2x1-x2+x3+x4 = 1
-4x1+2x2-x3+x5 = 2
3x1+ x3+x6 = 5
x1, x2, x3 ³ 0
Составим “симплекс-таблицу”:
| xб | Сб | b | -1 | -3 | ||||
| x1 | x2 | x3 | x4 | x5 | x6 | |||
| x4 | -1 | |||||||
| x5 | -4 | -1 | ||||||
| x6 | ||||||||
| -1 | ||||||||
| x3 | -3 | -1 | ||||||
| x5 | -2 | |||||||
| x6 | -1 | |||||||
| -3 | -7 | -3 | ||||||
| x3 | -3 | |||||||
| x2 | -1 | -2 | ||||||
| x6 | -2 | -1 | ||||||
| -15 | -7 | -4 | ||||||
| x3 | -3 | |||||||
| x2 | -1 | 11/3 | -1/3 | 1/3 | 2/3 | |||
| x1 | 1/3 | -2/3 | -1/3 | 1/3 | ||||
| -46/3 | -19/3 | -11/3 | -1/3 |
Оптимальное решение:
x1=1/3; x2=11/3; x3=4; x4=0; x5=0; x6=0.
Метод искусственного базиса
Как было указано выше, решение ЗЛП симплексным методом начинается с указания какого-либо первоначального опорного плана. Для ЗЛП, записанной в канонической форме, можно непосредственно указать опорный план, если среди векторов Aj, компонентами которых служат коэффициенты при переменных в системе ограничений данной задачи, есть m единичных (т.е., имеются m базисных переменных). Однако для многих ЗЛП, записанных в канонической форме, не всегда можно сразу определить опорный план. Рассмотрим задачу

Пусть в данной задаче среди векторов
 нет единичных.
нет единичных.
В данном случае к каждому i-му уравнению системы ограничений добавляется неотрицательная переменная xn+i, называемая искусственной переменной. Так как введение искусственных переменных, в отличие от дополнительных, меняет множество решений задачи, то они вводятся также и в выражение для целевой функции с очень большим коэффициентом M > 0 (тогда в процессе решения задачи минимизации искусственные переменные будут стремиться к нулю). В результате получается задача, называемая расширенной по отношению к исходной:
 ;
;
 ;
;
 .
.
В результате может быть указан первоначальный опорный план. Искусственные переменные приравниваются к правым частям (xn+i=bi), остальные – нулю ( ). Тогда целевая функция примет вид:
). Тогда целевая функция примет вид:
 ,
,
а оценки Dj в данном случае будут складываться из двух частей, одна из которых зависит от М, а другая не зависит:
 .
.
Исходные данные расширенной задачи заносят в симплекс-таблицу, которая содержит на строку больше, чем обычная. В последнюю, (m + 2)-ю строку оценок таблицы записывают коэффициенты при M, а в (m + 1)-ю - слагаемые, не содержащие M.
Так как знак Dj определяется знаком коэффициента, стоящего при M, ведущий столбец (и соответственно базисную переменную) выбирают по наибольшему положительному элементу (m + 2)-й строки таблицы. Пересчет симплекс-таблицы при переходе от одного опорного плана к другому производят по общим правилам симплексного метода. Итерационный процесс по (m + 2)-й строке ведут до тех пор, пока
1) либо все искусственные переменные не будут исключены из базиса;
2) либо не все искусственные переменные будут исключены, но (m + 2)-я
строка не содержит больше положительных элементов.
В первом случае полученное базисное решение соответствует некоторому опорному плану исходной задачи, (m+2)-я строка таблицы вычеркивается и решение задачи продолжают обычным симплексными методом. Во втором случае, если элемент, стоящий в (m + 2)-й строке столбца B положителен, задача не имеет решения, если он равен нулю, то базис содержит по крайней мере один из векторов искусственного базиса.
Если в процессе решения задачи какая-либо искусственная переменная выводится из базиса, то соответствующий столбец симплекс-таблицы можно вычеркнуть и не пересчитывать (т.к. эту переменную не имеет смысла вводить ни в один из последующих базисов).
Рассмотренный метод построения начального опорного плана называется методом искусственного базиса.
Таким образом алгоритм метода включает следующие шаги:
1. Составляется расширенная задача
2. Находится опорный план решения задачи
3. С использованием симплекс-метода искусственные переменные исключаются из базиса. В результате получается некоторый опорный план исходной задачи.
4). Нахождение оптимального плана исходной задачи с использованием симплекс-метода.
Пример:



| xб | Сб | b | -2 | -6 | -1 | M | |||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |||
| x4 | -1 | -2 | |||||||
| x5 | |||||||||
| x7 | M | -1 | -1 | ||||||
| -24 | -4 | ||||||||
| -1 | -1 | ||||||||
| x4 | -1 | -1 | |||||||
| x5 | -1 | ||||||||
| x3 | -6 | 1/2 | -1/2 | -1/2 | |||||
| -64 | -4 | ||||||||
| x4 | -1 | 5/2 | 1/2 | ||||||
| x6 | -1/2 | 1/2 | |||||||
| x3 | -6 | 11/2 | 1/4 | 1/2 | 1/4 | ||||
| -68 | -2 | -8 | -2 |
Ответ: x*=(0; 0; 11/2; 35; 0; 1).
Двойственность в линейном программировании
Каждой ЗЛП можно поставить в соответствие двойственную в соответствии с следующими правилами:
1) если целевая функция F исходной задачи стремится к минимуму, то целевая функция Ф двойственной задачи – к максимуму и наоборот;
2) число переменных двойственной задачи равно числу ограничений исходной, число ограничений двойственной задачи равно числу переменных исходной. Каждому i-му ограничению исходной задачи соответствует переменная yi двойственной задачи (двойственная переменная), а каждой j-й переменной исходной задачи соответствует j-е ограничение исходной задачи;
3) коэффициентами при переменных целевой функции двойственной задачи являются правые части ограничений исходной задачи, а правыми частями ограничений двойственной задачи являются коэффициенты при целевой функции в исходной задаче;

4) матрица коэффициентов при двойственных переменных в системе ограничений двойственной задачи является транспонированной матрицей коэффициентов при переменных в ограничениях исходной задачи;
5) для удобства построения двойственных задач рекомендуется в исходной задаче ограничения-неравенства записывать со знаком “£ ” при максимизации и со знаком “ ³” при минимизации;
6) каждому i-му ограничению – неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности (yi³0), а ограничению -равенству - переменная yi произвольного знака;
7) неотрицательной переменной исходной задачи xj³0 соответствует в двойственной задаче j-е ограничение – неравенство, а произвольной переменной xj - равенство. При этом если двойственная задача подлежит минимизации, неравенство записывается со знаком “ ³”, а если двойственная задача подлежит максимизации – со знаком “£ ”.
 |
Рассмотренные правила построения двойственных задач иллюстрируются табл. 8.
Таблица 8
Соотношение двойственности является взаимным, то есть задача двойственная по отношению к двойственной совпадает с исходной.
Пример 5. Построить двойственную задачу к задаче определения производственного плана, приведенной в примере 1: определить, сколько продукции каждого вида xj необходимо изготовить, чтобы при заданной прибыли от реализации единицы продукции cj и заданных размерах имеющихся ресурсов bi максимизировать общую прибыль.
Математическая модель задачи из примера 1 формулировалась следую-щим образом:
F=7x1+3x2+6x3+12x4®max;
3x1+x2+2x3+4x4 £440;
x1+8x2+6x3+2x4 £200;
x1+4x2+7x3+2x4 £320;
xj ³0, j=  .
.
Введя три двойственные переменные y1 , y2 , y3 , в соответствии с приве-денными выше правилами построим двойственную задачу:
Ф=440у1+200y2+320у3®min;
3y1+y2+y3 ³7;
y1+8y2+4y3 ³3;
2y1+6y2+7y3³6;
4y1+2y2+2y3 ³12;
yi ³0, j=  .
.
Отсюда видно, что двойственная задача заключается в определении стоимости единицы ресурса yi, чтобы при заданных количествах ресурсов bi и заданной прибыли cj от реализации единицы продукции минимизировать общую стоимость ресурсов.
Рассмотрим экономическую интерпретацию двойственных задач. Обратимся к задаче составления производственного плана.
Исходная задача: сколько и какой продукции хj (j=1, n) необходимо произвести, чтобы при заданной прибыли от выпуска единицы каждого вида продукции Cj и размерах имеющихся ресурсов bi максимизировать общую прибыль

C j -прибыль от единицы продукции j-го вида, х j - количество единиц продукции j-го вида, max - доход (прибыль)
 , где
, где
aij - затраты i-го ресурса на производство единицы продукции j-го вида, xj - количество единиц продукции j-го вида, bi - запас i-го ресурса,
 -общие затраты i-го ресурса на производство всей продукции.
-общие затраты i-го ресурса на производство всей продукции.
Не нашли, что искали? Воспользуйтесь поиском: