Дифференциальное уравнение движения невязкой жидкости

В движущейся жидкости выберем элементарный объем жидкости в виде параллелепипеда, грани которого параллельны координатным осям (x,z,y). На данный выделенный объем жидкости действуют массовые силы, пропорциональные массе, поверхностные силы давления окружающей жидкости, направленные по нормалям к граням параллелепипеда, а так же сила инерции вызывающая движение жидкости. Рассмотрим действие данных сил в проекции на ось х.

Рис 5.1. К выводу уравнения движущейся жидкости в форме Эйлера

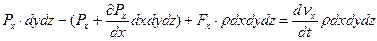
Проведем преобразования, получим

Поделим все на 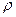и поменяем знаки

Система дифференциальных уравнений Л. Эйлера для идеальной движущейся жидкости на координатные оси

(5.1)

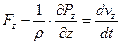
Если дифференциальная форма уравнений не может быть использована во всем пространстве, заполненном жидкой средой, то используется ее интегральная форма.

Для случая движения жидкости уравнение имеет вид:

(5.2)

где - главный вектор массовых сил; - главный вектор поверхностных сил; - изменение количества движения массы в объеме ; - вектор поверхностных сил на площадке по нормали .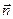

Предполагая, что масса выделенного объема постоянна, дифференцируя правую часть уравнения (5.2) по времени, получим интегральную форму уравнения движения:

(5.3)

Преобразуем поверхностный интеграл по формуле Остроградского-Гаусса в объемный

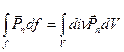(5.4)

Подставив (5.4) в (5.3) получим:

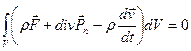
Так как объем остается произвольным, то ,тогда

(5.5)

Данное уравнение (5.5) представляет собой векторную форму уравнения движения сплошной среды, и называется дифференциальным уравнением движения в напряжениях.

Для идеальной жидкости при отсутствии поверхностных касательных сил , дифференциальное уравнение (5.5) упрощается и записывается:

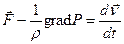(5.6)

При движении идеальной жидкости или газа, нормальное напряжение в произвольной точке потока не зависит от направления площадки, к которой оно приложено. Дифференциальное уравнение (5.6) записывается как уравнение (5.1).

Уравнение Бернулли

Профессор Казанского университета И.С. Громека преобразовал уравнения Эйлера в иную форму, соответствующую идеальной, несжимаемой, однородной жидкости. Массовые силы для большинства практических задач соответствовали силе тяжести. Режим движения данной жидкости был стационарным, т.е. 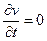и безвихревой.

Умножим каждое из уравнений Эйлера последовательно на , , и .

Система дифференциальных уравнений Л. Эйлера для идеальной движущейся жидкости на координатные оси

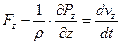
Раскроем скобки и сгруппируем, получим:

(5.7)

Это выражение называют уравнением Бернулли в дифференциальной форме. При условии (для несжимаемой жидкости) интегрирование его дает:

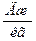, (5.8)

Этот интеграл называют интегралом Бернулли, из уравнения (5.8.) следует, что сумма удельной кинетической , удельной потенциальной энергии и удельной работы сил давления - есть величина постоянная.

Для того, чтобы записать интеграл Бернулли в размерностях давления, умножим обе части (5.8) на плотность 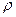и получим

(5.9)

(5.10)

где:

- удельная потенциальная энергия единицы объема жидкости, Па.

геометрическое давление - удельная энергия положения единицы объема жидкости, Па.

скоростное давление - удельная кинематическая энергия единицы объема жидкости, Па.

Таким образом, уравнение Бернулли это частный случай закона сохранения энергии.

Не нашли, что искали? Воспользуйтесь поиском: