Распределение Максвелла

dN = Ndw = Nf( υ )d υ. (18.3)

Наряду с распределением молекул по величине скорости υ, можно ввести также функцию распределения молекул 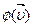по направлению вектора скорости или, что тоже самое, по значениям проекции вектора скорости на оси φ ( υ _x, υ _y, υ _z) Распределение φ ( υ _x, υ _y, υ _z) позволяет определить число моле­кул dN_Xy_Z, у которых проекции скорости соответствуют ин­тервалам от υ _x до υ _x + d υ _x, от υ _y до υ _y + d υ _y,от υ _z до υ _z + d υ _z:

dN_XYZ = Nφ( υ _x, υ _y, υ _z)d υ _xd υ _yd υ _z. (18.4)

Так как движение молекул хаотично и на газ не действу­ют внешние силовые поля, то все направления движения молекул разновероятны, и функция распределения 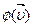не мо­жет зависеть от направления скорости . Это означает, что φ ( υ _x, υ _y, υ _z) зависит только от абсолютной величины скорости υ, т. е. φ ( υ _x, υ _y, υ _z) = φ ( υ ). Учитывая это обстоятельство, най­дем связь между функциями f( υ ) и φ ( υ ). Очевидно, что число dN молекул со скоростями в интервале от υдо υ + d υ (18.3) можно найти также путем сложения dN_xyz всех молекул с про­екциями скоростей в интервалах от υ _x до υ _x + d υ _x, от υ _y до υ _y + d υ _y, от υ _z до υ _z + d υ _z. Тогда, с учетом (18.4) получим:

(18.5)

Далее, так как φ ( υ _x, υ _y, υ _z) = φ ( υ ) является функцией аб­солютной величины скорости υ, то выражение (18.5) пред­ставится в виде

(18.6)

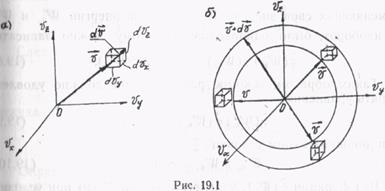
Для нахождения суммы, стоящей в качестве множителя в правой части формулы (18.6), воспользуемся графическим методом. С этой целью рассмотрим векторное пространство скоростей молекул (рис. 19.1). В этом пространстве с тремя взаимно перпендикулярными осями υ _x, υ _y,υ _z заданные интервалы проекций скорости на эти оси, т. е. интервалы от υ _x до υ _x + d υ _x, от υ _y до υ _y + d υ _y, от υ _z до υ _z + d υ _z, изобража­ются в форме кубика со сторонами d υ _x, υ _y, υ _z (рис. 19.1, а), объем которого равен произведению d υ _x υ _y υ _z. Сумма же

этихобъемов, стоящая в (18.6), в векторном пространстве скоростей представляется объемом шарового слоя, радиусом υ и толщиной d υ(рис. 19.1, б), который равен

.

Таким образом, формула (18.6) представится в виде

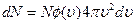. (18.7)

Сравнивая (18.3) и (18.7), получим

. (18.7′)

Перейдем теперь к установлению явного вида функции φ ( υ ).

Как уже отмечалось выше, распределение φ ( υ ) должно быть изотропно, т. е. функция φ ( υ ) зависит только от абсолютной величины скорости молекул газа.

Функция φ является также однозначной функцией кинетической энергии молекулы. Так как кинетическая энергия

, то

и .

Рассмотрим столкновение двух молекул с энергиями W_к1 и W_к2. В идеальном газе столкновения абсолютно упругие, следовательно, в соответствии с законом сохранения энергии

W_к1 + W_к2 = W′_к1+ W′_к2,

где W′_к1 и W′_к2 — энергии молекул после столкновения. Число столкновений, в результате которых молекулы вместо энергий W_к1 и W_к2 приобретают энергии W′_к1 и W′_к2,пропорциональ­но произведению . Для того чтобы распределе­ние было стационарным, необходимо, чтобы число молекул, изменяющих свои энергии W_к1 и W_к2 на энергии W′_к1 и W′_к2 и наоборот, было одинаковыми. Поэтому можно записать:

. (18.8)

Таким образом, искомое распределение должно удовлет­ворять уравнению

; (18.9)

при дополнительном условии

W_кl + W_к2 = const. (18.10)

Вид функции ,удовлетворяющей (18.9) при условии (18.10), легко найти

(18.11)

где а и θ — константы, не зависящие от υ.

Действительно, при умножении двух функций вида (18.11) показатели экспонент складываются и произведение функций , будет постоянно, если постоянная сумма энергий W_к1 + W_к2.

Таким образом, функции распределения по скоростям φ ( υ ) и f( υ ) имеют вид

; (18.12)

. (18.13)

Для определения константы а воспользуемся свойством нормированной вероятности. Очевидно, что для молекулы ве­роятность иметь произвольную скорость есть вероятность до­стоверного события и поэтому она должна быть равна еди­нице. Эту вероятность получим, проинтегрировав плотность f( υ ) вероятности по всему интервалу изменения скорости, т. е.

(18.14)

Подставляя в (18.14) функцию (18.12), получим

Из таблицы интегралов следует, что

.

Следовательно,

откуда

. (18.15)

Определим теперь вторую постоянную θ. Для этого воспользуемся формулой (15.7) для средней кинетической энергии поступательного движения молекулы газа

,

из которой вытекает, что среднее значение квадрата скорости молекулы равно:

. (18.16)

Сдругой стороны, согласно теории вероятностей величину υ² можно вычислить, проинтегрировав произведение υ² f (υ) по всему интервалу изменения скорости:

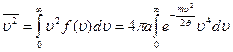. (18.17)

Из таблицы интегралов следует, что

. (18.18)

Следовательно, учитывая (18.16), (18.15), (18.17) и (18.18), имеем:

или . (18.19)

Итак, Максвелловское распределение молекул по скоростям (18.13) примет вид

. (18.20)

Распределение молекул по проекции скоростей (18.12) запишется в виде

. (18.21)

На рис. 19.2 представлены графики функции f(υ) при трех различных температурах. Исходя из геометрического толко­вания определенного интеграла и учитывая вероятностный смысл функции f(υ), приходим к выводу, что площадь, огра­ниченная любой из этих кривых и осью абцисс, постоянна и равна единице. Каждая кривая имеет максимум. С увеличе­нием температуры газа максимум смещается в сторону боль­ших скоростей, но его абсолютная величина уменьшается, так что площадь под кривой оказывается неизменной. Сама кри­вая при увеличении температуры становится более размытой, следовательно, при нагревании газа число молекул с более высокими скоростями увеличивается, а молекул с малыми скоростями уменьшается.

Скорость υ _b, соответствующая максимуму функции f(υ), называется наиболее вероятной скоростью. Для каждой тем­пературы газа Т ₁, Т ₂, Т ₃ имеется своя наиболее вероятная скорость υ _b1, υ _b2, υ _b3 (рис. 19.2). Смысл υ _b очевиден — это скорость, которой при данной температуре газа обладает наи­большее число молекул. С ростом температуры υ _b увели­чивается.

Наиболее вероятную скорость можно определить, исследовав функцию f( υ ) на экстремум. Для этого нужно, продиффе­ренцировав f( υ ) по переменной, приравнять производную нулю, при υ = υ _b:

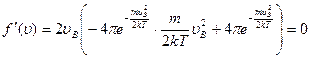
или

. (18.22)

Выбирая корень этого уравнения, не равный нулю, имеем

. (18.23)

Закон распределения молекул по скоростям (18.20) позво­ляет вычислить среднее значение любой величины F(υ), зави­сящей от скорости молекул. Согласно теории вероятности, среднее значение или математическое ожидание функции F(υ) равно

. (18.24)

Отметим, что мы уже воспользовались этой формулой при определении константы θ. Найдем теперь, используя свойство распределения (18.20), значение абсолютной величины сред­ней скорости

(18.25)

Из таблицы интегралов вытекает, что

.

Следовательно, средняя скорость равна

. (18.26)

Важное значение в теории имеет также средняя квадра­тичная скорость . Учитывая (18.16), имеем

. (18.27)

Таким образом, три характерных скорости 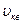, и от­личаются друг от друга множителями порядка единицы, при­чем, как видно из (18.23), (18.26) и (18.27),

> >

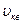Не нашли, что искали? Воспользуйтесь поиском: