
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
ЛЕКЦИЯ 4
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
Рассмотрим функцию  Точку
Точку  называют точкой (локального) минимума функции
называют точкой (локального) минимума функции  , если в некоторой окрестности
, если в некоторой окрестности  этой точки выполняется неравенство:
этой точки выполняется неравенство: 
Точку  называют точкой (локального) максимума функции
называют точкой (локального) максимума функции  , если в некоторой окрестности
, если в некоторой окрестности  этой точки выполняется неравенство:
этой точки выполняется неравенство:

Точки максимумов и минимумов называют точками экстремума функции, а значения функций в этих точках экстремальными или экстремумами.
Чтобы выделить из области определения заданной функции возможные точки экстремума, используют необходимые условия экстремума.
Теорема 1. (необходимые условия экстремума). Если точка  является точкой локального экстремума функции
является точкой локального экстремума функции  , то частные производные 1 -го порядка обращаются в нуль или конечные частные производные не существуют:
, то частные производные 1 -го порядка обращаются в нуль или конечные частные производные не существуют:
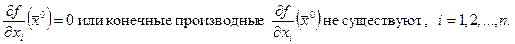 (1)
(1)
З а м е ч а н и е.Точки, удовлетворяющие условиям (5.27), называют критическими точками функции. Точки, в которых все частные производные одновременно обращаются в нуль, называют стационарными точками.
Последующий выбор точек экстремума из множества стационарных точек осуществляется при помощи достаточных условий экстремума.
Теорема 2. (достаточные условия экстремума). Пусть функция  определена и непрерывна вместе со своими частными производными до второго порядка включительно в некоторой окрестности стационарной точки
определена и непрерывна вместе со своими частными производными до второго порядка включительно в некоторой окрестности стационарной точки  и
и  .
.
Если второй дифференциал в этой точке положителен при любых значениях  то
то  − точка минимума:
− точка минимума: 
Если второй дифференциал в этой точке отрицателен при любых значениях  , то
, то  − точка максимума:
− точка максимума: 
Если второй дифференциал является знакопеременной величиной в точке  , то в этой точке нет экстремума.
, то в этой точке нет экстремума.
Если второй дифференциал неположителен или неотрицателен в точке  , то в этой точке требуется дополнительное исследование.
, то в этой точке требуется дополнительное исследование.
На практике удобнее выполнять исследование функции в стационарных точках с помощью другой теоремы − теоремы, базирующейся на теории квадратичных форм и критерии знакоопределенности квадратичной формы [У-к по лин.ал. ].
Матрицей Гессе 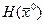 функции
функции  называют матрицу, составленную из частных производных второго порядка заданной функции
называют матрицу, составленную из частных производных второго порядка заданной функции
 где
где
 (2)
(2)
Заметим, что в сформулированных условиях 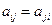 и матрица Гессе всегда симметрическая.
и матрица Гессе всегда симметрическая.
Угловые миноры этой матрицы равны следующим определителям:
 …,
…, 
Теорема 3. (достаточные условия экстремума с использованием критерия Сильвестра). Пусть функция  определена и непрерывна вместе со своими частными производными до второго порядка включительно в некоторой окрестности стационарной точки
определена и непрерывна вместе со своими частными производными до второго порядка включительно в некоторой окрестности стационарной точки  .
.
Если все угловые миноры матрицы Гессе положительны в стационарной точке  , то
, то  − точка минимума функции:
− точка минимума функции: 

Если угловые миноры матрицы Гессе в стационарной точке  образуют знакочередующуюся последовательность, первый элемент которой отрицателен, то
образуют знакочередующуюся последовательность, первый элемент которой отрицателен, то  − точка максимума функции:
− точка максимума функции: 

Если все миноры отличны от нуля и не подчиняются сформулированным правилам чередования знаков, то в точке  нет экстремума.
нет экстремума.
Рассмотрим два частных случая.
1. Для функции двух переменных  стационарная точка
стационарная точка  является решением системы уравнений:
является решением системы уравнений:
 (3)
(3)
С учетом (2) имеем:

Если функция  удовлетворяет условиям теоремы 1 и
удовлетворяет условиям теоремы 1 и  в стационарной точке
в стационарной точке  , то
, то  − точка экстремума, причем при
− точка экстремума, причем при 
 − точка минимума; при
− точка минимума; при 
 − точка максимума. Если
− точка максимума. Если 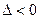 в стационарной точке
в стационарной точке  , то в этой точке нет экстремума. Если
, то в этой точке нет экстремума. Если  в стационарной точке
в стационарной точке  , то для решения вопроса нужно привлекать производные более высоких порядков.
, то для решения вопроса нужно привлекать производные более высоких порядков.
2. Для функции трех переменных  стационарная точка
стационарная точка  является решением системы уравнений:
является решением системы уравнений:
 (4)
(4)
С учетом (2) имеем:
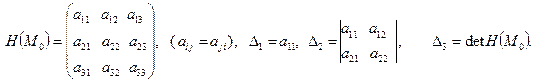
Пусть функция  удовлетворяет условиям теоремы. Если
удовлетворяет условиям теоремы. Если  в стационарной точке
в стационарной точке  , то
, то  − точка минимума.
− точка минимума.
Если 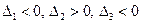 в стационарной точке
в стационарной точке  , то
, то  − точка максимума.
− точка максимума.
Если все миноры отличны от нуля и не подчиняются сформулированным правилам чередования знаков, то в точке  нет экстремума.
нет экстремума.
При исследовании функции нескольких переменных можно использовать:
АЛГОРИТМ 1 исследования функции нескольких переменных на экстремум
1) Найти стационарные точки  функции
функции  из необходимых условий экстремума:
из необходимых условий экстремума:  .
.
2) В каждой найденной стационарной точке 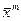 применить достаточные условия экстремума теоремы 3 для отбора точек экстремума.
применить достаточные условия экстремума теоремы 3 для отбора точек экстремума.
3) Вычислить экстремальные значения функции.
Пример 1. Исследовать на экстремум функцию 
□ 1-й шаг. Используем необходимые условия экстремума дифференцируемой функции трех переменных: 
Найдем частные производные: 

Упростим полученные выражения:

Составим и решим систему алгебраических уравнений:

Система имеет единственное решение  Стационарная точка
Стационарная точка  − единственная точка возможного экстремума.
− единственная точка возможного экстремума.
2-й шаг. Используем достаточные условия экстремума дифференцируемой функции двух переменных с использованием критерия Сильвестра.
Найдем все частные производные второго порядка заданной функции:
 ,
,
Составим матрицу Гессе: 
 Эта числовая матрица соответствует данной квадратичной функции (форме).
Эта числовая матрица соответствует данной квадратичной функции (форме).
Вычислим угловые миноры:

Так как 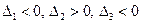 в стационарной точке
в стационарной точке  , то
, то  − точка максимума.
− точка максимума.
Таким образом, единственная точка экстремума − это точка максимума  .
.
3-й шаг. Вычислим экстремальное значение функции:
 ■
■
Пример 2. Исследовать на экстремум функцию  .
.
□ 1-й шаг. Используем необходимые условия экстремума дифференцируемой функции двух переменных: 
Найдем частные производные 
Составим и решим систему алгебраических уравнений:

Система имеет два решения:  и
и  . Эти пары чисел являются координатами стационарных точек
. Эти пары чисел являются координатами стационарных точек  и
и  − точек, «подозрительных» на экстремум.
− точек, «подозрительных» на экстремум.
2-й шаг. Используем достаточные условия экстремума дифференцируемой функции двух переменных с использованием критерия Сильвестра.
Найдем все частные производные второго порядка заданной функции:
 ,
,
Составим матрицу Гессе:  .
.
В каждой стационарной точке вычислим элементы матрицы и ее определитель.
Начинаем вычисления с точки  :
:

Так как  , то
, то  является точкой экстремума. При этом
является точкой экстремума. При этом  − точка минимума, так как
− точка минимума, так как  Значение функции в этой точке равно
Значение функции в этой точке равно  .
.
Продолжим вычисления в точке  :
:

Так как 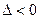 , то
, то  не является точкой экстремума. Таким образом, единственная точка экстремума − это точка минимума
не является точкой экстремума. Таким образом, единственная точка экстремума − это точка минимума  .
.
3-й шаг. Вычислим экстремальное значение функции:
 .■
.■
| <== предыдущая лекция | | | следующая лекция ==> |
| Унификация и агрегатирование изделий | | | Лекция 4. Информационная безопасность |
Не нашли, что искали? Воспользуйтесь поиском: