ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ЛЕКЦИЯ 7
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
N-ГО ПОРЯДКА
Уравнение
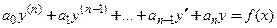(1)
называется линейным неоднородным дифференциальным уравнением n-го порядка, если коэффициенты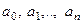 
являются действительными числами или функциями переменной 
: 
функция 
.
Если функция 
то уравнение (1) принимает вид:
. (2)
Уравнение (2) называют линейным однородным дифференциальным уравнением n-го порядка, соответствующим (отвечающим) неоднородному уравнению (1).
Свойства решений линейных однородных уравнений
1. Если 
решение линейного однородного уравнения (2) на интервале 
, то для любого числа 
функция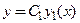 
также является решением этого уравнения (2) на .
2. Если 
решения уравнения (2) на интервале , то 
также является решением уравнения (2 ) на .
С л е д с т в и е. Если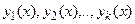 
являются решениями уравнения (2) на интервале , то 
также является решением этого уравнения на при любых значениях произвольных постоянных 
.
В теории линейных дифференциальных уравнений важную роль играет понятие линейной независимости системы функций на интервале.
Функции 
называются линейно независимыми на интервале , если для любого 
линейная комбинация функций обращается в нуль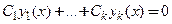 
тогда и только тогда, когда 
.
В противном случае эти функции называются линейно зависимым на .
Проверку линейной независимости системы решений однородного уравнения n-го порядка удобно выполнять при помощи следующей теоремы.
Теорема 1. Чтобы решения линейного однородного уравнения n-го порядка 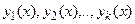были линейно независимы на , необходимо и достаточно, чтобы определитель Вронского 
был отличен от нуля для 
:
. (3)
Фундаментальной системой решений линейного однородного уравнения n-го порядка на интервале называют набор n решений 
этого уравнения, линейно независимых на .
В теореме 1 сформулирован критерий фундаментальности набора (системы) n решений линейного однородного уравнения n-го порядка.
Теорема 2 (об общем решении линейного однородного уравнения). Если функции образуют фундаментальную систему решений линейного однородного уравнения n-го порядка (2) на интервале , то общее решение 
этого уравнения имеет вид:
, (4)
где 
произвольные постоянные.
Теорема 3 (об общем решении линейного неоднородного уравнения). Если функция является общим решением однородного уравнения (2), 
является частным решением неоднородного уравнения (1), то функция
(5)
является общим решением уравнения (1).
З а м е ч а н и е (п р и н ц и п с у п е р п о з и ц и и). Если правая часть линейного неоднородного уравнения является суммой функций: 
то частное решение 
где 
частные решения неоднородных уравнений (2) с правыми частями, равными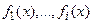 
соответственно.
Пример 1. Проверить фундаментальность системы решений 
дифференциального уравнения 
и записать его общее решение.
□ Непосредственной подстановкой функций 
в уравнение убеждаемся в том, что они действительно являются его решениями:
Проверим, являются ли решения уравнения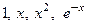 
линейно независимыми. Для этого воспользуемся теоремой 1. Составим определитель Вронского:
Известно, что определитель треугольной матрицы равен произведению диагональных элементов: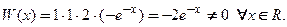 
Значит, определитель Вронского отличен от нуля на всей числовой оси. Из теоремы 1 следует, что данная система функций фундаментальная. По теореме 2 составляем общее решение линейного однородного дифференциального уравнения:
■
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим линейное дифференциальное уравнение n-го порядка
(6)
где коэффициенты 
Такое уравнение называют линейным однородным дифференциальным уравнением с постоянными коэффициентами.
При помощи подстановки Эйлера 
процедура решения линейного уравнения (6) сводится к отысканию корней алгебраического уравнения:
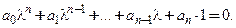(7)
Это уравнение (7) и многочлен, корни которого следует найти, называют характеристическим уравнением и характеристическим многочленом соответственно.
Корни характеристического многочлена с действительными коэффициентами могут быть как действительными, так и комплексными числами (см. разд. 1.2.3 и 1.6.5).
Рассмотрим два случая.
1. Пусть 
действительный корень уравнения (7) кратности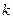 
. Можно доказать, что этому корню соответствует ровно 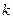линейно независимых решений:
(8)
При 
корень 
называется простым. Простому действительному корню соответствует единственное решение 
.
2. Пусть 
комплексный корень кратности 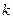. Тогда комплексное число 
также является корнем кратности 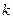характеристического многочлена с действительными коэффициентами. Этой паре комплексно-сопряженных чисел соответствует 2 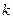частных линейно независимых решений уравнения (6):
(9)
Частные решения, соответствующие разным корням характеристического уравнения (7), линейно независимы.
Как только найдено n частных линейно независимых решений, по теореме 2 можно написать общее решение в виде их линейной комбинации.
Алгоритм 1 решения линейного однородного уравнения с постоянными коэффициентами
1. Составить характеристическое уравнение (7).
2. Найти все корни уравнения (7) и определить их кратности.
3. Для каждого найденного корня написать соответствующие частные решения по
формулам (8) или (9).
4. Составить фундаментальную систему решений и записать общее решение по формуле (4).
Не нашли, что искали? Воспользуйтесь поиском: