
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ЛЕКЦИЯ 8
ЛИНЕЙНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В НОРМАЛЬНОМ ВИДЕ
Рассмотрим систему уравнений вида:
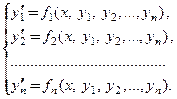 (1)
(1)
Система (1) является системой дифференциальных уравнений относительно неизвестных функций 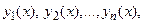 которые входят в уравнения системы под знаками производных. Набор функций
которые входят в уравнения системы под знаками производных. Набор функций 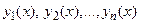 называется решением системы на некотором интервале
называется решением системы на некотором интервале 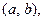 если при подстановке этих функций в уравнения системы каждое уравнение обращается в верное равенство для любого
если при подстановке этих функций в уравнения системы каждое уравнение обращается в верное равенство для любого 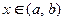 .
.
Систему (1) называют системой дифференциальных уравнений, приведенной к нормальному виду. Каждое уравнение этой системы имеет первый порядок, всю систему называют системой 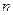 -го порядка по числу уравнений.
-го порядка по числу уравнений.
В левых частях уравнений системы (1) производные часто записывают в виде 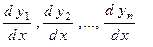 вместо
вместо 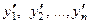 . Если независимая переменная носит имя
. Если независимая переменная носит имя 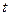 (время), то производные искомых функций обозначают
(время), то производные искомых функций обозначают 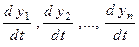 , или
, или 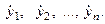
Всякую систему дифференциальных уравнений 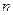 -го порядка можно записать в векторно-матричной форме. Введем следующие матрицы:
-го порядка можно записать в векторно-матричной форме. Введем следующие матрицы:
матрицу-столбец (вектор-функцию) решений 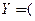
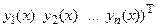 ,
,
матрицу-столбец правых частей системы 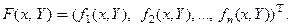
Производной 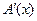 матрицы
матрицы 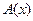 называют матрицу, элементы которой равны производным элементов исходной матрицы. Отметим, что правила дифференцирования матриц повторяют правила дифференцирования функций одной переменной.
называют матрицу, элементы которой равны производным элементов исходной матрицы. Отметим, что правила дифференцирования матриц повторяют правила дифференцирования функций одной переменной.
Согласно введенному определению
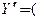
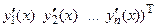 .
.
Тогда систему (1) можно записать в матричном виде:
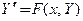 . (2)
. (2)
Приведенная форма записи системы компактна и по этой причине далее часто используется. Запись (1) называют скалярной формой записи системы дифференциальных уравнений, а (2) − матричной формой, или векторно-матричной формой.
Пример 1. Записать в векторно-матричной форме систему дифференциальных уравнений 2-го порядка
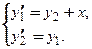
□ Введем следующие матрицы: 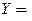
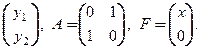 Тогда
Тогда
векторно-матричная форма записи заданной системы такова:
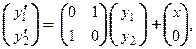 или
или 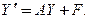 ■
■
Задача Коши для системы дифференциальных уравненийсостоит в отыскании такого решения системы (1), которое удовлетворяет начальным условиям:
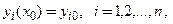 или
или 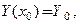 (3)
(3)
где 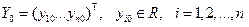 .
.
Теорема 1 (существования и единственности решения). Если элементы матрицы 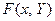 непрерывны и имеют ограниченные частные производные
непрерывны и имеют ограниченные частные производные 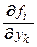 для любых
для любых  в некоторой области
в некоторой области 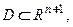 то при любых начальных условиях
то при любых начальных условиях 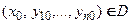 существует и притом единственное решение
существует и притом единственное решение 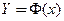 (
(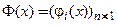 ) задачи Коши (2),(3), определенное в некоторой окрестности точки
) задачи Коши (2),(3), определенное в некоторой окрестности точки 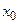 и удовлетворяющее как системе уравнений:
и удовлетворяющее как системе уравнений: 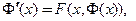 так и начальным условиям
так и начальным условиям 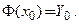
Вектор-функцию 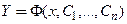 называют общим решением системы (2) в области
называют общим решением системы (2) в области 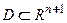 , если:
, если:
1) при любых значениях произвольных постоянных она является решением системы; 2) для любых начальных условий 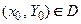 существует набор значений произвольных постоянных
существует набор значений произвольных постоянных 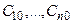 , при которых
, при которых 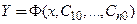 удовлетворяет заданным начальным условиям (3), т.е. является решением задачи Коши.
удовлетворяет заданным начальным условиям (3), т.е. является решением задачи Коши.
Между системами дифференциальных уравнений 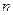 -го порядка и дифференциальными уравнениями
-го порядка и дифференциальными уравнениями 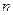 -го порядка существует связь. Всякое дифференциальное уравнение п-го порядка может быть сведено к решению системы дифференциальных уравнений п-го порядка, и всякая система п-го порядка, записанная в нормальном виде, может быть сведена к решению дифференциального уравнения, порядок которого не превышает числа п. Проиллюстрируем приведенное утверждение на двух примерах.
-го порядка существует связь. Всякое дифференциальное уравнение п-го порядка может быть сведено к решению системы дифференциальных уравнений п-го порядка, и всякая система п-го порядка, записанная в нормальном виде, может быть сведена к решению дифференциального уравнения, порядок которого не превышает числа п. Проиллюстрируем приведенное утверждение на двух примерах.
Пример 2. Решить систему дифференциальных уравнений 2-го порядка
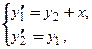 (4)
(4)
сведя ее к дифференциальному уравнению.
□ Исключим из системы (4) функцию 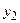 и ее производную. Для этого используем первое уравнение системы (3), откуда
и ее производную. Для этого используем первое уравнение системы (3), откуда
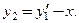 (5)
(5)
Подставим 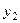 во второе уравнение системы:
во второе уравнение системы: 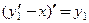 и получим
и получим
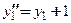 . (6)
. (6)
Это уравнение является дифференциальным уравнением 2-го порядка относительно функции 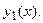 Если функция
Если функция 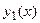 − решение этого уравнения, то вторая функция
− решение этого уравнения, то вторая функция 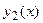 может быть найдена из уравнения (5).
может быть найдена из уравнения (5).
Перепишем уравнение (6): 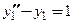 . Это уравнение является линейным неоднородным уравнением 2-го порядка со специальной правой частью. Его общее решение имеет вид:
. Это уравнение является линейным неоднородным уравнением 2-го порядка со специальной правой частью. Его общее решение имеет вид: 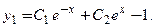 Подставим
Подставим 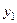 в формулу (5) и найдем
в формулу (5) и найдем 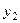 :
:
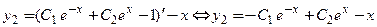 .
.
Общее решение системы (4) имеет вид: 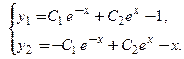
В векторно-матричной форме ответ можно записать так:
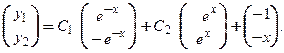 ■
■
В приведенных примерах показано, как выполнять переходы от системы дифференциальных уравнений к дифференциальному уравнению относительно одной из функций в системе, и, наоборот, от уравнения к системе.
Заметим, что в ранее приведены приемы решения дифференциальных уравнений высших порядков, фактически состоящие в переходах от дифференциальных уравнений высших порядков к системам дифференциальных уравнений меньших порядков.
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Систему
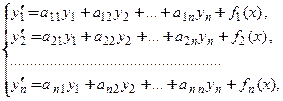 (7)
(7)
называют линейной системой дифференциальных уравнений относительно неизвестных функций 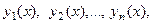 , если коэффициенты
, если коэффициенты 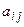 − действительные числа или функции переменной
− действительные числа или функции переменной 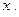 Запишем эту систему в векторно-матричной форме:
Запишем эту систему в векторно-матричной форме:
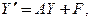 (8)
(8)
где 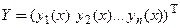 , − матрица-столбец, или вектор-функция решений,
, − матрица-столбец, или вектор-функция решений, 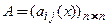 − матрица коэффициентов,
− матрица коэффициентов, 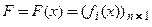 − матрица-столбец правых частей уравнений системы.
− матрица-столбец правых частей уравнений системы.
Если 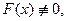 то систему (8) называют системой линейных неоднородных дифференциальных уравнений.
то систему (8) называют системой линейных неоднородных дифференциальных уравнений.
Если 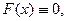 то систему
то систему
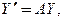 (9)
(9)
называют системой линейных однородных дифференциальных уравнений. Говорят, что система (9) является однородной системой, соответствующей данной неоднородной системе. Обе системы − однородная и неоднородная − имеют п -й порядок. В теории систем дифференциальных уравнений используют сокращения (аббревиатуры) ЛОСУ и ЛНСУ для линейных однородных и линейных неоднородных систем уравнений соответственно.
Системы (7)−(9) называют системами с переменными коэффициентами, если хотя бы один элемент матрицы 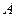 зависит от
зависит от 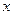 , в противном случае говорят о системах с постоянными коэффициентами.
, в противном случае говорят о системах с постоянными коэффициентами.
Свойства решений ЛОСУ 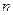 -го порядка
-го порядка
1. Если 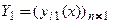 − решение однородной системы (9), то для любого числа
− решение однородной системы (9), то для любого числа 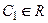 вектор-функция
вектор-функция 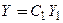 также является решением этой системы.
также является решением этой системы.
2. Если вектор-функции 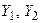 − решения системы (9), то
− решения системы (9), то 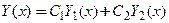 также является решением этой системы при любых значениях постянных
также является решением этой системы при любых значениях постянных 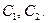
С л е д с т в и е. Если вектор-функции 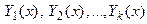 являются решениями однородной системы (9), то
являются решениями однородной системы (9), то 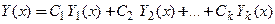 также является решением этой системы при любых значениях произвольных постоянных
также является решением этой системы при любых значениях произвольных постоянных 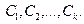
Вектор-функции 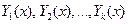 называются линейно независимыми на интервале
называются линейно независимыми на интервале 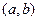 , если для любого
, если для любого 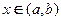 линейная комбинация функций обращается в нуль
линейная комбинация функций обращается в нуль 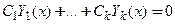 (
(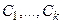 − произвольные постоянные) тогда и только тогда, когда
− произвольные постоянные) тогда и только тогда, когда 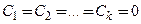 .
.
В противном случае эти функции называются линейно зависимыми на интервале 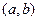 .
.
Пусть система вектор-функций 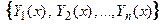 образована
образована 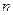 решениями однородной системы (9) Эту систему называют фундаментальной системой решений (ФСР) ЛОСУ
решениями однородной системы (9) Эту систему называют фундаментальной системой решений (ФСР) ЛОСУ 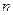 - го порядка, если решения
- го порядка, если решения 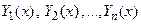 линейно независимы на интервале
линейно независимы на интервале 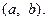
Из определения ФСР следует, что набор вектор-функций 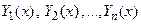 , образующих ФСР ЛОСУ, характеризуется тремя признаками: 1) каждая вектор-функция является решением ЛОСУ, 2) вектор-функции линейно независимы между собой на
, образующих ФСР ЛОСУ, характеризуется тремя признаками: 1) каждая вектор-функция является решением ЛОСУ, 2) вектор-функции линейно независимы между собой на  3) число п вектор-функций в ФСР равно порядку ЛОСУ.
3) число п вектор-функций в ФСР равно порядку ЛОСУ.
Проверку линейной независимости системы решений линейной однородной системы n-го порядка удобно выполнять при помощи следующей теоремы.
Теорема 8.7 (критерий фундаментальности системы решений). Чтобы 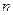 решений
решений 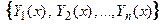 линейной однородной системы
линейной однородной системы 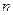 -го порядка образовывали фундаментальную систему решений (ФСР) на интервале
-го порядка образовывали фундаментальную систему решений (ФСР) на интервале 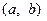 , необходимо и достаточно, чтобы определитель Вронского (вронскиан)
, необходимо и достаточно, чтобы определитель Вронского (вронскиан) 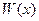 был отличен от нуля в каждой точке этого интервала:
был отличен от нуля в каждой точке этого интервала:
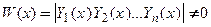 ,
,
или 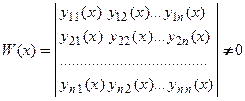 . (10)
. (10)
Теорема 2 (об общем решении линейной однородной системы 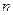 -го порядка). Если
-го порядка). Если 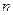 решений
решений 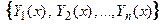 образуют фундаментальную систему решений линейной однородной системы
образуют фундаментальную систему решений линейной однородной системы 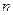 -го порядка
-го порядка 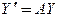 на интервале
на интервале 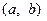 , то общее решение этой системы является линейной комбинацией решений фундаментальной системы:
, то общее решение этой системы является линейной комбинацией решений фундаментальной системы:
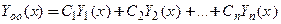 . (11)
. (11)
Не нашли, что искали? Воспользуйтесь поиском: