МЕТОД ПОДБОРА ДЛЯ РЕШЕНИЯ ЛНСУ

Интегрирование линейной неоднородной системы дифференциальных уравнений по аналогии с соответствующими процедурами для неоднородных уравнений п- го порядка можно выполнять разными методами, из которых выберем метод подбора частного решения и метод вариации произвольных постоянных (метод Лагранжа). Ниже приведены описания этих методов, которые сопровождены примерами.

Метод подбора частного решения для линейной неоднородной системы

Рассмотрим линейную неоднородную систему n -го порядка с постоянными действительными коэффициентами , записанную в векторно-матричной форме:

. (2)

Если правая часть системы имеет вид

(3)

где − вектор-функции, компонентами которых являются многочлены, степени которых не превосходят чисел и , то систему (3) называют системой неоднородных уравнений со специальной правой частью. Можно доказать, что частное решение 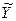этой системы представимо в виде

, (4)

где − вектор-функции, компонентами которых являются многочлены степеней 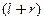с неопределенными коэффициентами,

,

Алгоритм 4 решения неоднородной системы со специальной правой частью

1. Найти общее решение соответствующей однородной системы согласно алгоритму 3.

2.Методом подбора найти частное решение 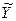заданной неоднородной системы.

3. Составить общее решение неоднородной системы по формуле .

Пример 1. Решить систему дифференциальных уравнений

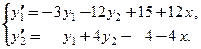
□ Данная система является линейной неоднородной системой дифференциальных уравнений 2-го порядка с постоянными коэффициентами и специальной правой частью. Используем алгоритм 4.

1. Интегрируем соответствующую однородную систему

(см. алгоритм 3).

1. Система для матрицы имеет вид:

(5)

Характеристическое уравнение:

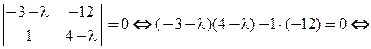
2. Решим неполное квадратное уравнение: Разложим на множители и получим: Кратности корней, называемых собственными числами матиры А, равны единице (1-й случай корней характеристического уравнения).

3. По очереди подставляем найденные собственные числа 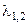матрицы A в систему (5) и находим собственные векторы.

При система (5) имеет вид

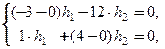или

Если принять то из уравнений следует, что Собственный вектор . Тогда частное решение имеет вид: или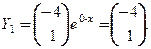

Второму числу соответствует система

или

По аналогии с первым случаем полагаем и получаем Значит, собственный вектор матрицы А, соответствующий собственному числу 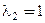, равен . Второе частное решение: или

4. Фундаментальная система решений состоит из двух вектор-функций , полученных выше. Общее решение составим по формуле (8.36):

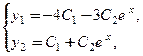, или (6)

где 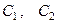− произвольные постоянные.

2. Найдем частное решение неоднородной системы методом подбора. Вектор-функция правой части системы Сопоставим ее с общей формой записи 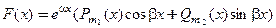. Ясно, что Можно принять, что 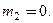Тогда . Так как является корнем характеристического уравнения кратности один, то частное решение следует искать в виде

(7)

Подставим частное решение в неоднородную систему и получим:

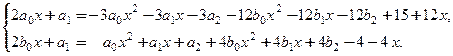(8)

Из условия равенства коэффициентов при одинаковых степенях х составляем систему шести линейный алгебраических уравнений относительно шести неизвестных коэффициентов. Первые два уравнения получены из условия равенства коэффициентов при в первом и втором уравнениях системы (8), следующие два уравнения − из условий равенства коэффициентов при 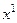, последние два содержат условия равенства свободных членов:

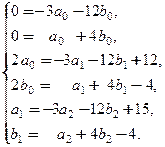(9)

Первые два уравнения пропорциональны. Значит, одно из этих уравнений можно отбросить, например, первое, при этом число уравнений − пять − становится меньшим числа неизвестных − шесть.

Составим два дополнительных полезных уравнения. Умножим 4-е уравнение системы (9) на число 3 и сложим со 3-м уравнением, аналогично 6-е уравнение умножим на 3 и сложим с 5-м:

(10)

Тогда 2-е уравнение системы (9) и 1-е уравнение системы (10) образуют систему имеющую только тривиальное решение Подставим эти числа в (9) и получим:

(11)

Снова коэффициенты в первых двух уравнениях пропорциональны. Значит, можно оставить только второе из этих двух уравнений как более простое. Рассмотрим систему, образованную 2-м уравнением системы (10) и 2-м из системы (11):

Подставим в (11). Последние два уравнения этой системы можно записать так:

В третий раз получены уравнения с пропорциональными коэффициентами, но в отличие от предыдущих случаев система − неоднородная, а решений − бесконечное множество:

В итоге, решение системы (9) имеет вид: − свободная переменная.

Если положить то получим

Таким образом, одно из частных решений неоднородной системы имеет вид:

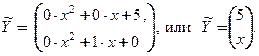(12) 3. Складываем (6) и (12) и получаем общее решение неоднородной системы:

Заметим, что метод сведения системы к дифференциальному уравнению здесь реализовался бы намного проще по сравнению с использованным методом подбора. ■

Пример 2. Решить систему дифференциальных уравнений

□ Данная система является неоднородной системой 2-го порядка с постоянными коэффициентами и специальной правой частью. Применим алгоритм 8.4.

1. Однородная система отвечающая данной неоднородной, решена в примере 1:

2. Найдем частное решение методом подбора. В правой части системы вектор-функция: Ее характеризуют такие параметры: Дополнительные параметры частного решения равны: 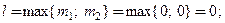, так как число не является корнем характеристического уравнения, отсюда . По формуле (4) частное решение неоднородной системы равно

, или (13)

Подставим (13) в неоднородную систему: 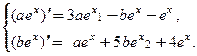Упростим:

Итак,

3. Общее решение неоднородной системы . Подставим вектор-функции, найденные в п.п.1, 2: ■

Метод вариации произвольных постоянных (метод Лагранжа)

Рассмотрим линейную неоднородную систему n -го порядка с коэффициентами , являющимися действительными функциями переменной х:

. (14)

Пусть вектор-функции образуют ФСР соответствующей ЛОСУ n -го порядка. Тогда согласно методу вариаций произвольных постоянных решение ЛНСУ представимо в виде

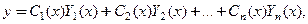(15)

где − неизвестные наперед функции, удовлетворяющие системе уравнений:

. (16)

Последующие действия повторяют процедуру решения линейного неоднородного уравнения методом вариации. Систему (16) можно рассматривать как систему линейных алгебраических уравнений относительно производных . Система имеет единственное решение, так как ее определитель равен определителю Вронского, который отличен от нуля в силу фундаментальности набора . Решая систему, найдем , а затем, интегрируя найденные выражения для производных, найдем и сами функции . Подставим их в (15) и получим решение.

Метод вариации произвольных постоянных позволяет построить как частное, так и общее решение линейной неоднородной системы. Если постоянным придать конкретные числовые значения, то при интегрировании выражений для производных по формуле (15) получим частное решение. Если постоянные не фиксировать, то формула (15) даст общее решение.

Пример 3. Решить систему дифференциальных уравнений методом Лагранжа:

□ Данная система решена в примере 2 методом подбора. Следуя заданию, решим ее методом Лагранжа − методом вариации произвольных постоянных.

Из примера 1 следует, что фундаментальная система решений однородной системы равна 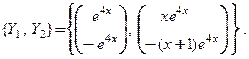Представим решение неоднородной системы в виде где − решения системы (16):

Найдем . Для этого разделим уравнения системы на 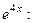Сложим уравнения системы и получим: Подставим в систему и получим Значит:

Функцию найдем при помощи формулы интегрирования по частям:

Функцию найдем, непосредственно интегрируя выражение для ее производной: .

Функци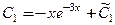и и подставляем в решение: 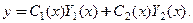Отсюда

, или

Общее решение системы получено методом Лагранжа. ■

Не нашли, что искали? Воспользуйтесь поиском: