Анализ изменения давления в цилиндре насоса в период нагнетания

Рассмотрим процесс нагнетания жидкости одноцилиндровым насосом одинарного действия в нагнетательную линию длиной l _н диаметром d _н (рис. 10). Ось цилиндра насоса расположена горизонтально, геометрическая высота нагнетания равна z _н, перекачиваемая жидкость имеет плотность ρ. Пусть в конце нагнетательного трубопровода поддерживается постоянное давление p _к.

Запишем уравнение Бернулли для сечений 2–2 и 3–3:

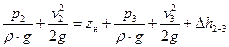, (39)

где р ₂= р _ц – давление жидкости в цилиндре насоса; v ₂= v _п – скорость движения жидкости в цилиндре, равная скорости перемещения поршня; р ₃= р _к – давление жидкости в конце нагнетательного трубопровода; v ₃= v _к – скорость движения жидкости в конечном сечении нагнетательного трубопровода; 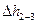– потери напора между рассматриваемыми сечениями 2-2 и 3-3.

Перепишем уравнение (39) с учетом приведенных замечаний:

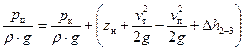. (40)

Потери энергии 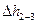между сечениями 2-2 и 3-3 состоят из потерь в местных сопротивлениях нагнетательного трубопровода, потерь по длине 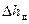и потерь на преодоление сил инерции в цилиндре 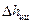и в трубопроводе .

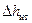При этом учтем, что потери в нагнетательном клапане изменяются аналогично потерям во всасывающем клапане, поэтому выделим эти потери в виде отдельного слагаемого. Тогда местные потери представим в виде:

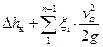= , (41)

где 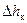– потери напора в нагнетательном клапане; – скорость движения жидкости в i -м участке нагнетательного трубопровода; 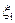– коэффициент местных потерь i -го местного сопротивления нагнетательного трубопровода.

Выразив в уравнении (41) скорость движения жидкости в трубопроводе через скорость поршня, получим:

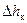= + , (42)

где 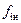– площадь поперечного сечения i- го участка нагнетательного трубопровода.

Потери напора по длине 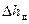нагнетательного трубопровода, состоящего из j участков длиной l_{j н} с диаметрами d_{j н} площадью поперечного сечения f_{j н} как и ранее, вычислим по известной формуле Дарси-Вейсбаха:

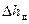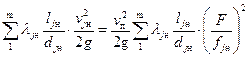= , (43)

где λ_{j н} – коэффициент гидравлического трения на j- м участке.

С учетом отмеченных замечаний и обозначений, уравнение (40) примет вид:

. (44)

Выражение, стоящее в квадратных скобках представляет собой сумму потерь в местных сопротивлениях и потери по длине. Выполнив преобразование этого выражения, получим:

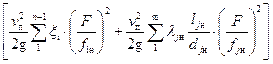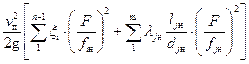
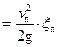= , (45)

где – приведенный коэффициент гидравлических сопротивлений нагнетательного трубопровода.

Подставим в уравнение (44) уравнение (45) и выразим скорость движения жидкости v _к в конечном сечении нагнетательного трубопровода через скорость поршня:

(46)

Потери напора на преодоление сил инерции жидкости в цилиндре вычислим по формуле:

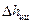
. (47)

Аналогично вычислим потери напора на преодоление сил инерции жидкости в нагнетательном трубопроводе:

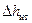
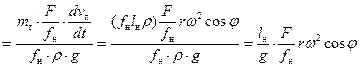. (48)

Для исключения из уравнений (25), (26) и (27) тригонометрических функций, воспользуемся уравнением (8) из которого выразим cos φ, а затем – sin φ:

cos φ 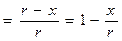. (28)

. (29)

Подставив выражение (29) в уравнения (25), а (28)– в уравнения (26) и (27), получим:

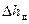+ = . (30)

. (31)

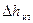
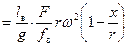. (32)

Не нашли, что искали? Воспользуйтесь поиском: